引言
在小学与初中教育的衔接阶段，数学作为一门逻辑性强、抽象程度高的学科，其教学方法的有效性与学生思维能力的培养密切相关。尤其在小学高年级阶段，学生正处于由具体形象思维向抽象思维过渡的关键时期，如何帮助他们顺利跨越这一门槛，成为小初衔接教育的重点之一。几何直观思想作为数学教学中的一种重要策略，通过数与形的有机结合，不仅能够帮助学生将抽象的数学概念具体化、形象化，降低学习难度，还能培养他们的逻辑思维能力和创新能力，为初中阶段的数学学习奠定坚实基础。因此，在小初衔接视域下，探索小学几何直观思想的教学策略具有重要意义。
一、小初衔接视域下的小学几何直观思想教学的现状
1. 教学模式单一固化：束缚思维之翼的枷锁
在小学数学的殿堂里，传统教学模式如同一道既定的轨迹，引领着无数师生穿梭于公式与定理之间。然而，这份“稳定”背后，却隐藏着对学生创新思维与探索精神的忽视。教师往往侧重于将数学知识以文字形式灌输给学生，课堂成了知识传递的单行道，而非思维碰撞的火花场。这种单一固化的教学模式，让学生如同被束缚了翅膀的鸟儿，难以展翅高飞，去探寻数学世界的广阔与深邃。数学，本应是一门充满逻辑美与创造力的学科，但传统的填鸭式教学却让学生陷入了机械记忆的泥潭。学生们被迫记住一个个公式、定理，却鲜有机会去理解它们背后的逻辑与联系，更谈不上将所学知识应用于解决实际问题。长此以往，不仅学生的数学学习兴趣逐渐消磨殆尽，更重要的是，他们的思维能力、创新能力也在无形中受到抑制。因此，打破传统教学模式的桎梏，探索多元化、互动性的教学方式，成为提升小学数学教育质量的关键。通过引入项目式学习、游戏化教学等创新手段，让学生在实践中学习，在探索中成长，才能真正激发他们的数学潜能，培养他们的综合素养。
2. 几何直观思想应用不足：错失直观理解的桥梁
几何直观，是数学学习中一座连接抽象与直观的桥梁。然而，在部分小学数学课堂上，这座桥梁却常常处于闲置状态，未能充分发挥其应有的作用。教师们往往过分依赖于文字描述和逻辑推理，而忽视了图形在解释数学概念、解决数学问题中的独特优势。图形，以其直观、形象的特点，能够帮助学生更好地理解抽象的数学概念。例如，在三年级学生第一次认识分数时，借助长方形、正方形、圆等平面图形的折一折、涂一涂、看一看，学生可以更直观的认识几分之一、几分之几，理解分子、分母以及分数的意义。又如，在学习运算律时，如下这些线段图、示意图，也可以帮助学生更容易去理解加法交换律、乘法分配律。
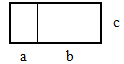
然而，由于几何直观思想应用不足，这些宝贵的教学资源往往被白白浪费。因此，加强几何直观思想在小学数学教学中的应用，是提高学生数学理解能力的重要途径。教师们应该充分认识到图形在数学教学中的重要作用，积极引导学生运用图形来辅助思考，使抽象的数学概念变得具体可感，从而激发学生的学习兴趣，提高他们的学习效率。
3. 学生抽象思维能力薄弱：亟待培养的宝贵财富
小学生的抽象思维能力尚处于发展阶段，这是他们面对数学学习时面临的一大挑战。然而，传统的数学教学往往忽视了这一特点，未能给予学生足够的支持和引导，导致他们在面对抽象的数学概念时感到困惑和无助。抽象思维能力，是数学学习中不可或缺的一项能力。它不仅能够帮助学生更好地理解数学概念和定理，还能够培养他们的逻辑思维和创新能力。然而，由于小学生的抽象思维能力相对薄弱，他们往往难以直接理解那些高度抽象化的数学知识。因此，教师需要采取有效的教学策略，逐步引导学生建立抽象思维框架。几何直观思想，就是培养学生抽象思维能力的一种有效手段。通过图形的辅助，学生可以更直观地理解数学概念，从而逐步建立起对抽象概念的感性认识。同时，教师还可以结合具体的生活实例和实际问题，引导学生运用所学知识进行思考和解决，进一步锻炼他们的抽象思维能力。
二、小初衔接视域下的小学几何直观思想教学的价值
几何直观思想的深远价值在数学的浩瀚宇宙中，就如同一颗璀璨的星辰，不仅照亮了学生们的学习之路，更在无形中塑造着他们的思维品质与综合能力。以下，我们将从降低学习难度、培养逻辑思维能力以及促进全面发展三个方面，深入探讨几何直观思想的深远价值。
1. 提高学习兴趣
数学，常因其抽象性而让部分学生望而却步。然而，几何直观思想的引入，如同为这道难题找到了钥匙。它将原本晦涩难懂的数学概念转化为生动直观的图形，使得复杂的问题变得简单明了。学生们在图形的辅助下，能够更容易地理解数学概念的本质，掌握解题技巧。这种“化繁为简”的能力，不仅降低了学习难度，更激发了学生们的学习兴趣。当学生们发现数学不再是遥不可及的抽象符号，而是可以通过图形这一直观工具来探索时，他们对数学的好奇心和求知欲便油然而生。
2. 培养逻辑思维能力
逻辑思维能力是数学学习的核心能力之一，也是未来社会所需的重要素质。几何直观思想在解题过程中，要求学生将数与形相结合，通过图形的变换和推理来解决问题。这一过程不仅锻炼了学生的空间想象能力，更培养了他们的逻辑思维和推理能力。学生们在图形的引导下，学会了如何有条理地分析问题、寻找规律、提出假设并验证结论。这种科学的思维方式和解题方法，不仅在数学学习中大有裨益，更将伴随他们一生，成为他们解决问题、创新创造的强大武器。
3. 促进全面发展
几何直观思想的价值远不止于数学学科本身。它如同一座桥梁，连接着数学与其它学科，也连接着学生的知识与能力、情感与态度。几何直观思想的引入，促进了跨学科的学习。在物理、工程等领域，几何直观同样发挥着重要作用。学生们通过几何图形来理解力的分解、运动的轨迹等物理概念，使得抽象的物理规律变得形象易懂。在工程设计中，几何直观帮助学生们更好地理解结构设计，提高设计的合理性和创新性。在几何直观的教学过程中，学生们需要观察图形、分析数据、提出假设、验证结论，这一系列活动不仅锻炼了他们的观察力、想象力和创造力，还培养了他们的合作精神、沟通能力和解决问题的能力。
三、小初衔接视域下的小学几何直观思想教学的策略
1. 更新教学观念，融入几何直观思想
在教育领域持续革新的今天，传统的教育视角已难以全面满足学生的多元化需求。因此，教师必须勇于革新教育观念，积极引入几何直观的教学理念。几何直观，简而言之，就是通过图形、图像等直观元素，帮助学生将抽象的数学概念具象化，从而提升理解深度。
首要的是，教师需致力于提升学生的空间认知能力。可以通过引入三维模型和图形来帮助学生更好地理解几何概念。例如，在讲解立体几何时，教师可以利用橡皮泥、积木或其他可操作的教具，让学生亲手构建几何体，从而直观地感受空间结构。其次，教师可以设计一些富有挑战性的空间推理游戏和活动，激发学生的兴趣。又如，通过拼图游戏、迷宫解谜等互动方式，让学生在玩乐中锻炼空间想象力和逻辑思维能力。其次，实践是学习几何不可或缺的一环。教师应鼓励学生亲手绘制图形、制作几何模型，通过亲身实践来深化对几何图形的认识。甚至还可以鼓励学生参与实际的建筑和设计项目，将理论知识应用于实践中。例如，让学生设计一个小型的花园或模型房屋，从规划布局到具体实施，这不仅能提高他们的空间认知能力，还能培养他们的创造力和团队合作精神。
2. 充分利用多媒体资源展开几何直观教学
前文写到：在小学数学教学中，几何直观教学尤为关键，因为它帮助学生形成空间观念，理解抽象的几何概念。而多媒体资源的引入，使得这一过程变得更加生动和直观。例如，在讲解“对称”这一概念时，可以通过动画展示一个图形如何通过轴对称或中心对称变换到另一个图形。学生通过观察动画，能够直观地理解对称的含义，而不仅仅是通过静态的图片或文字描述。其次，交互式电子白板和几何软件的使用，为学生提供了动手操作的机会。在课堂上，教师可以引导学生通过电子白板上的几何工具，亲自绘制和变换图形。例如，在学习“平行四边形”的性质时，学生可以在电子白板上拖动顶点，观察平行四边形如何在保持对边平行的情况下变形。这种互动式的学习方式，不仅提高了学生的参与度，还加深了他们对几何概念的理解。此外，利用虚拟现实（VR）技术，可以带领学生进入一个三维的几何世界。在虚拟环境中，学生可以“走进”几何图形，从不同的角度观察和探索。例如，在学习立体图形时，学生可以“进入”一个立方体，从内部观察各个面和顶点的关系。这种沉浸式的学习体验，使得抽象的几何知识变得具体而生动。最后，多媒体资源还可以用于创建丰富的几何游戏和练习。通过游戏化的学习，学生可以在轻松愉快的氛围中巩固所学知识。例如，设计一款拼图游戏，让学生通过拼凑不同的几何图形来完成任务。这种游戏不仅锻炼了学生的空间想象力，还激发了他们解决问题的兴趣。
3. 引导学生自主探究，培养几何直观思想
教师可以设计富有挑战性的几何问题，鼓励学生通过动手操作和实验来寻找答案。例如，可以利用几何拼图、几何积木等教具，让学生在拼接和组合的过程中，直观地感受几何图形的性质和关系。通过这种互动式的学习方式，学生不仅能更好地理解几何概念，还能培养他们的空间想象能力和逻辑推理能力。教师还可以鼓励学生进行小组合作学习。在小组讨论和合作的过程中，学生可以相互交流思路，共同探讨问题的解决方法。这种合作学习不仅能增强学生的团队协作精神，还能帮助他们从不同的角度理解几何问题，从而培养他们的几何直观思想。教师还应当注重培养学生的几何直观表达能力。在课堂上，教师可以引导学生用图形、符号和文字等多种方式表达自己的几何思想。例如，在解决几何证明题时，教师可以要求学生用图形来展示证明过程，用符号语言来表达逻辑关系，用文字来解释思路和方法。通过这种多维度的表达方式，学生不仅能更清晰地展示自己的思维过程，还能进一步巩固和深化他们的几何直观思想。
综上所述，小初衔接视域下的小学几何直观思想教学具有重要的现实意义和深远影响。通过更新教学观念、充分利用多媒体资源以及引导学生自主探究等策略的实施，我们能够有效地提升小学数学教学的质量和效果，为学生的全面发展奠定坚实的基础。
参考文献：
1. 张华, 李明. 数形结合思想在小学数学教学中的融合策略[J]. 数学教育学报.2023:34(2), 56-61.
2. 王丽, 刘强. 小初衔接阶段数形结合思维培养的实践研究[J]. 中小学数学教学与研究.2022: (8), 23-27.
3. 赵敏, 陈浩. 数形结合思想在小学高年级数学教学中的应用探索[J]. 教育导刊.2021: (11), 65-68.
4. 李芳, 王刚. 基于数形结合思想的小学数学创新教学策略研究[J]. 基础教育论坛.2020: (12), 34-38.