一、引言
材料在非对称应力循环下将产生循环塑性变形累积现象,这种现象称为棘轮效应。由于塑性变形的累积而使结构提前失效已经引起国内外学者的广泛关注。一直以来,国内外学者对各种材料的棘轮行为进行了大量研究,取得了一定的成果[1-7]。然而,对铝合金等材料的棘轮行为研究很少[8-9],而已有的研究表明[10],材料不同,所表现出的棘轮行为及时间相关性也不同。因此,有必要进一步对铝合金材料的棘轮行为进行研究。
7050铝合金属高强度可热处理合金,具有极高的强度及抗剥落腐蚀和抗应力腐蚀断裂的性能。常用于飞机结构件、自由锻打件与模锻件。因此,对7050铝合金材料进行棘轮行为的研究具有重要的实际意义。本文将对7050铝合金材料室温下的单轴棘轮行为及时间相关性进行实验研究,讨论室温下材料的棘轮行为及时间相关性,为以后的航空产品的设计选材提供丰富的理论和实验基础。
二、实验方法
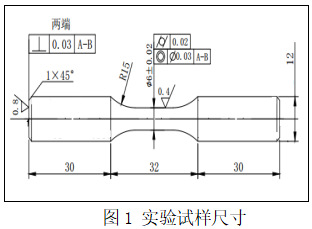
实验材料为7050铝合金板材,其化学成分(质量分数/%)为:Si-0.03, Fe-0.07,Cu-2.3,Mg-2.2,Mn-<0.1,Zr-0.11,Cr-0.01,Zn-6.3,Ti-0.05,其他单一<0.05,其他总和-<0.15,其余为Al。所有实验都采用同一种实心圆棒,取样方向为板材的纵向,试样形状和尺寸如图1所示。实验设备为MTS370.10电液伺服控制试验机。实验数据通过安装在等直段上标距为12 mm的引伸计测量,并采用FlexTest 40控制系统进行闭环控制和数据采集。在室温下应力控制的实验中,如无特别说明,加载应力率都为,300 Mpa/s,应变控制的实验中,加载应变率都为0.004/s,所有实验的加载波形都采用三角波。
三、结果与讨论
首先,为了了解7050铝合金材料的基本力学性能,对材料做了两个不同加载应变率下的单拉实验,为循环变形实验工况的设计提供参考。图2为0.000 2/s和0.002/s两个不同应变率下的应变控制的单拉曲线(单轴拉伸实验只做到了7%的应变),基本的拉伸性能如表1,可见在弹性阶段,应变率对材料的单拉性能几乎没有什么影响,而在塑性阶段,有一定的影响,应变率越大硬化越大,但整体差别不是很大。并且它们的硬化程度都不是很大。
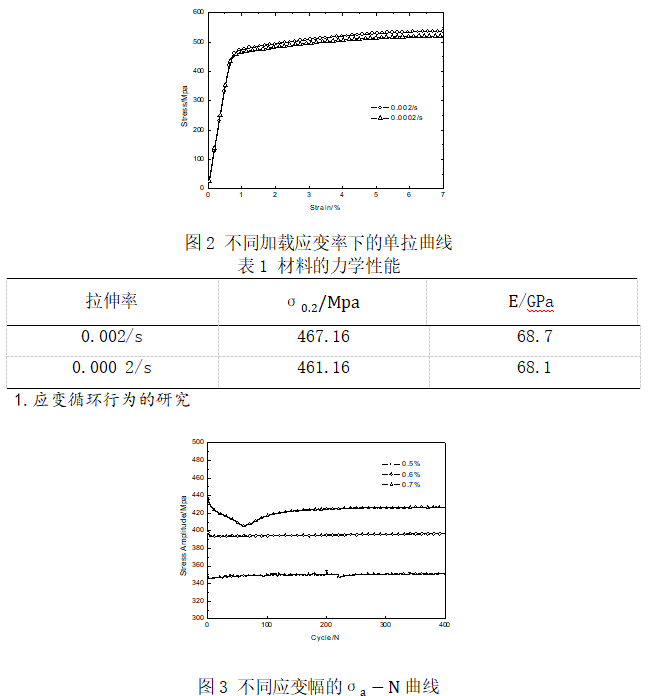
首先,对7050铝合金材料进行了不同应变幅值的对称循环应变实验研究,揭示不同应变幅下响应应力幅的变化情况,实验结果如图3所示。从图中可知,响应应力幅值随着应变幅值的变大而增加,在较大的应变幅值下(0.7%),刚开始响应应力幅值随着循环周次的增加而快速减小,但几十个循环后达到稳定,材料表现出先弱化后稳定的特性;较小应变幅值下(如0.5%),响应应力幅值在整个循环过程中基本没有变化,材料表现循环稳定特性;在应变幅值0.6%下,响应应力幅值随着循环周次的增加而变小,但在几个循环后很快达到稳定。由此可见,材料在较大应变幅值下,随着循环周次的增加响应应力幅值变小,但很快达到稳定;在在较小应变幅值下,随着循环周次的增加响应应力幅值基本不变。
2.棘轮应变及时间相关性
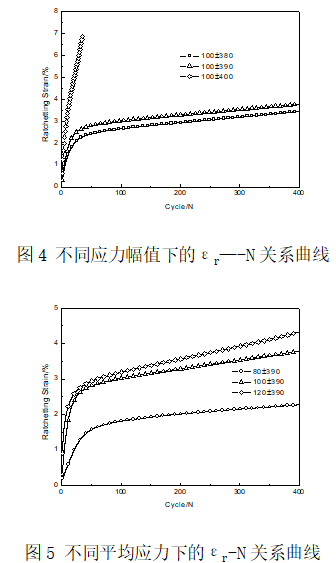
研究平均应力和应力幅值对材料的棘轮变形行为的影响,分别进行了平均应力相同应力幅值不同和平均应力不同应力幅值相同的实验。图4给出了平均应力均为100 MPa,应力幅值为380 MPa、390 MPa和400 MPa三种工况下的实验结果,从图可以看出,在平均应力相同时,棘轮应变率随着应力幅值的增加而变大,棘轮应变达到一定值后,棘轮应变率快速增加,直到最后的破坏。在380Mpa和390Mpa工况下,棘轮效应变化不是很大,但在400Mpa工况下,棘轮效应成指数增加,40多个循环之后材料发生快速断裂,说明在400Mpa工况下是材料的一个临界点。图5给出了应力幅值均为390 MPa,平均应力为80 Mpa、100 MPa和120 MPa两种工况下的实验结果,图中的结果也反映了相同的棘轮应变演化特点,即应力幅值相同时,棘轮应变率随着平均应力的增加而变大。
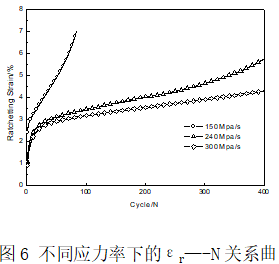
为了揭示棘轮应变的时间相关特性,在工况(120±390 Mpa)下,进行了应力率分别为150 MPa/s、240 MPa/s和300 MPa/s的应力控制的循环实验。结果如图6所示。由图所示,不同加载应力率下的棘轮演化规律相同,都是随着循环的进行,棘轮应变率减小,棘轮应变达到一定值后,棘轮应变率快速增加,直到最后的破坏。但棘轮应变率随着加载率的减小而增加,说明加载率对棘轮应变的产生有很大的促进作用。
四、结论
(1)响应应力幅值随着应变幅值的变大而增加,在较大的应变幅值下(0.7%),刚开始响应应力幅值随着循环周次的增加而减小,但很快达到稳定,较小应变幅值下(如0.5%),响应应力幅值随着循环周次的增加而基本保持不变,材料表现循环稳定特性。
(2)平均应力相同时,棘轮应变率随着应力幅值的增加而变大。应力幅值相同时,棘轮应变率随着平均应力的增加而变大。
(3)同一工况下,不同加载应力率下的棘轮演化规律相同,但棘轮应变率随着加载率的减小而增加,说明加载应力率对棘轮应变的产生有很大的促进作用。
参考文献
[1]蔡力勋,罗海丰,高庆.用于棘轮变形预测的棘轮演化统一模型研究[J].航空学报,2002,23(1):17-22.
[2]刘宇杰,蔡力勋,杨显杰,等.描述1Cr18Ni9Ti不锈钢单轴棘轮行为的黏塑性本构模型[J].ACTA AERONAUTICA ET ASTRONAUTICA SINICA,2005.
[3]Kang G.A visco-plastic constitutive model for ratcheting of cyclically stable materials and its finite element implementation[J].Mechanics of materials, 2004, 36(4): 299-312.
[4]杨显杰,高庆.紫铜的循环棘轮行为研究[J].西南交通大学学报,1997,32(6):604-610.
[5]Chen X, Jiao R, Kim K S.On the Ohno–Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel[J].International Journal of Plasticity, 2005, 21(1): 161-184.
[6]康国政,高庆.不同材料的室温单轴应变循环特性和棘轮行为研究[J].机械强度,2002,24(4):608-612.
[7]康国政,孙亚芳,张娟,等.SS304不锈钢在室温单轴循环加载下的时相关棘轮行为[J].金属学报,2005,41(3):277-281.
[8] 丁俊, 康国政, 刘宇杰, 等. 6061-T6 铝合金单轴时间相关循环变形行为[J]. 中国有色金属学报, 2008, 17(12): 1993-1998.
[9]丁俊,康国政,刘宇杰.LY12CZ铝合金材料的室温和高温单轴循环变形行为及其时间相关性[J].航空学报,2008,29(1):70-74.
[10]Yang X J, Chow C L, Lau K J.Time-dependent cyclic deformation and failure of 63Sn/37Pb solder alloy[J].International Journal of Fatigue, 2003, 25(6): 533-546.
