本文所研究的球形十二足对称机器人包含一个位于正十二面体体心的用来安装12条伸缩腿的质量均匀分布的球形中间基座和十二条伸缩腿，每条伸缩腿首端位于正十二面体的体心，末端位于正十二面体正五边形面的面心。为对球形十二足对称机器人进行动力学建模，将机器人简化为单刚体，质心位于中间基座的球心上，12条伸缩腿相对于中间基座的位置固定。由于伸缩腿相对于中间基座的位置固定，在机器人运动过程中，计算出中间基座的位置坐标及姿态角，即可得到十二条伸缩腿的方位，再结合地形信息即可得到每条伸缩腿的长度。

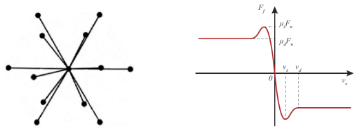
图1 球形十二足对称机器人示意图 图2 STEP函数表示的摩擦力

采用如下的广义坐标对球形十二足对称机器人进行动力学建模：

(1)

公式（1）中，[x y z]^T为机器人质心在惯性坐标系中的位置，[v_x v_y v_z]^T为质心在惯性坐标系中的速度，[λ₀ λ₁ λ₂ λ₃]^T为表示随体坐标系机器人姿态的欧拉参数，[ω_x ω_y ω_z]^T为机器人中间基座转动角速度在随体坐标系下的三个分量。对机器人质心位置坐标求导有：

(2)

对机器人质心速度求导有：

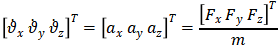(3)

公式（3）中，[x y z]^T为作用在机器人质心的外力之和，包括地面接触力、重力等，忽略空气阻力的等较小的外力，其中重力的大小和方向都与机器人运行的实际环境一致，可以地面的重力也可以根据所探索的小行星的引力进行对应的设置。对描述机器人姿态的四元数求导可得:

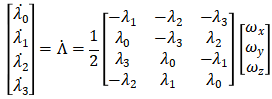(4)

根据动量矩定理，机器人质心的角速度导数可以表示为：

(5)

因为机器人已经简化为质量均匀分布的中间基座（实心球）上，所以J在坐标轴三个方向上对应的主惯性矩相等，因此公式（5）在随体坐标系下的投影式为：

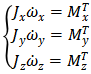(6)

公式（6）中，J为随体坐标系中的转动惯量，M^T为随体坐标系下的外力矩，忽略空气阻力等较小的外力，该力矩主要是地面接触力向质心简化得到的。地面接触力主要包括地面给机器人的支持力和切向摩擦力，因此只要计算这两个力，就可以计算得到球形十二足对称机器人的动力学方程。

计算地面支持力时，将机器人的伸缩腿视为可以控制长度变化的无质量的杆，伸缩腿末端为质量很小的小球，将地面视为弹簧阻尼装置，采用Kelvin-Voigt模型。

(7)

公式（7）中，δ为伸缩腿末端在地面法相方向上嵌入地面的深度，为伸缩腿末端在地面法向方向上的速度，K为地面刚度系数，根据地面参数进行选取，D为接触阻尼系数。第i条伸缩腿嵌入地面的深度δ_i的值可通过伸缩腿末端球的半径r和球心的z的坐标z_ui来计算，当r-z_ui<0时，δ_i=0；当r-z_ui>0时，δ_i；相应的δ_i=r-z_ui的值为伸缩腿末端球球心ui在z轴方向上速度的大小。

在计算地面对机器人切向摩擦力时，采用修正的库仑摩擦模型，如公式（8）所示，其中相对切向速度为伸缩腿末端球球心在x，y平面内的速度。

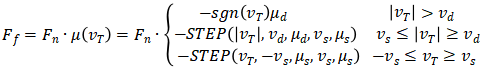(8)

公式（8）中，v_T为接触两物体的相对切向速度，μ_d和μ_s分别为动摩擦系数和静摩擦系数，v_d和v_s分别为动静摩擦转换的相对切向速度；STEP函数如图2所示。

本文采用牛顿-欧拉方法建立球形十二足对称机器人的动力学模型，并考虑了机器人与地面的接触力。通过所建立的动力学模型可进行动力学仿真，进而研究球形十二足对称机器人的步态规划和运动规划。

参考文献

[1]刘延柱,潘振宽,戈新生.多体系统动力学[M].北京:高等教育出版社,2014.

[2]杨顿,杨帅,于洋等.基于深度强化学习的复杂地形适应机器人设计与实验[J].宇航学报,2022,43(09):1176-1185.