1研究背景
近些年来，风力发电实现了迅猛发展，电力能源中其占比呈逐年增大的趋势。现阶段，在进行风力发电时通常会使用双馈型风力发电机。该设备的异构电源形式有别于同步发电机，随着该设备的大规模接入，网损、电网节点电压、线路功率等备受影响。与此同时，在结构特点上，其和同步发电机也存在差异，其不可采取传统的潮流计算方法。所以，此次研究中将进一步分析研究大规模双馈型风力发电机接入电网后的潮流计算方法，对工程实践具有十分重要的意义。
一般而言，在实施光、风等新能源电力系统的潮流计算的过程中会直接把多种新能源当成PQ节点，选择牛顿-拉弗森法方法进行潮流计算。以各类新能源为PV节点，选取生顿-拉弗森法方法计算潮流；然而此计算方式未将不同种新能源的控制方式以及电磁特征纳入到思量范围内，仅仅是浅显地将各类新能源变为PQ节点或PV节点，此法求出的电网潮流有明显误差。采用新能源建模，以电源并网点的电流或者电压求算需迭代的节点功率。迭代时一般要把分布式电源当成PQ节点，选择前推回代法予以潮流计算。有别于牛顿-拉弗森法的是，此法对存在多个弱环与电源的配电网根本不适用。把双馈型风力发电机看作是P-Q(V)节点，却不注重风力发电机控制策略和输出功率之间的关系。
针对前文提及的问题，笔者深入探究了双馈型风力发电机的电磁特征，并系统思量正常运行状态下对风机的控制方式，以就双馈型风力发电机的电力系统潮流计算方式给出合理建议。在牛顿-拉弗森法的基础上，把双馈型风力发电机视为P-Q(V)节点，以期能够促使大规模风电接入后的电力系统潮流计算的精准度得到有力提升。
2 双馈型风力发电机电磁特性
结合正常运行状态下双馈型风力发电机的电磁耦合特性可知，可以以下公式反映转子绕组的电磁关系：
式中:Ur,为转子电压矢量;I2为转子电流矢量;r2为转子绕组电阻;x2为转子绕组漏抗;E2为转子侧感应电动势矢量。
考虑到双馈型风力发电机的转子与定子在电流频率、电压上存在差异，为明晰双馈型风力发电机的电磁耦合特性，有必要进一步转换转子频率。经过前文研究发现，频率变频转换的前提是等效的静止转子满足120=I2,这一条件。也就是说，一个静止且电阻为r2/s的等效转子来表示电阻为r2的实际旋转转子，这一情况下转子侧电压可将其转化为Ur/s。基于对绕组的变比折算的考虑，得到了双馈型风力发电机的基本方程。在普通异步发电机的转子回路的基础上，双馈型风力发电机又新添了励磁电源Ur/s，也就是转子侧变流器。实践结果显示，确立并实施完善而又科学的转子侧变流器的控制方案，有助于改善双馈型风力发电机的输出特性。
由上可知，自双馈型风力发电机等效电路能获取到双馈型风力发电机的等效电路。
3 双馈型风力发电机调节作用
经过对传统绕线式发电机矢量图进行研究后发现，当处于正常运行状态下时，发电机参数与转率是已知的的话，那么意味着转子、定子的相位也是已定的。发电机一方面能将有功功率输出来，另一方面，能将一些无功功率充分吸收进来，实现电机励磁。
双馈型风力发电机接入转子励磁电压之后，定子的电流与电压的相位会出现较大改变。在此情况下，可考虑对转子励磁电压进行调整，从而得到想要获取到的发电机的功率因数，使双馈型风力发电机的运行特性得到明显优化。经过对双馈型风力发电机矢量图进行分析后发现，当处于超同步运行的状态中，转率在0以下时，双馈型风力发电机会将有功功率输入系统，同时还会将容性无功功率输入至系统内。
4 双馈型风力发电机控制策略
双馈型风力发电机的控制策略有许多可供选择，比方说直接功、矢量控制策略等。在这当中，矢量控制策略在双馈风力发电机组中得到了大范围地运用。鉴于其较强的鲁棒性，可以提高该发电机的运行性能，同时控制机组输出。
矢量控制模型指的是一种以感应异步发电机为基础，同处于同步旋转坐标系内的一种综合矢量模型。其内部的定子主磁链与同步旋转坐标系的d轴重合，同步旋转坐标系的q轴超前于d轴90，共同组建了定子磁链定向的同步旋转坐标系。
图1定子磁链定向同步旋转坐标系
如图1所示，s,abc为定子磁链综合矢量，us,abc为定子电压综合矢量，ws为定子转速。s,abc的d轴、q轴分量可表示为:
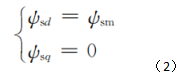式中:sm为定子主磁链幅值。
当忽略励磁电流时，输出的有功功率P和无功功率Q可表示为:
按照公式（3）不难发现，定子磁链定向综合矢量模型内，位于转子电流的q轴分量以及d轴分量都具备与之对应的双馈型风力发电机输出的有功功率与无功功率。因此，有必要对双馈型风力发电机转子侧变流器的控制系统进行规划设计。通过对电力系统关于风电场输出功率的要求进行分析后发现，可结合自身需要对无功功率指令值Qs,ref与有功功率指令值Ps,ref进行设定。同时，可考虑采取最大功率跟踪算法将风力发电机的转速指令值求出来，循序渐进，以求得双馈型风力发电机的有功功率指令值，按照机端电压指令值可以计算出无效功率指令值。
5 双馈型风力发电机PQ(V)节点处理
双馈型风力发电机和常规同步发电机异构的电源形式存在差异，考虑到机端电压与电机参数等所产生的影响，在进行潮流计算时指出要把双馈型风力发电机当成PQ（V）节点，从而系统地呈现出此发电机的输出特征。
对双馈型风力发电机的P-Q(V)节点进行处理的过程中，首先作个假设：双馈型风力发电机的功率解耦控制元件能发挥出无差异调节的作用，控制策略求出的转子电压指令值其实与双馈型风力发电机转子侧变流器实际输出的转子电压相等。
根据计算可推出双馈型风力发电机瞬时输出的无功功率，从而在潮流迭代过程中将该发电机从PV节点转换为可处理的PQ节点，机端定子电压U1的变化将决定无功输出功率Q。依照相关计算公式，可将双馈型风力发电机瞬时输出的无功功率求出来，以得到潮流迭代时
6潮流计算
按照前文提及的双馈型风力发电机P-Q(V)节点处理方式，利用牛顿-拉夫森法将电力系统潮流求出来，以下为详细的计算步骤：
（1）通过对网络数据进行收集与研究，选择把双馈型风力发电机当成P-Q(V)节点的形式保存起来，创立全网导纳矩阵，将各种节点电压的收敛精度与初值设置完毕。
（2）对双馈型风力发电机的P-Q(V)节点进行初始化处理，代入机端电压、感应异步发电机以及输出有功功率，以求得双馈型风力发电机输出的初始无功功率。
（3）将新能源并将网点的初始注入功率求出来，以步骤（2）获取到的结果求出并网点的实际初始注入。
(4)实施第k次迭代，采取生顿-拉弗森法将电压直角坐标系虚部偏差△f（k)以及第k次迭代后所有节点电压直角坐标系实部偏差 Δe(k）求出来，然后求得P-Q(V)节点的Q(k+1)，以完成对节点的注入功率的更新迭代。
7 算例分析
利用节点标准化测试系统进行研究与求算，该系统中有11个负荷与5台发电机，同时把节点1设定成平衡节点。
7.1节点3接入双馈型风力发电机
把节点3与依靠30台双馈型风力发电机组建起来的风电场相连，其共有45MW的总有功功率输出。通过运用上述计算方式，得出下表1所示的潮流。
表1 节点3接入双馈型风力发电机计算结果
基于节点标准化测试系统内部，节点3的节点电压标么值是1.01。把节点3与双馈型风力发电机相连接之后，节点3的电压标么值将发生变化，由1.01变为1.0376。从这不难发现，基于双馈型风力发电机控制策略的影响，电网的无功支撑效用比较强大。
7.2增加节点3双馈型风力发电机装机容量
增加节点3的双馈型风力发电机装机容量计算潮流之后，所得的结果详见下表所示：
表2 增加节点3双馈型风力发电机装机容量计算结果
利用表2的计算结果针对双馈型风力发电机的P-V以及P-Q曲线进行分析与研究。
通过对双馈型风力发电机基于控制策略的影响进行分析与研究后发现,其输出特性及其对系统的影响主要体现在：
(1)随着双馈型风力发电机的有功输出功率慢慢变大，机组输出的无功功率也会发生变化，呈先增后减的发展态势。通过对式（9）至（12）进行分析后发现，转差与机组参数影响无功功率的波动趋势。
(2)控制策略直接影响双馈型风力发电机的机端电压。基于机组控制模块的影响，机端电压的变化会在一定程度上令双馈型风力发电机自动调整无功功率的输出受到影响，使系统电压升高。
8 结束语
双馈型风力发电机电力系统的潮流计算，要求系统地思量风力发电机的控制策略以及电磁特性，以此对双馈型风力发电机为主要机型的风电场的输出特性作出系统描述。双馈型风力发电机不同于传统绕线式发电机，其借助转子侧变流器将转子励磁电压引进来，使其运行状态得到优化。如此，双馈型风力发电机既可以输出有功功率，并往系统输出容性无功功率，最终发挥出支撑电网电压的效能。控制策略直接影响双馈型风力发电机的机端电压，基于机组控制模块的影响，机端电压的变化会在一定程度上使双馈型风力发电机自动调整无功功率的输出受到影响。
参考文献：
[1]刘丰瑞,何雨哲,张琳,王帅.风电场环境下的电力系统潮流算法[J].通信电源技术,2019,36(01):66-67.
[2]周勃. 含双馈型风电场的电力系统无功优化策略研究[D].兰州理工大学,2017.
[3]曹政. 风电并网对电力系统调度运行影响的研究[D].山东大学,2016.
[4]赵宁,于少鹏.含风力发电机组电力系统潮流及稳定分析[J].产业与科技论坛,2015,14(22):75-76.
[5]丁宁. 大规模集群式风力发电系统潮流优化计算与故障分析[D].兰州理工大学,2014.