引言：企业材料采购问题是企业供应链管理研究的重要方向。企业生产经营过程中，对于原材料的采购，机器设备的添置，以及外部技术、服务的购买等生产经营行为，一般都涉及采购策略的问题。实际问题中，需要结合供应销的运营特点以服务供应商公司和客户，建立以总利润最大、总质量最高以及总消耗最小为目标的多目标优化模型。该文采用NSGA-Ⅱ算法进行求解模型，算例结果表明，多目标优化较单目标优化更具优势，它能够提供一个决策集合，决策者可以通过权衡比较，做出更有利于企业长久发展的决策。
一、背景
为了更好的说明该算法模型，作者带入某实际问题进行论述，引入背景如下。
某生产企业所用原材料可分为A，B，C三种类型。该企业每年按48周安排生产，需要提前制定24周的原材料订购和转运计划，即根据产能要求确定需要订购的原材料供应商和相应每周的原材料订购数量，确定第三方物流公司并委托其将供应商每周的原材料供货数量转运到企业仓库。
该企业每周的产能为2.82万立方米，每立方米产品需消耗A类原材料0.6立方米，或B类原材料0.66立方米，或C类原材料0.72立方米。供应商不能保证严格按订货量供货，为保证生产需要，该企业尽可能保持不少于两周生产需求的原材料库存量。每家转运商的运输能力为6000立方米/周，一般一家供应商每周供应原材料尽量由一家转运商运输。实际中A类和B类原材料的采购单价分别比C类原材料高20%和10%，三类原材料运输和储存单位费用相同。
二、建立多目标优化方程
为了减少原材料转运和仓储的成本，由于在实际生产过程中，每立方米产品A类原材料的消耗量比C类原材料的消耗量少0.12立方米，因此选择尽量多地采购A类和尽量少地采购C类原材料，同时在转运方面选择转运损耗率低的转运商。因此，本文将该问题看作一个多目标优化问题并建立带有精英策略的非支配排序的遗传算法模型（NSGA-Ⅱ）。
我们首先建立了三个目标规划，分别是：（1）要求A类原材料尽可能地多；（2）B类原材料尽可能地少；（3）购买成本最小，该购买成本只考虑原材料的成本。
给定决策向量
，它满足下列约束：
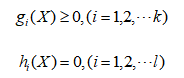
设有r个优化目标，且这个r优化目标是相互冲突的，优化目标可表示为
寻求
,使
在满足约束式的同时达到最优。
三、建立NSGA-Ⅱ算法模型
3.1NSGA-Ⅱ算法
遗传算法的基本思想是基于模仿生物界的遗传过程。该算法用基因表示问题的参数，用染色体表示问题的解，从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争，适者有最好的机会生存和产生后代，后代随机继承父代的最好特征，并重复这上述过程。群体的染色体不断进化，逐渐适应环境，最后收敛到该群体最适应环境的类似个体，即得到了问题得最优解。
3.2精英策略
扩大采样空间。将父代种群与其产生的子代种群组合，共同竞争产生下一代种群，有利于保持父代中的优良个体进入下一代，并通过对种群中所有个体的分层存放，使得最佳个体不会丢失，迅速提高种群水平。
3.3基于Pareto的多目标最优解集
在多目标优化问题中，由于是对多个子目标的同时优化，而这些被同时优化的子目标之间往往存在一定的冲突，对一个子目标进行优化往往会导致其他至少一个子目标恶化，因此，针对多目标优化问题，绝对最优解一般不存在。
Pareto最优解，一般地，可以描述如下：
给定一个多目标优化问题
，它的最优解X*定义为：
其中：
，Ω为满足问题的可行解集，即：
称Ω为决策变量空间，向量
将
映射到集合
，是目标函数空间。
3.4Deb的非支配排序方法
设进化群体为P，同时设置一个构造集P'，算法开始时将第一个个体放入构造集P中，一次将进化的群体P中的个体P(P￠P')取出并放入构造集P' 中，同时将当前取出的P依次与所有个体进行比较，删除P' 中所有被支配的个体，若个体P被P' 中的任意一个个体所支配，则将P从P' 中删除。
3.5拥挤度定义
拥挤度计算方式：令
。对于每个目标函数依次进行下列操作：（1）基于该目标函数对种群进行排序；（2）令边界的两个个体拥挤度为无穷，即；
；（3)计算
四、模型求解
根据上述基本原理建立NSGA-Ⅱ模型。根据对问题的分析，我们提出：
为第j家供货商在第i周拥有的供货量，其中：i=1,2,…24;j=1,2,…402。
为我们在第周向第家供货商是否提供订单，
=0,1；其中0表示我们在该周不向该供货商提供订单，1表示我们在该周向供货商提供订单。
表示第家供货商提供原材料的种类，
=1,2,3;其中1表示该供货商提供A类原材料，2表示该供货商提供B类原材料，3表示该供货商提供C类原材料。
为第i周的购买成本；
为第i周订购A类原材料的数目；
为第i周订购C类原材料的数目，则可以写出该问题存在三个目标函数(公式为第周)。
每周的购买成本应该尽量小：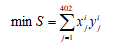
每周购买A类原材料尽量多：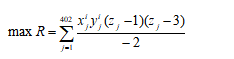
每周购买C类原材料尽量少：
存在一个约束条件且为不等约束条件，即每周的订货量转换为产能应大于2.82万立方米，即：
根据上述目标函数和约束条件运用matlab建立NSGA-Ⅱ模型求解，得到未来24周的订购方案。
参考文献
[1] 罗焕，闫富乾.基于变邻域NSGA-Ⅱ算法的多目标货位优化研究[J.]制造业自动化，2021，43(10):26-29+36
[2] 潘野，刘晓婷.改进的NSGA-Ⅱ算法的柔性物料搬运策略[J].科学技术与工程，2021，21(01):240-247
[3] 刘胜军，耿焕同，谢飞.新型定向交叉在NSGA-Ⅱ求解多目标TSP问题中的应用[J].电子技术与软件工程，2017，(06):154
