复合材料具有较高的比强度和比刚度，并且具有可设计性，现已广泛应用于航空航天等领域，且其应用范围已从起落架舱门、活动面等次承力结构逐步发展到盒段等主承力结构。梁腹板主要承受面内剪切载荷，失效模式为剪切屈曲失稳，目前通常使用的屈曲计算方法有工程算法和有限元方法，工程算法较为便捷，而有限元法应用范围更广。本文使用不同的计算方法，结合某型民机平尾盒段梁腹板剪切稳定性试验结果，对比分析各种方法的优劣。同时试验数据表明，试验件失稳后并不会立即发生破坏，仍然具有很强的后屈曲能力。
1剪切稳定性试验
1.1梁腹板试验件
梁腹板稳定性试验件选取某型民机平尾后梁典型参数部位，试验件由复材梁、复材支柱、金属支柱、金属蒙皮、加强板等组成，其中复合材料为单向带M21/34%/UD134/AS7和织物M21/40%/285T2/AS4C-6K，蒙皮模拟件及金属支柱采用7050-T7451，加强板采用30CrMnSiA。除复材支柱与梁腹板采取胶结连接外，其余部件采用螺栓连接。试验件考核区腹板厚度为1.908mm，支柱间距为154mm，高度为185mm，长度为918mm。试验件如图1所示，复合材料性能数据见表1。
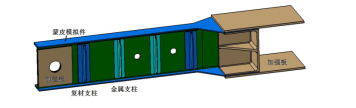
图1 试验件结构示意图
表1 复合材料性能
梁腹板及缘条铺层顺序为[(±45)/0/45/90/-45/0]s，共12层，厚度为1.908mm；支柱自由端铺层顺序为[(±45)/(0,90)/(±45)]s，共6层，厚度为1.854mm；支柱连接端铺层顺序为[(±45)/(0,90)/]s，共5层，厚度为1.545mm。其中，(±45)、（0,90）为AMMS3203 40型 285级，单层厚度0.309mm，其余为AMMS3202 34型 1类 134级，单层厚度0.129mm。
本次共选用3件完全相同的试验件，分别在梁腹板正面、背面、支柱、蒙皮模拟件上布置应变片，共计256片，其中考核区应变片序号如图2所示，腹板正面反面对称贴片，序号相同。
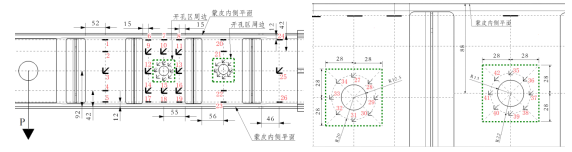
(a)正面贴片图 (b)开孔区周边贴片图
图2 试验件腹板贴片图
1.2 试验实施
如图3所示，试验采用悬臂梁式试验方案，试验件一端支撑在承力墙上，另一端施加试验载荷，加载点位于试验件的剪心，试验件上下分别用槽钢固定，上下槽钢用拉板连接。
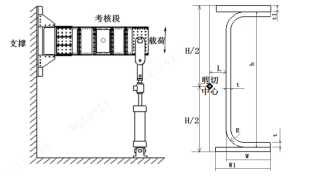
图3 梁腹板剪切稳定性试验加载、支持示意图
复合材料在重复载荷与环境暴露的影响下可能会引起材料性能的退化，为保证试验验证充分，本试验采用环境因子补偿方法，来确保环境暴露对静强度的影响。根据全机理论计算结果，筛选出试验件考核部位最大剪应变为1287，剪切弹性模量为20GPa，梁腹板厚度为1.908mm，高度为185mm，同时考虑1.15的环境因子，故试验载荷为10.465kN。
试验首先进行预试，加载至40%试验载荷后卸载，查看应变及位移数据，确保所有应变片及设备的有效性以及载荷的准确性；其次进行限制载荷试验，加载至67%试验载荷，保载30秒后卸载，根据腹板上应变片曲线判断试验件屈曲载荷及残余应变情况，并对试验件进行目视及无损检测；最后进行极限载荷试验，加载至100%试验载荷，保载3秒后若未破坏则继续加载直至试验件破坏，若加载至200%试验载荷，试验件仍未破坏，则试验停止。
1.3试验结果
所有试验件在完成限制载荷试验后，均未发生屈曲，在完成极限载荷试验后，试验件均未破坏，试验后无损检测均为发现异常。根据试验数据对比分析，加载至200%之前，试验件均已发生屈曲，试验曲线最早出现明显分叉的区域为孔的45度方向，此处应变花编号分别为32、40，载荷-剪应变曲线如图4所示。
(a)32号应变花剪应变
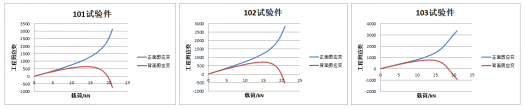
(b)40号应变花剪应变
图4 载荷-剪应变曲线
根据载荷-剪应变曲线可知，取应变曲线明显分叉处作为屈曲载荷，3个试验件屈曲载荷分别为13.81kN、15.07kN、13.29kN，平均值为14.06kN。
2 屈曲计算方法
2.1 工程分析方法
试验件剪切屈曲首先发生在梁腹板开孔处周边，梁缘条、蒙皮模拟件、支柱对梁腹板起支持作用，工程分析时，采用四边简直约束进行计算。
剪切屈曲计算公式为：
式中：
为单位长度上剪切临界载荷，N/mm；
；
为弯曲刚度系数，N·mm；
b为宽度（b≤a），mm；
试验件腹板弯曲刚度系数为
，b取支柱间距为152mm，经计算剪切屈曲载荷
=75.48N/mm。腹板高度为185mm，折算出试验件屈曲载荷为13.963kN。
根据对比试验结果可知，工程分析方法屈曲载荷值与试验结果相差0.68%。
2.2 有限元方法
分别采用有限元特征值分析法和弧长法对试验件屈曲载荷进行计算。采用MSC.Patran建立试验件有限元模型，试验件均简化为shell单元，连接件简化为beam单元，采用RBE2单元在加载端施加试验载荷，在试验夹具端部连接处进行约束。试验件考核区域单元尺寸约6mm，有限元模型示意见图5。
图5 有限元模型示意图
1.1.1 特征值分析法
选用MSC.Nastran进行屈曲分析，在加载端施加100%试验载荷，提交105屈曲模块进行求解。试验件的前4阶特征值及屈曲载荷见表2，屈曲最早发生于两个孔的45度方向，前4阶屈曲模态如图6所示。
表2 剪切屈曲特征值及屈曲载荷
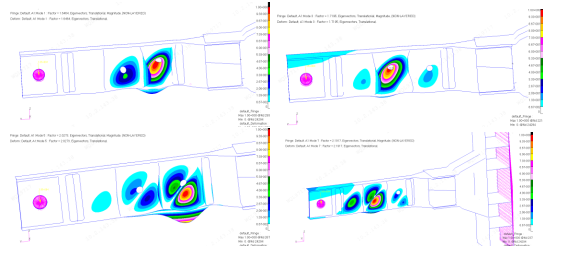
图6 前四阶屈曲模态
取第1阶特征值为试验件屈曲载荷，即17.23kN。根据对比试验结果可知，特征值分析法屈曲载荷值与试验结果相差22.56%。
1.1.2 弧长法
在有限元特征值分析方法的基础上，采用有限元弧长法对试验件进行剪切屈曲分析。根据特征值法分析得到的第一阶屈曲模态，将其乘以0.1作为初始缺陷引入屈曲分析模型中。施加200%试验载荷，采用MSC.Nastran计算，提交106非线性计算模块进行求解。
根据特征值法及106模块计算结果，屈曲首先会发生在梁腹板孔的45度方向，分别取上述位置处单元剪应变，绘制载荷-应变曲线见图7。由载荷-应变曲线可知，当载荷增加到13.953kN时，40号片Z1和Z2面剪应变曲线首先产生明显的分叉现象，此时试验件发生屈曲。
对比试验结果可知，弧长法屈曲载荷值与试验结果相差0.75%。
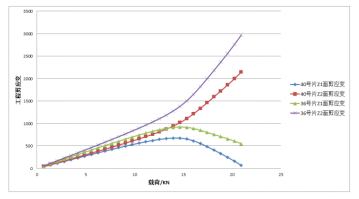
图7 载荷-应变曲线
3结论
通过对某型民机复合材料平尾盒段梁腹板剪切稳定性试验研究，使用不同的计算方法得到试验件屈曲载荷，结合试验数据对比分析，得到如下结论：
1.工程分析方法得到的屈曲载荷与试验结果仅相差0.68%，吻合度较高，同时计算方法快捷方便，但工程方法中无法考虑腹板上的开孔等细节对屈曲载荷的影响；
2.特征值分析法得到的屈曲载荷与试验结果相差22.56%，误差相对较大，但其对屈曲模态形式及屈曲部位判断仍然准确，并可将其结果应用于弧长法分析中；
3.有限元弧长法得到的屈曲载荷与试验结果仅相差0.75%，吻合度较高，且这种方法不受试验件形状、开孔等细节影响，具有较高的可信度与操作性；
4.通过试验数据结果可知，试验件屈曲载荷集中在13.81kN～15.07kN(132%～144%的试验载荷)，试验件屈曲后仍能承受载荷，直至载荷达到试验大纲规定的最大载荷20.93kN（200%试验载荷）后试验件仍未破坏，显示出了较为明显的后屈曲能力，为类似结构的优化设计提供了思路和数据参考。
参考文献：
[1]石经纬，赵娟，刘传军，等.复合材料一面壁板剪切稳定性[J].复合材料学报，2020,37（7）：1590-1600
[2]航空航天工业部科学技术研究院.复合材料结构设计手册[M].北京：航空工业出版社，1990.224-244，361-395
[3]许良梁.复合材料层合板前剪切屈曲及后屈曲行为研究.西北工业大学硕士学位论文，2006
[4]李珊山，魏玉龙，陈先民.机翼盒段梁腹板剪切稳定性试验与分析[J].第23届全国结构工程学术会议论文集，2014
[5]尹剑.复合材料受剪梁腹板稳定性试验及数值分析[J].科技创新导报，2014,309（21）
[6]唐劼尧，柏敏建.轴压载荷下复合材料蜂窝夹层板的稳定性研究[J].兵器设备工程学报，2020,41(09):242-246
