引 言
近年来,材料在高温高压下的结构与性质研究已经成为一个前沿的研究领域,特别是金刚石对顶砧(DAC)技术发明以来,在实验室中可以产生500~1000万大气压的静态压力,使得人们对材料在极端外界条件下的特性有了更先进的认识手段,也掀起了对硫族锌化物ZnX(X=O,S,Se,Te)材料研究的热潮。在高压环境下,ZnO和ZnS都是从闪锌矿(ZB)结构向岩盐(RS)结构转变,但ZB结构的ZnSe到底是向RS还是向朱砂相(CB)结构转变还存在很大的争议。而且,在结构相变过程中,出现了一些新的变化值得去研究,包括高压导致的原子配位数的增加、能带结构的变化和半导体-金属特性的转变等。
ZnTe材料在自然条件下有ZB结构和纤锌矿(WZ)结构,可以广泛应用于各种光电子器件中。到目前为止,研究者从实验和理论方面对ZnTe材料在高压下的结构已进行了一系列的研究。作为ZnTe材料中常见构型的六角WZ结构,锌原子占据层与氧原子占据层分别交错排列, 各自形成一个极性面,是具有自发极化的最高对称性的结构,本文将运用投影缀加波赝势方法,着力研究WZ结构的ZnTe在高压下的结构特性和相变问题,本研究有助于理解ZnTe材料在极端外界条件下的物理性质,突破高温高压实验条件限制的瓶颈,探索其在复杂环境下的应用潜力。
1 计算方法和模型
WZ结构ZnTe的空间群为P63mc,Zn原子在(0.3333,0.6667,0)处,Te原子在(0.3333,0.6667,0.375)处。为了系统地研究WZ结构的稳定性和结构相变情况,ZnTe材料的其它几种常见结构(ZB、CB和Cmcm)也作为参考对象。本文是基于密度泛函理论下的投影缀加波(PAW)方法,交换-关联能用广义梯度近似(GGA)方法来处理,离子实和价电子之间的相互作用用赝势(PP)来描述。计算时,根据空间群、晶格参数和原子坐标来确定晶格结构和原子位置。本文的结构优化是用VASP程序来完成,为确保计算速度和足够的精度,并满足结果收敛的要求,本文计算的平面波截止能量(Cutoff energy)取400 eV,Monkhorst-pack网格大小为8×8×8,原子间的相互作用力的收敛标准是0.01 eV/Å,能量的收敛标准是1 meV/atom。
在计算零压下的弹性常数时,采用非体积守恒张力的方法。弹性常数和有限张力变量的关系如下
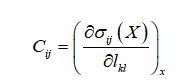 (1)
(1)
式(1)中,![]() 和
和![]()
![]() 分别表示施加的压力张量和欧拉应变张量;X和x分别表示形变前和形变后的坐标。
分别表示施加的压力张量和欧拉应变张量;X和x分别表示形变前和形变后的坐标。
2 状态方程及结构相变
首先分别选取ZnTe四种结构(WZ、ZB、CB和Cmcm)实验上测量出的晶格参数,在零压下对原胞进行几何优化,得到最稳定的结构。然后以此结构为基础,改变晶格参数的大小来计算总能量,作出总能量随体积变化的关系曲线。最后,用Brich-Murnghan (B-M)状态方程
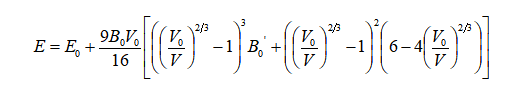 (2)
(2)
进行数据拟合,其中E0和V0分别代表零压下原胞的总能量和体积,为体模量,为体模量对压力的一阶导数。
图1为四种结构原胞的总能量随体积变化的关系曲线。零压下,优化后的WZ结构的晶格常数、弹性常数、体模量及体模量对压力的一阶导数和杨氏模量分别列于表1中。从表中可以看出,WZ结构的晶格参数a和c与其它结果符合得较好,c/a大小也非常接近理想六方晶胞比例。内部结构坐标u和实验结果大小是一致的,但是比理论值略大一些。表1中还给出了弹性常数的五个独立分量,根据弹性常数即可求解出六角晶系的体模量Bhcp的大小,结果为51.01 GPa。B和B'的拟合结果分别为44.93 GPa和4.60,与其它理论结果都符合得较好,将其代入方程(2)即可得到WZ结构的状态方程。ZnTe材料的杨氏模量在垂直c轴方向上的大小相同,但是远大于沿着c轴方向上的大小,证明WZ结构c轴方向比其它方向更容易发生形变,属于力学性能各向异性的晶体,这和六角结构的超硬材料RhB力学特性类似。
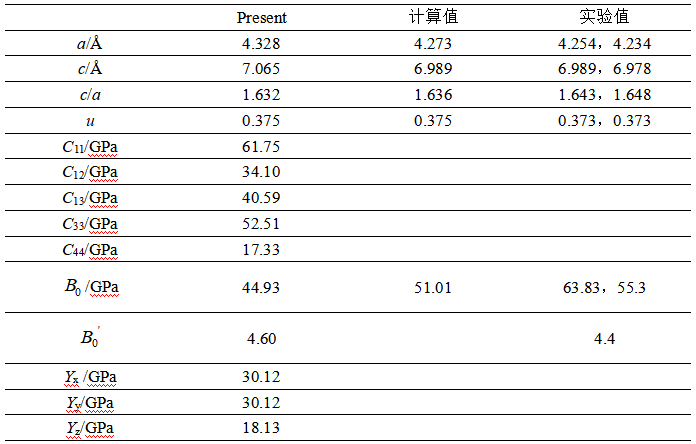
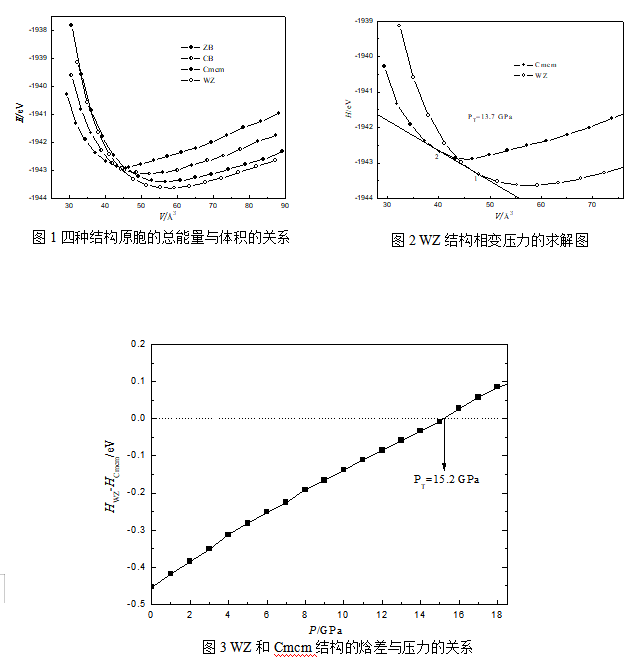
从图1中可以看出,在零压下,WZ结构和ZB结构的能量随体积的变化关系比较接近,但前者的最低能量比后者还要低0.2 eV左右,是所有构型中最稳定的结构。这一点和WZ结构的MnTe和ZnO类似,也是比其相应的ZB结构的能量低。从图可知,随着压力的增加,低压相的WZ和ZB结构都会向高压相结构转变而发生一级结构相变,但两者之间不会发生相变。由于WZ、CB和Cmcm三者结构曲线交点比较靠近,无法直观地判断出在高压下WZ是向CB结构,还是向Cmcm结构转变。
通常情况下,由室温引起的熵对Gibbs自由能()的贡献很小,可以忽略不计, 因此可以通过焓对体积的变化来研究相变压力和临界体积。因为总能量与体积的两条关系曲线存在一条公切线,这条公切线的斜率的负数就是相变压力。由图1可作出WZ和CB及CB和Cmcm曲线的两条公切线,得到的相变压力分别为16.4 GPa和10.8 GPa,结果证明中间的CB结构是亚稳相,最终还是会转变为Cmcm结构。所以,WZ结构应该是直接向Cmcm结构发生相变,如图2 所示,公切线和两条曲线的切点分别为1和2,由此求得的相变压力为13.7 GPa。为了进一步证实WZ结构的相变情况,还研究了焓()对压力的变化关系。如果两种结构的焓相等,相应的压力也相等,此时材料将发生结构相变。由图3可知,WZ结构向Cmcm结构转变的相变压力为15.2 GPa。以上两种方法计算的结果比从头计算分子动力学计算的相变压力16 GPa略小一些。从图2中切点1和2,还可以推导出WZ和Cmcm结构的相对临界体积(以最稳定的WZ结构原胞体积为标准),结果分别为0.799和0.672。这表明,当达到相变压力时,WZ晶胞的体积相对稳定结构缩小了20.1%,此时开始转变为Cmcm结构,相变后的体积压缩率为12.7%,路径1—2代表两者共存的混合相。
3 结 论
利用密度泛函理论下的投影缀加波方法,对WZ结构ZnTe材料的结构相变进行了研究。与其它几种常见结构比较,WZ结构和ZB结构的能量-体积曲线比较接近,同时表明WZ结构是最稳定的结构。当外界压力达到一定的大小时,WZ结构向Cmcm结构转变而发生结构相变,用两种方法计算出的临界相变压力分别为13.7 GPa和15.2 GPa。而且,计算出的零压下的晶格常数、弹性常数、体模量和杨氏模量大小均与其它理论值和实验值符合得很好。本结果为高温高压下ZnTe材料的性质探索和极端环境下的应用研究提供了一些理论依据和参考。
参考文献
[1] Blöch P E, Projector augmented-wave method[J]. Physical Review B, 1994, 50 (24): 17953
[2] Perdew J P, Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities[J]. Physical Review Letters, 1983, 51(20): 1884
[3] Kresse G, Joubert D, From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B, 1999, 59(3): 1758










