一、引言
习近平总书记在党的二十大报告中强调：“发展乡村特色产业，拓宽农民增收致富渠道”。农民画绘画产业作为农民增收的支柱性产业之一，近些年越来越受到学者的关注，在发展政策分析、发展不足分析、产业发展研究等进行了较多的研究。但少有从利益相关者角度出发，对其品牌建设进行研究和探讨各利益相关者间交互关系与协同决策，而运用演化博弈理论[1]来分析这一过程的研究则更加少见。因此，亟待对农民画品牌建设进行深度研究，探讨利益主体的协同策略。基于此，本文将在现有文献基础上，运用演化博弈理论，构建农民画生产组织、地方政府和经销商之间的三方演化博弈模型，探究影响农民画品牌建设的因素及利益相关者作用，并对各博弈主体行为及演化稳定策略进行讨论，为农民画品牌建设提供参考。
二、模型构建
（一）问题描述
在农民画品牌建设过程中，涉及到的主要利益主体包括农民画生产组织、地方政府以及经销商。三者策略相互影响且均为有限理性，各方策略处于动态变化中，为实现自身利益最大化，不断调整策略，最终三方策略趋于稳定，实现博弈均衡。三方演化博弈主体之间的逻辑关系如图1所示。
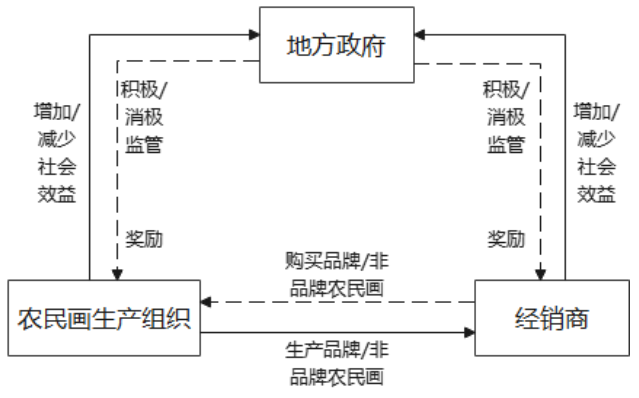图1三方演化博弈模型逻辑关系图
1.模型假设
假设1：三方主体均有两种策略可选择。农民画生产组织选择生产品牌农民画的概率为x（0≤x≤1），生产非品牌农民画的概率为（1−x）。地方政府选择积极监管的概率为y（0≤y≤1），消极监管的概率为（1−y）。经销商选择购买品牌农民画的概率为z（0≤z≤1），购买非品牌农民画的概率为（1−z）。
假设2：农民画生产组织选择生产品牌农民画时，需要在多方面投入更高的成本，设生产成本为CP。地方政府选择积极监管策略意味着要对品牌农民画生产行为和质量进行严格监管，设新增的监管成本为Cg；经销商选择购买品牌农民画会比购买非品牌农民画付出更高的成本，设增加的成本为Cb。
假设3：选择积极监管的地方政府会给予愿意参与品牌农民画建设的农民画生产组织和经销商一定的奖励，故设增加的奖励总额为R。其中，农民画生产组织增量奖励系数为λ，经销商增量奖励系数为1−λ。
假设4：农民画生产组织选择生产品牌农民画带来的增量经营收益取决于经销商多支付的成本，故设为αCb（0<α<1）。地方政府获得收益的情景有两类：一是若农民画生产组织选择生产品牌农民画，则区域公共农民画品牌的影响力增强，获得社会效益的增加量为Bg；二是采取积极监管策略的地方政府会获得中央政府的奖励为A，为确保激励有效，奖励A应至少覆盖地方政府积极监管应付出的监管成本和承担的公共投资成本最小值（A>Cg）。购买品牌农民画的经销商会获得的增量效用为Ba。
假设5：市场交易损益。当产品能较好地满足市场需求，双方达成交易且交易成本较低，双方各自获得的协同收益为Ι。相反，市场交易的协同收益丧失，农民画生产组织会面临产品滞销困境，地区经济发展会受到不利影响，故设地方政府的损失为Lg，农民画生产组织的损失为Lp。另外，农民画消费的普遍性决定就地、就市购买农民画是绝大多数经销商的选择，故假设0<Ba−Cb<Ι。
2.收益矩阵
基于上述模型假设,得到模型的收益矩阵，如表1所示。
表1收益矩阵表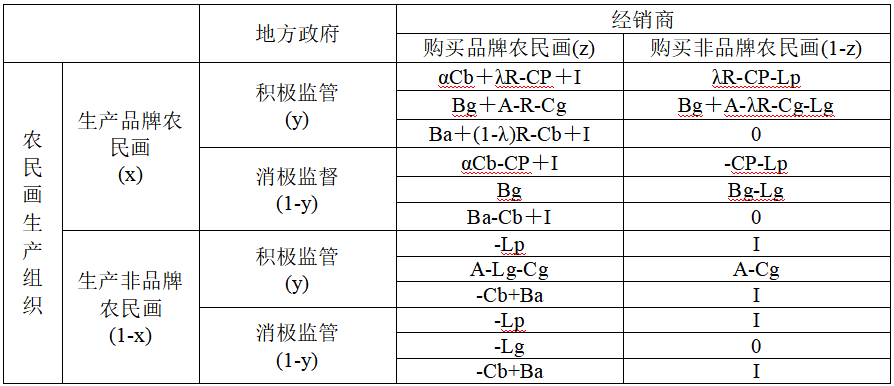
（二）模型分析
1. 演化稳定策略分析
（1）农民画生存组织策略选择的复制动态方程
生产品牌农民画的期望收益为E11，生产非品牌农民画的期望收益为E10，平均期望收益为E1。
E11=yz[(αCb＋λR-CP＋Ι)]+y(1-z)[λR-CP-Lp]+(1-y)z(αCb-CP＋Ι)+(1-y)(1-z)-CP-Lp
E10=yz(-Lp)+y(1-z)Ι+(1-y)z(-Lp)+(1-y)(1-z)Ι
E1=xE11+(1-x)E10
农民画生产组织策略选择的复制动态方程为：
F(x)=dx/dt=x(E11-E1)=x(1-x)[-(CP+Lp+Ι)+yλR+z(αCb+2Ι+2Lp)]
（2）地方政府策略选择的复制动态方程
地方政府选择积极监管的期望收益为E21，消极监管的期望收益为E20，平均期望收益为E2。
E21=xz(Bg+A-R-Cg)+x(1-z)[Bg+A-λR-Cg-Lg]+(1-x)z(A-Lg-Cg)+(1-x)(1-z)(A-Cg)
E20=xzBg+x(1-z)(Bg-Lg)+(1-x)z(-Lg)
E2=yE21+(1-y)E20
地方政府策略选择的复制动态方程为：
F(y)=dy/dt=y(E21-E2)=y(1-y)[A-Cg-λRx+xz(λR-R)]
（3）经销商策略选择的复制动态方程
设经销商选择购买品牌农民画的期望收益为E31，购买非品牌农民画的期望收益为E30，平均期望收益为E3。
E31=xy[(1-λ)R-Cb+Ba+Ι]+x(1-y)[-Cb+Ba+Ι]+(1-x)y(-Cb+Ba)+(1-x)(1-y)(-Cb+Ba)
E30=(1-x)yΙ+(1-x)(1-y)Ι
E3=zE31+(1-z)E30
经销商策略选择的复制动态方程为：
F(z)=dz/dt=z(E31-E3)=z(1-z)[-Cb+Ba-Ι+(1-λ)Ryx+2Ιx]
2.演化博弈均衡分析
三方主体策略稳定性方程：
在单个主体策略稳定性分析的基础上，进一步对三方主体演化博弈系统均衡点的稳定性进行分析，由F(x)=0，F(y)=0，F(z)=0可得系统均衡点。由于非对称博弈要求演化稳定策略一定是严格纳什均衡，故本文只需讨论E1(0,0,0)、E2(1,0,0)、E3(0,1,0)、E4(0,0,1)、E5(1,1,0)、E6(1,0,1)、E7(0,1,1)、E8(1,1,1)8个纯策略均衡点的稳定性。通过计算三方主体演化博弈系统的Jacobian矩阵可得：
其中：
a11=（1-2x）[-(Cp+Lp+I)+βλR+z(αCb+2I+2Lp)]，
a12=x(1-x)λR， a13=x(1-x)(λCb+2I+2Lp)，
a21=β(1-β)[-λR+z(λR-R)]， a22=(1-2β)[A-Cg-λRx+xz(λR-R)]，
a23=β(1-β)[(λR-R)x]， a31=z(1-z)[(1-λ)Rβ+2I]，
a32=z(1-z)(1-λ)Rx， a33=(1-2z)[-Cb+Ba-I+1-λRβx+2Ix].
为了分析均衡点的稳定性，使用Routh-Hurwitz判据，若3个特征值均为负数,则为演化稳定策略；若3个特征值存在有正数,则为不稳定点。计算矩阵（14）在各平衡点的特征值可得复制动态系统的演化稳定策略，如表2所示。
表2复制动态系统的演化稳定策略
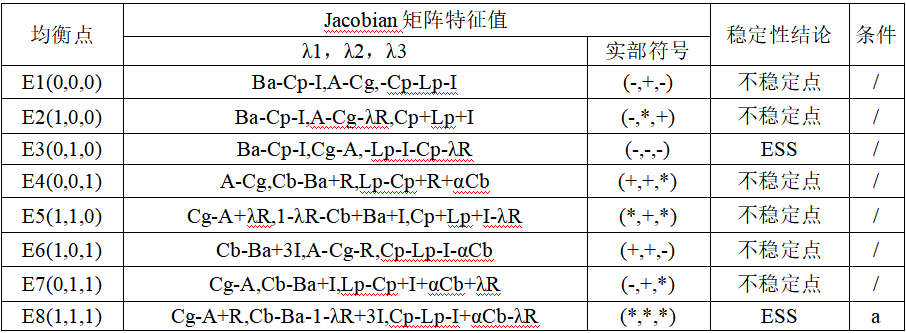*代表不能确定特征值实部的正负号，a表示可使模型在平衡点E8(1,1,1)稳定的条件。我们可以找到一个使模型（13）在E8（1,1,1）点渐近稳定的充分条件，三方愿意共同参与建设品牌农民画。
A-Cg-R>0，(Ba-Cb-Cp+2I+Lp+R+Cbα)>0，Ba-Cb+I+R-RλCp-I-Lp-Cbα-Rλ<0.
此外，可求得模型（13）在E8（1,1,1）处的特征方程为：
(A-Cg-R+x)(x2+x(Ba-Cb-Cp+2I+Lp+R+Cbα)-(Ba-Cb+I+R-Rλ)(Cp-I-Lp-Cbα-Rλ))=0.
显然方程（16）有一根x1=Cg-A+R。进一步由一元二次方程根与系数的关系可知，当条件（15）成立时，方程（16）的全部特征值为负，所以模型在E8（1,1,1）点渐近稳定。
（三）结论与建议
基于乡村振兴视角下农民画品牌建设的实践背景，构建三方演化博弈模型，系统地分析三方主体策略选择和博弈系统均衡点。结果表明，三方演化博弈系统存在<生产品牌农民画，积极监管，购买品牌农民画>和<生产非品牌农民画，消极监管，购买非品牌农民画>两个演化稳定策略组合，并给出以下建议: 第一，中央政府应加大对采取积极监管策略地方政府的奖励额度，减轻地方政府参与农民画品牌建设的财政压力，地方政府在参与农民画品牌建设中应发挥正确引导作用。第二，农民画生产组织应科学运营，打造可替代性低、附加值高的农民画品牌，以充分发挥品牌农民画供给对消费升级的支撑与引领作用。第三，经销商应紧跟农民画品牌市场化导向，兼顾社会责任与经济利益，进行精细化品牌推广，以培养和巩固消费者购买品牌农民画的消费惯性。
