1研究背景
当今世界已进入数字化时代,我国也相继提出“两化深度融合”和“中国制造2025”等战略,鼓励制造业开展数字化转型,推动数字技术与实体经济深度融合[1]。第四次全国经济普查数据显示[2],我国中小型企业具有“五六七八九”的典型特征(贡献50%以上税收、60%以上GDP、70%以上技术创新、80%以上城镇劳动就业、90%以上企业数量),是制造业数字化转型的主战场、数字经济发展的主力军[3],但目前存在紧迫性不强、需求不明确、数字化基础薄弱等问题[4]。
智能制造是中小型制造业实现数字化转型升级的必然趋势[5],由于每个行业、每家企业、每项业务的情况千差万别,需要分别对各个企业的智能制造难点、痛点进行诊断分析和差距分析,找出短板或薄弱环节,并量身定制个性化、系统性的智能制造解决方案,才能精准高效地完成数字化升级改造[6][7]。当前主要通过基于权重法的智能制造诊断模型为企业进行咨询诊断[8],即列举一系列问题让企业进行回答,每个选项对应不同得分,将所有问题的得分乘以相应的权重,便得到该企业在智能制造方面的总体得分,从而获得该企业在数字化转型领域的定位与评级,再针对性地提出数字化转型建议方案。
然而,由于各细分行业差异较大,企业之间也有所差别,该方法并不能体现出单个企业在智能制造方面的指标与需求[9]。此外,现阶段的诊断模型侧重于问题设置+企业定位与诊断两方面的内容,在后续的环节(即选择解决方案与产品组合,以及效果分析与指标评估)涉足甚少,即使研判出企业当前的定位与问题,也无法明确提供相对应的解决方案及其实施效果。综上所述,现阶段基于权重法的智能制造诊断模型无法为企业提供针对性较强的诊断结果和解决方案,考虑到决策树分析法多次被用于各类故障诊断模型[10][11][12],本研究尝试将该法用于企业智能制造诊断模型。
2研究内容
本研究采用决策树分析的方法为企业提供智能制造诊断模型,即企业通过选择不同的选项,应答相匹配的问题,进而引导出不同的答题路径,得到针对企业自身的定位与诊断。并且以此出发,提供适当的解决方案组合,评估应用某项技术或解决方案后的实施效果。
具体实施步骤如图1所示:
(1)问题应答阶段。利用决策树分析的方法,从根节点(一般为智能制造二级分类,以研发分类为例)出发,在节点处有第一个问题,通过第一个问题的几个选项进行选择(如A1或A2,每个问题的分值不同,智能制造三级指标),根据选择结果再在下级节点处进行选择(选择A1的企业针对B1或B2进行选择,选择A2的企业针对B3或B4进行选择…),选择A1后的问题和选择A2后的问题不同,依此类推,最后依托此决策树分析办法,企业会根据自身的实际情况形成一条专属的答题路径。在此路径中各个三级指标都彼此关联,有很强的相关性与延续性。因此企业回答的都是最贴合其智能制造发展情况的问题,针对性较强,更能引导出企业当前的真实状态与定位。
(2)企业得分与定位。通过各节点的选择,到达状态节点N1,即企业智能制造各分类(即二级指标)的得分与定位。一般情况下不同企业的路径会对应不同的状态节点N1,即不同的得分。不过也有一些情况下两家企业由不同的路径引导,可能会得到相同的状态节点N1,即相同的得分。但因为路径的不同,模型后续提供的解决方案也会有所区别。企业智能制造的整体得分(即一级指标)可以通过各二级指标的加权平均值或平均值乘以系数的方式得到。
(3)解决方案组合。由N1引出S1、S2、S3…等解决方案分枝,进行解决方案的选择。提供的S1、S2、S3等潜在解决方案与答题路径的各三级指标以及二级指标N1强相关,因此具有足够明确的针对性与匹配性。
(4)应用效果评估。选择某项解决方案(或组合,假设为S2),生成企业应用后产生的提质、降本、增效等方面的效果,即E1。企业可以对比应用某项解决方案(或组合)的前后差异,并作为最终是否上马与实施该解决方案的参考依据之一。
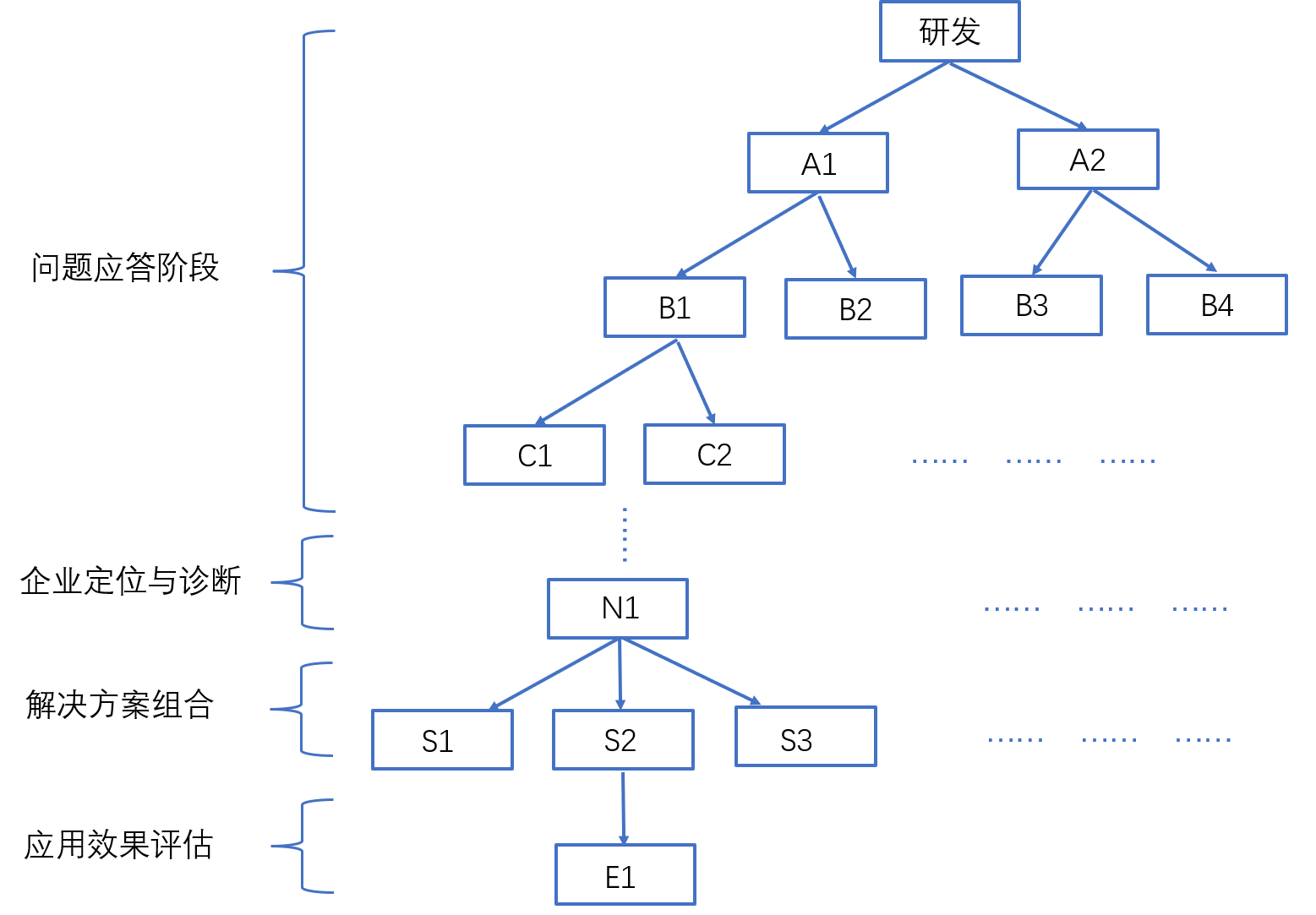
图1 基于决策树分析的智能制造诊断模型流程
例如在研发分类中,第一个问题可以是企业是否在智能制造的研发层面有投入,选项A1为有投入,A2为没有投入。如果选择A1,会有第二个问题为企业在智能制造研发的投入占企业利润的百分比是多少,选项B1为大于10%,选项B2为小于10%;如果选择A2,会有第二个问题为企业是否在一年内计划在智能制造研发上有投入,选项B3为有,选项B4为没有。以此类推,当回答到第N个问题时,企业选择N1选项,此时会有结果判断企业在智能制造研发上的情况是什么,相应的会有个评分和结论。根据此评分和结论可以提供出相应的解决方案S1、S2、S3…,选择某项解决方案后会提供给企业方案介绍和根据选定的方案S2实施后预计达到的效果E1。
基于决策树分析的诊断模型分数的计算依据是根据问题的不同选项得到的分数不同,从第一个问题开始,分数就开始计算,根据第一个问题的选项,选A1后续得分会在20-100分之间,选A2后续得分会在0-20分之间。然后到了第二题,如果选择B1分数会在60-100分,选B2分数会在20-60分。依次类推,每个题目的选分区间,也会出现不同的问题,最后的分数会有差异,这会体现在该类别最终的评分和结论中(即二级指标得分)。当一个分类的总分计算出来后,将所有的分类(比如研发、制造、安全等)的分数加权平均,计算出智能制造的总分(即一级指标),给出整体解决方案。从现状评估到解决方案再到预期效果,此模型可以给用户提供一整套智能解决方案,便于企业高效的分析企业智能制造的水平和为后续提升智能制造水平提出改进措施。
企业智能制造的整体得分(即一级指标)可以通过各二级指标的加权平均值或平均值乘以系数的方式得到。二级指标的加权值或系数根据信息量和企业的指标值等定义可用的若干个变量,采用线性回归、逻辑回归或KNN算法模型,设置模型取舍点阈值,利用模型K-S检验值和企业特征曲线对模型精确性和稳定性进行评估,评估后对模型进行调整,调整直到模型K-S检验值和企业特征曲线达到预期加权值或系数,随着评估企业的数量增加,进行模型调优,不断优化算法结果,得出企业的评估诊断结果的分级分类。运用数据挖掘和机器学习算法将企业属性画像作为特征指标构建企业评分模型,将评估分数划分为一、二、三、四,四个等级,根据企业评分结果,输出企业评估报告。
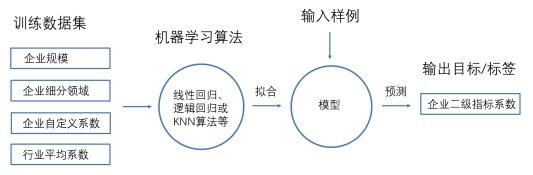
图2 企业二级指标系数计算方法
通过机器学习自动调整企业二级指标加权值或系数的方法如图3所示。首先获取若干组训练数据集(包含企业规模、企业细分领域、企业自定义系数、行业平均系数等变量),利用这些数据集,结合线性回归、逻辑回归或KNN算法等机器学习回归算法,可以拟合出二级指标系数模型。以线性回归为例,构建方程:
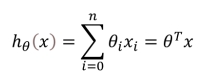
其中x是训练样本的特征值(例如企业规模、企业自定义系数、行业平均系数等),目的就是通过找出最合适的权重值θ,使得对于每个样本方程中 ε(误差)值最小。其中y就是训练目标,即企业二级指标系数。
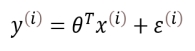
同时通过新产生的训练数据,不断优化并调整模型,利用模型K-S检验值和企业特征曲线对模型进行评估,使其能够最大程度反映某行业细分领域内的企业在一定规模下的二级指标系数。最后输入样例(即特定的企业),即可预测并输出该企业的二级指标系数。
3研究结论
相比于基于权重法的诊断模型,本研究具有以下优点:
1、能够更加准确地定位企业智能制造发展的阶段与现状。通过决策树分析法,企业能够应答更具有针对性的、适合企业自身的题目,选择最贴合企业当前发展状态的选项,进而引导出企业独有的答题路径,衍生出针对当前企业的指标定位与解决方案。因为同一行业内各个企业的数字化发展水平亦是千差万别,通过每家企业在使用该诊断模型时应答不同的问题与选项,能够最大程度地做到“具体企业,具体分析”,从而实现企业智能制造发展阶段与现状的精准定位与研判。
2、能够针对性地提供相匹配的解决方案(或组合),及评估应用某套解决方案之后产生的效果。通过决策树的方法,能分析企业的答题情况,结合企业评估结果,在后续的问题中及时提供相应的解决方案供企业选择,并根据选择的解决方案(或组合)结果获得大概的预测效果。这样可以直观、量化地展示解决方案应用到具体企业或项目上的作用与价值,引导企业找到解决自身数字化转型最适合的方案与路径。
3、采取机器学习的方式,能够自动调整模型里应用的系数。诊断的企业越多,通过人工智能训练获得的系数会优化得越精确。同时省去了人工调参的繁琐与误差。
综上所述,本研究通过决策树分析法构建一套科学、全面的智能制造诊断模型帮助中小型制造业评估自己智能制造所处的水平,找到智能制造实施的重点,指明智能制造的发展目标和发展方向,并可为当前急需解决的智能制造任务进行排序和设置优先级,助力企业精准高效地开展数字化转型,推动我国制造业全面转型升级。此外,还可通过每年定期进行智能制造诊断,引导和促进企业智能制造能力水平持续提升。
4参考文献
[1] 王一凡, 赵显立. “智能制造”:推进两化深度融合的战略选择[J]. 国防科技工业, 2015(10):2.
[2] 朱铎先, 毕延洁. 中小制造企业数字化转型之道[J]. 中国信息化, 2021(9):4.
[3] 任晞, 许峰. 制造业中小企业数字化转型研究——基于台州市L区424份调查问卷的分析[J]. 辽宁行政学院学报, 2021(1):6.
[4] 曹智铭. 论数字经济下中小企业高质量发展转型[J]. 中国总会计师, 2021(12):3.
[5] 王金涛, 李晓婷. 数字化转型:中小企业“跃龙门”的最后一跳[J]. 发明与创新:大科技, 2021(10):2.
[6] 柏隽. 制造业中小企业数字化转型“五步走”[J]. 中国工业评论, 2018.
[7] 朱宏任. 以高质量咨询服务助推企业数字化发展[J]. 企业管理, 2018(12):3.
[8] 赖冬,刘波涛, 胡洋,等. 基于成熟度模型的智能制造能力评估诊断[J]. 中小企业管理与科技, 2020(22):2.
[9] 李春花. 基于工业企业的智能制造需求分析[J]. 铜业工程, 2019(1):4.
[10] 刘继清, 黄金花. 基于改进决策树算法的设备故障智能诊断模型[J]. 制造业自动化, 2011, 33(7):4.
[11] 赵智聪, 肖乾柯, 刘治红. 基于C4.5决策树的装药车间设备故障诊断系统[J]. 机电产品开发与创新, 2021, 35(2):3.
[12] 王惠莲. 决策树算法在火电机组故障诊断中的应用[D]. 华北电力大学(北京), 2006.










