0 前言
工业机器人广泛应用于搬运、焊接、加工、装配等领域，随着市场的持续增长，对机器人性能提出了更高要求。作为一个复杂的动力学系统，机器人的动力学问题不容忽视，而动力学模型的准确性直接影响机器人动力学性能和控制精度。
针对机器人的动力学问题，国内外学者开展了许多方面的研究。理论方面，基于牛顿-欧拉法、拉格朗日法、Huston-Kane方法等建立机器人动力学模型[1-3]，并在动力学方程中添加摩擦项[4-7]，来提高动力学模型的准确性。但是转动惯量方面只考虑了绕关节轴旋转的机械臂结构等，而机器人关节传动系统复杂，内部的旋转部件未能考虑，其会对动力学模型准确性产生影响。
随着仿真技术的发展，很多学者应用Adams、Matlab/SimMechanics等动力学软件开展了机器人动力学分析[8-10]。但同样存在未能考虑传动系统内部旋转部件的惯量影响，而且对减速机的影响未做任何处理，仿真模型准确性差。
本文针对六关节工业机器人，充分考虑关节传动系统内部旋转部件惯量和减速机的影响，应用多体动力学软件ADAMS建立六关节工业机器人刚体动力学仿真模型，仿真计算得到各关节的扭矩，并通过试验测试验证了仿真方法的准确性。
1 几何模型建立
本文应用三维软件建立工业机器人的三维实体模型，忽略螺钉、密封圈、编码器线、动力线、护线板等质量较轻，对整机仿真计算影响不大的零件。简化后的六关节工业机器人结构示意图如图1所示，主要由基座、第一关节臂至第五关节臂、末端法兰盘、第一电机至第六电机、第一减速机至第六减速机、各关节臂侧板等组成。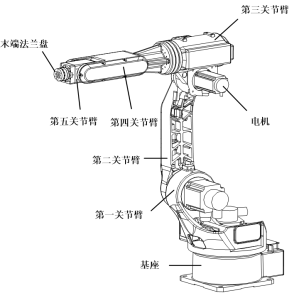
图1 六关节工业机器人结构示意图
2 刚体动力学仿真模型建立
ADAMS是集建模、求解、可视化技术于一体的虚拟样机软件，其采用拉格朗日方程方法建立系统的动力学方程，在机器人动力学仿真中有着广泛的应用。
本文采用ADAMS建立六关节工业机器人的刚体动力学模型。
将建立的机器人三维模型通过中间格式导入到ADAMS软件中，按照各部分的实际材料赋予材料属性，并根据装配关系和运动形式添加约束和连接，主要包括固定副和旋转副，初步搭建六关节机器人刚体动力学模型。
为了提高机器人动力学仿真模型的准确性，需要对机器人传动系统进行细致化处理，同时考虑减速机效率的影响。
2.1 关节传动系统建立
机器人关节传动系统一般由电机、减速机、同步带轮、齿轮等共同组成或者部分组成，各部分旋转共同驱动机器人关节运动，它们自身的转动惯量同样会对机器人的动力学性能产生影响，所以需要将各部分的惯量引入到动力学模型中。
以机器人第四关节为例，对其传动系统进行细致化处理，如图2所示：
（1）电机模型分解为电机外壳和电机转子，电机转子旋转体现电机惯量；
（2）建立同步带轮模型，旋转体现各自惯量。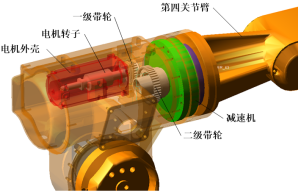
图2 第四关节传动系统示意图
（3）传动路径为：电机转子带动一级带轮旋转，与二级带轮旋转耦合形成减速比，二级带轮带动减速机旋转，与第四关节臂旋转耦合形成减速比，如图3所示。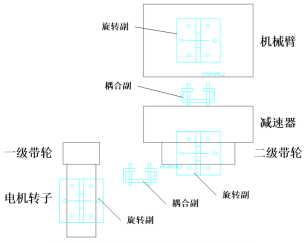
图3 第四关节传动系统传动路径示意图
机器人其他关节传动系统可以按照类似方式进行处理。
2.2 减速机效率等效处理
减速机作为机器人关节最主要的部件，其结构复杂，动力传递过程中存在消耗损失（即减速机效率），会对机器人动力学的准确性产生较大影响。
减速机效率损失主要是其内部结构旋转损失和接触摩擦损失，为简化仿真模型，将减速机模型简化为实体结构，采用旋转副摩擦扭矩来等效减速机效率。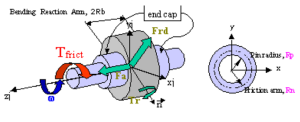
图4 旋转副模型结构示意图
ADAMS中旋转副模型的结构如图4所示。其摩擦扭矩由关节轴向支反力（Fa）、径向支反力（Fr）、弯矩（Tr）和初始扭矩（
）决定，其计算公式如下：
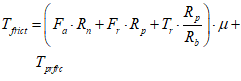(1)式中，Rn为摩擦圆半径，Rp为轴颈半径，Rb为弯曲作用力臂，
为摩擦系数。
通过以上处理，得到六关节工业机器人高精度的刚体动力学仿真模型，开展动力学仿真计算即可得到机器人每个关节的扭矩及末端运行状态。
3 试验测试
为验证六关节工业机器人刚体动力学仿真模型的准确性，建立机器人关节扭矩测试实验。
通过示波器采集机器人控制器中伺服电机驱动器的电源线UVW其中一相电流数据，然后通过计算处理得到电机的转速、扭矩和功率等结果，测试处理流程如图6所示。
为方便验证，测试工况采用额定负载100%速率下单轴运转，即一个关节在最大运动范围来回转动，而其他关节静止不动，测试得到各关节的扭矩结果。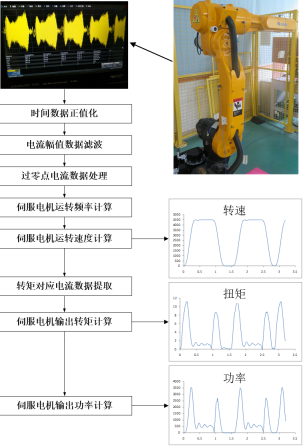
图6 机器人关节扭矩测试处理流程
4 结果分析
采用同样的工况，以各关节电机速度为驱动，开展机器人动力学仿真计算，得到各关节电机的扭矩结果，并与实验结果对比，为保证数据对比的一致性，将扭矩结果正值化。
由图7可以看出，单轴运转情况下，各关节电机扭矩基本呈逐步减小变化，与各轴的转动惯量相关；其中第一关节电机扭矩稍小于第二关节电机，主要由于第二关节转速较高，角加速度相对较大。
前半个周期和后半个周期分别对应机械臂的来回运转过程，扭矩结果基本一致，但第三关节和第五关节却出现不一致情况，主要由于重力作用影响，在前半个周期，重力作用与关节运转方向一致，而在后半个周期，重力作用与关节运转方向相反。
半个周期内，扭矩峰值有大小之分，其正好对应关节的加速和减速阶段，加速阶段峰值更大，减速阶段峰值较小，主要由于摩擦影响，加速阶段摩擦作用与驱动扭矩方向相反，而减速阶段摩擦作用与驱动扭矩方向一致，第三关节前半个周期加速阶段扭矩峰值小于减速阶段，主要受重力作用影响。
扭矩水平段对应关节匀速阶段，此阶段扭矩主要是摩擦作用引起，通过对比可以发现，后面关节的摩擦扭矩损失占比越来越大。第二关节匀速阶段未出现扭矩水平段，是由于关节转动过程中，姿态改变致使重力作用产生的力矩随之改变而引起。第三关节则没有对应的匀速阶段。
对比实验与仿真结果，两者结果保持高度吻合，峰值误差<8%，验证了六关节机器人刚体动力学仿真模型的准确性。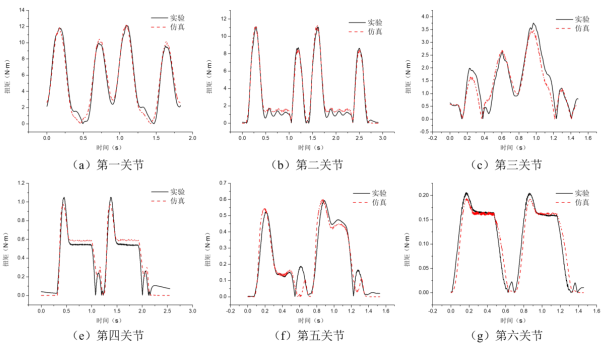
图7 各关节电机扭矩结果
在同样的工况下，将关节摩擦忽略，开展机器人动力学仿真，得到各关节电机的扭矩结果。
由图8可以看出，忽略关节摩擦后，加速阶段的扭矩和减速阶段的扭矩一致，第三关节除外，其主要受重力影响。在匀速阶段，关节扭矩基本为零，此时加速度为零，第二关节和第五关节扭矩不为零，同样因为受到重力影响。
用实验测试结果减去忽略摩擦的仿真结果即可得到机器人关节扭矩损失结果，即减速机的扭矩损失。
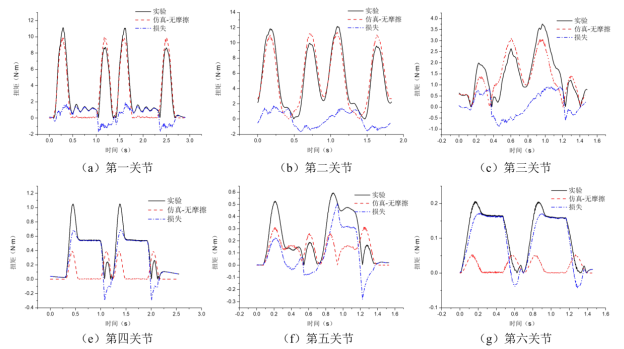图8 各关节电机扭矩结果（无摩擦）
在加速阶段，关节损失逐步增加，到水平阶段有所回落，而在减速阶段，关节损失为负值，即表明此时摩擦变成了有用功。前三个关节的扭矩损失占比相对较小，而后三个关节的扭矩损失占比相对较大，前三个关节采用RV减速机，而后三个关节采用谐波减速机，而RV减速机效率优于谐波减速机，与结果一致。
观察加速阶段的关节扭矩损失占比，可以发现前三个关节损失占比随转速增大而逐渐增大，即减速机效率降低，根据减速机样本数据可知，RV减速机效率随转速增大而减小，随扭矩增大而增大，与计算结果保持一致。后三个关节损失占比随转速增大先减小再增大，即减速机效率先升高再降低，与扭矩的变化规律一致，表明在较高扭矩时减速机效率更高。
5 结论
本文采用ADAMS建立了六关节工业机器人刚体动力学仿真方法，同时建立关节电机扭矩测试验证，进一步分析了关节扭矩损失情况，得到以下结论：
(1) 六关节工业机器人刚体动力学仿真关节电机扭矩与实验结果高度吻合，误差＜8%，表明了刚体动力学仿真方法的有效性。
(2) 关节电机扭矩受到加速度、惯量、重力、摩擦等多方面的影响，惯量和加速度对扭矩起决定性作用，关节越靠后关节扭矩越小。摩擦致使加速阶段扭矩峰值大于减速阶段，并在匀速阶段起主要作用。而重力仅对第二、第三和第五关节扭矩影响较大。
(3) 关节扭矩损失主要由减速机效率引起，可以由关节摩擦有效等效。前三个关节采用RV减速机，其效率较高，而后三个关节采用谐波减速机，其效率相对较低。加速阶段，前三个关节减速机效率随转速增大而降低，后三个关节减速机效率随扭矩的增大而升高，受转速影响较小。
六关节工业机器人刚体动力学仿真方法可以有效应用到机器人动力学性能评估分析中。本文初步分析了六关节工业机器人单轴运动的动力学性能，后续将进一步分析多轴联动的动力学性能。
参 考 文 献
[1] 卢锐. 工业用六轴机械臂的建模与仿真[D]. 中北大学, 2015.
LU Rui. Modeling and simulation of six-dof industrial manipulators[D]. North University of China. 2015.
[2] Toz M, Kucuk S. Dynamics simulation toolbox for industrial robot manipulators[J]. Computer Applications in Engineering Education, 2009, 18(2)：319-330.
[3] 王殿君, 关似玉, 陈亚, 等. 六自由度搬运机器人动力学分析及仿真[J]. 机械设计与制造, 2017(1)：25-29.
WANG Dianjun, GUAN Siyu, CHEN Ya, et al. Dynamic analysis and simulation of the carrying six-dof robot[J]. Machinery Design & Manufacture, 2017(1)：25-29.
[4] 毕德学, 孙国强, 许增朴. 机器人动力学模型识别新方法[J]. 天津科技大学学报, 2007, 22(1)：37-40.
BI Dexue, SUN Guoqiang, XU Zengpu. A new method for robot dynamics identification[J]. Journal of Tianjin University of Science & Technology, 2007, 22(1)：37-40.
[5] 王靖森, 刘晓峰, 段柳成, 等. 考虑关节摩擦的空间机器人动力学建模与参数辨识[J]. 力学季刊, 2015, 26(4)：594-601.
WANG Jingsen, LIU Xiaofeng, DUAN Liucheng, et al. Dynamic modeling and parameter identification of a space robot considering joint friction[J]. CHINESE QUARTERLY OF MECHANICS, 2015, 26(4)：594-601.
[6] 席万强, 陈柏, 丁力, 等. 考虑非线性摩擦模型的机器人动力学参数辨识[J]. 农业机械学报, 2017, 48(2)：393-399.
XI Wanqiang, CHEN Bai, DENG Li, et al. Dynamic parameter identification for robot manipulators with nonlinear friction model[J]. Transactions of The Chinese Society of Agricultural Machinery, 2017, 48(2)：393-399.
[7] Chernous'ko F L, Shunderyuk MM. The influence of friction forces on the dynamics of a two-link mobile robot[J]. Applied Mathematics and Mechanics, 2010, 74(1)：13-23.
[8] 孙奎, 谢宗武, 刘宏. 一种新的机器人动力学仿真分析方法[J]. 机械设计与制造, 2008(5)：163-165.
SUN Kui, XIE Zongwu, LIU Hong. The dynamics simulation analysis of a four DOF manipulator[J]. Machinery Design & Manufacture, 2008(5)：163-165.
[9] 李雨健. 六轴码垛机器人的轨迹规划与关节摩擦补偿研究[D]. 哈尔滨工业大学, 2016.
LI Yujian. Trajectory planning and research on friction compensation of six-axis palletizing robot[D]. Harbin Institute of Technology, 2016.
[10] 朱华炳, 张娟, 宋孝炳. 基于ADAMS的工业机器人运动学分析和仿真[J]. 机械设计与制造, 2013(5)：204-206.
ZHU Huabing, ZHANG Juan, SONG Xiaobing. Kinematic Analysis and Simulation of Industrial Robot Based on ADAMS[J]. Machinery Design & Manufacture, 2013(5)：204-206.
作者简介：孔令超(通信作者)，男，1985年出生，硕士研究生。主要研究方向为工业机器人。
