1引 言
在测量场空间基准网络的构建过程中,由于环境温度变化、振动及地基沉降等非稳态环境的因素存在,必然会导致基准点位置发生偏移,造成测量场构建精度损失。各种环境因素影响中,温度变化所引起的热漂移最为明显。目前绝大多数研发者采用热变形理论或有限元仿真技术预测计算出大型钢架钢架结构热变形。国外有些学者计算出飞机装配现场的适宜温度范围,然后采用一系列温度控制措施来保持装配现场的恒温条件,借此减小基准点热漂移,但恒温技术成本昂贵,不适合大部分飞机装配现场使用;本文所研究工装结构复杂,无法使用理论公式进行计算;工装处于装配车间(非露天),无法通过太阳这个热源来计算模拟工装非均匀温度场。因此,需要建立相关模型得到基准点热漂移的数值大小与方向,从而在飞机装配环节中提高测量场的构建精度。本文聚焦于基准点热漂移所引起的测量场精度损失,针对某大型工装建立基准点热漂移测量试验,选择特定时期积累测量试验场基准点温度和坐标漂移数据;基于前述数据采用BP神经网络算法构建非均匀温度场下大型工装热漂移代理模型;针对前述代理模型存在的迭代次数、精度、耗时等各方面问题引入粒子群优化算法对其初始权值和阈值进行优化,从而建立热漂移优化代理模型,并借此制定提升方案,达到提高测量场精度的研究目的。
2 神经网络模型
虽然测量试验在选定月份测量得到的数据可认为是环境温度变化引起的,但在非选定月份中情况并不如此即无法在工程实际中广泛应用,为此引入人工神经网络解决这一问题。在进行BP神经网络训练之前,先将测量得到的24组数据即1440个基准点所对应的热漂移数值大小及方向依据式1对其进行归一化处理:
(1)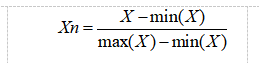
式中:Xn为归一化后的结果;X为学习数据样本。
2.1 BP神经网络算法
本文选择三层BP神经网络结构,所选用的传递函数为Sigmoid函数。BP神经网络在训练时为确保训练结果能够收敛,通常会将学习率设置的较小但这样却难以兼顾训练速度。此外,由于权值和阈值的初始随机性可能导致BP算法难以达到全局最优解。
2.2 粒子群算法
粒子群智能算法作为一种启发式优化算法,灵感来源于自然界中的群体行为,尤其是鸟群和鱼群的协同行为;前述行为的特点在于群体内的个体会相互传递信息从而有效达成集体目标。PSO算法与其类似,是通过模拟个体之间的协作与信息共享来寻找到问题的最优解,也正因如此PSO算法在全局优化问题和可行解空间较大时表现出色,在工程优化、机器学习、图像处理、智能控制等各个领域被采纳并得到了广泛的应用。
本文首先在可行解空间中随机生成一组粒子,每个粒子均代表在可行解空间的一个潜在解,用位置、速度和适应度值三项指标表示该粒子特征。粒子在可行解空间中进行运动,在每次迭代中粒子都会根据当前的位置、速度与适应值等更新自身状态,个体极值Pbest和群体极值gbest也会随着迭代的进行而实时更新,这种搜索更新机制使得粒子逐渐朝着全局最优解的方向收敛。
将神经网络中的权值和阀值映射为PSO中的粒子从而实现对参数的优化,步骤如下:
1) 对样本数据(输入:基准点名称代号、对应温度;训练目标:XYZ方向的热漂移数值)进行预处理。
2) 确定BP神经网络的相关参数。
3) 根据式2确定粒子群算法的粒子群维度:
(2)![]()
式中:ni、nh和no分别代表输入层、隐含层及输出层的神经元个数
确定每个粒子的适应度值,适应度的计算公式如式3所示:
(3)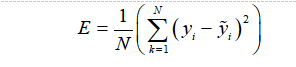
式中:N为输入基准点总数;yi为测量试验提取的基准点各个方向的热变形数值,i为神经网络预测的基准点各个方向的热漂移数值。
4) 确定粒子群算法的惯性权重w,本文采用线性递减惯性权重策略,如式4所示:
(4)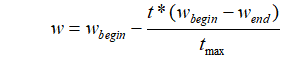
式中:wbegin、wend为惯性权重w初始时刻与最后一次迭代的惯性权重,经典取值分别为0.9与0.4,t表示当前迭代代数,tmax表示迭代次数的最大值。粒子群规模设为40,最大迭代次数设为1000,最大限制速度设为vmax=1,训练精度为0.0001,学习因子c1和c2都设为2.05。
5) 判断是否满足终止条件:一是预设精度,一是最大迭代次数,如果满足条件输出最优权值和阈值,不满足的话就返回步骤3)继续搜索。
6) 将优化后的权值和阈值作为神经网络的初始权值和阈值进行神经网络训练,得出神经网络训练结果。
3 预测效果对比
随机选取样本数据中的24组数据中的20组作为训练集,其余数据作为测试集。为了评估网络的准确性,采用均方根误差、平均绝对误差、平均相对误差来评价,这三种误差均可良好地评价出神经网络的性能。将1440个基准点的数据随机分为训练集与测试集,训练集与测试集分别具有1200个与240个基准点数据,图1为对测试集的网络精度进行对比结果。误差计算表明,采用BP神经网络得到的预测值的平均相对误差和决定系数在三个方向的平均值分别是0.1736和0.9868,而PSO-BP对应的数值则是0.1119和0.9903,由此得出以下结论:经过本文神经网络优化的结果相对于BP神经网络在精度上有了显著的提升,这证明了本文模型在本文所研究工装模型的有效性和优越性。
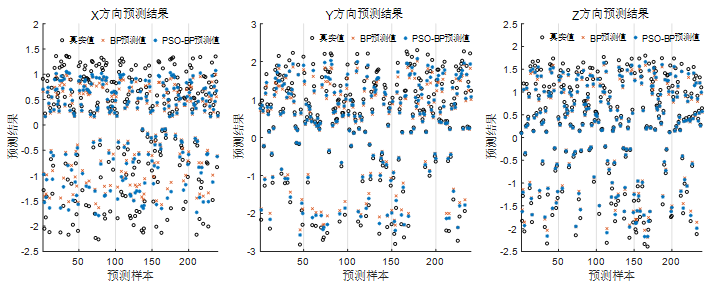
图1 计算结果对比
4 结论
本文所提出的大型工装基准点热漂移优化代理模型,与BP神经网络构建的模型进行对比后表明在各方面均有提升,利用实际采集的漂移数据得出本文模型平均相对误差百分比均在22%以下。










