引言
伴随着信息技术及图像处理技术的迅猛发展,在对图像进行压缩、去噪以及重构等图像处理时,有效的图像稀疏化表示法对重构图像质量的影响非常关键。因此图像稀疏化表示是图像处理环节中的一个不可或缺的步骤。
所谓信号的稀疏表示是指将信号投影到正交变换基时,绝大部分的变换系数的绝对值都是很小的,得到的变换向量是稀疏的或者近似稀疏的,可将其看作对原始信号的一种简洁表达[1]。为了简化模型,设定一个N×1的离散实值信号X,X中的元素为,其中n=1,2,…,N。如果X在正交基Ψ上是稀疏的,也就是有K个非零系数时,那么X可以用Ψ的列向量K阶稀疏表示,写成矩阵形式为:
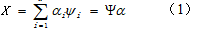 (1)
(1)
其中α是N×1的矩阵,Ψ是N×N的矩阵,Ψ称为X的稀疏基。
在大多数的情况下,信号X不可能完全满足严格稀疏的这一要求,即在稀疏基上只有K个非零元素,其余的元素都为零。如果信号X的变换系数经过重新排列之后是以指数形式衰减的,直至趋于零,说明这个信号仍然可以压缩,也就是可以近似稀疏的表示该信号[2]。理想情况下,在可以不失真的恢复原始信号的前提下,我们希望信号的稀疏个数K越少越好,这样就可以提高我们的采样速度以及减少传输、存储时所占用的资源。所以选择合适的稀疏基Ψ是关键,一般比较常用的稀疏基主要有FFT变换基、正余弦变换基、小波变换基、冗余字典等。
小波变换使用“正方形”结构作为其支撑区间,不具备方向性和各向异性。小波的多分辨率用不同大小的正方形来描述,当分辨率足够高时,小波就近似用点捕捉图像的轮廓信息[3]。而Contourlet变换使用和轮廓段类似的基结构来更好的逼近图像,它的基函数分布在多尺度多方向上,使用具有随尺度而变化特性的“长方形”结构作为其基的支撑区间[4]。Contourlet变换系数中,能量更加集中于表示图像边缘轮廓的系数,所以,Contourlet变换仅仅使用少量的系数就可以更有效地来捕获自然图像的主要特征,因此可以使图像得到“稀疏化”表示。图1.1表示两种变换分别对同一曲线的描述。小波变换的正方形结构对曲线的刻画如图(a),Contourlet变换的长方形结构对曲线的刻画如图(b)。
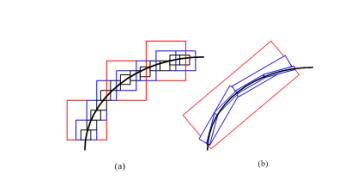
图1.1 两种变换分别对同一曲线的描述
Contourlet变换的基本思想可以分为两个步骤:
(1)捕获边缘奇异点。选用拉普拉斯塔式滤波器结构(Laplacian Pyramid,LP)捕获二维图像中的奇异点,它是获得对图像进行多分辨率分解的有效方式之一。LP分解将原始信号分解产生一个低通采样逼近和该图像与低通预测图像的差值图像,即高频分量[5];对分解得到的低频分量再进行LP分解以得到下一层的低频分量以及高频分量,以此类推,循环进行下去。最后就得到了图像第n层的低频信息和n个高频信息,从而获得了图像的多分辨率分解。LP的优点是它对每一层的分解都将这一层的图像分解为高频子带部分和低频子带部分。缺点是不具有方向性。
(2)根据各方向信息把位置比较相近的奇异点连接成轮廓段。对于由LP分解得到的每一层的高通子带部分直接输入到方向滤波器组(DFB)中进行方向分解,如果DFB对图像进行n个方向分解,在任意的尺度上能够得到的方向子带数为2的n次方。DFB通过把奇异点逐渐汇聚成线形结构来获得图像的轮廓信息。DFB的优点则是对于高频子带部分的处理更加优秀,缺点是对低频部分的处理效果不好。
塔形方向滤波器组(PDFB)是由LP和DFB结合而成的,Contourlet变换采用LP与DFB结合的塔形方向滤波器组(PDFB),因此也就结合了LP与DFB的共同优点,弥补了LP与DFB的不足之处。图1.2给出了Contourlet变换的PDFB结构图。
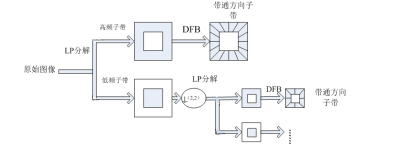
图1.2 Contourlet变换的PDFB结构图
3.Contourlet重构
Contourlet重构是Contourlet分解的逆过程:
(1)对输入的最顶层的高频分量进行DFB重构;
(2)将DFB重构后得到的系数与最顶层的低频分量进行LP重构,并将其输出作为下一层的低频分量;
(3)对次高层的高频分量进行DFB重构,将得到的系数与步骤2)输出的低频分量进行LP重构,再输出下一层的低频分量。重复以上步骤,直到得到与原始图像大小相等的重构图像,重构图像过程结束。
4.结论
本文选用Contourlet变换对信号进行稀疏化处理。Contourlet变换只需要少量的系数就可以捕获自然图像中的边界轮廓信息,而这些信息正是图像的主要几何特征,因此Contourlet变换能稀疏的表示图像。
[1] 练秋生,陈书贞.基于解析轮廓波变换的图像稀疏表示及其在压缩传感中的应用[J].电子学报,2010,38(6):1293-1298.
[2]张壮. 基于稀疏表示的图像去噪与融合技术研究[D].南京理工大学,2020.DOI:10.27241/d.cnki.gnjgu.2019.000335.
[3] 岑翼刚,陈晓方,岑丽辉,等.基于单层小波变换的压缩感知图像处理[J].通信学报,2010,31(8A):52-55.
[4] 易文娟,郁梅,蒋刚毅,等.Contourlet一种有效的方向多尺度变换分析方法[J].计算机应用研究,2006,9(20):18-22.
[5] Cunha A L,Zhou J,Do M N.The Nonsubsampled Contourlet Transform:Theory,Design,and Applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.










