一、问题提出
高三的一轮复习主要是帮助学生梳理基础知识，训练基本技能，通过基本活动经验认识其中蕴含的数学思想。那么如何定位二轮复习呢？尽管利用专题进行二轮复习已成为广大教师的共识，也是主要教学形式，但在实际操作中，老师经常是把之前学生的错题再讲一遍，往往是“炒冷饭”，没有延展性，系统性。学生也面临“瓶颈”，总是大量刷题，但思维能力提升不大，思路还是打不开。笔者认为二轮复习的定位应该是这样的：重视活动经验的激活与重组，促进有效联想，从不同角度“翻译”条件和结论并搭建它们之间的桥梁，从而认识问题，理解问题本质，提高分析解决问题的能力。袁振国先生曾说过：研究性教学不仅是重要的教学法，也是日后继续独立学习、独立处理问题的生活能力的重要保证，而且是以学生发展为本的价值追求。这与在普通高中数学课程标准(2017)提出“立德树人”的目标是一致的。本文结合笔者执教的一节圆锥曲线定值问题探究课，谈谈自己的思考，不足之处，敬请批评指正。
二、.试题探究过程
尽管每个老师在一轮复习中对解析几何都进行了很多专题的教学，学生也慢慢不再畏惧，但对一些非常见或计算量大的问题，学生要么无从下手，要么决策失误，导致有想法但路途坎坷，不能在有限的时间内完美解决。本文是我们在二轮复习期间的周练讲评课，是解析几何中常见的定值问题。本题的基本反馈是：大部分同学将题目中的距离“翻译”成点到直线的距离，所以基本思路都是设直线方程然后表示距离。但是学生在二轮复习期间的做法是其本人进行方法选择的结果还是仅凭印象不由自主地使用方法？如果是前者，那么当问题改变或被“化妆”变脸，经验不再适用时怎么办？这就是在基本活动经验上的新的增长点。
（1）求椭圆C的方程；（解答过程略）
（2）设点M、N为椭圆C上的两个动点，问：点O到直线MN的距离d是否为定值？若是，求出d的值；若不是，请说明理由。
【教学片断1】分析结论，赋予结论不同的身份，让新活动经验生根发芽。
师：本题的问题是什么？
生：点O到直线MN的距离d是否为定值。
师：如何定义d的身份？
生：d是点O到直线MN的距离。
师：还有其它身份吗？
学生沉默
师：如果我设O向MN做垂线的垂足为H，,你会想到什么？
生：哦，d是直角三角形斜边上的高！
师：非常棒！一点就通！那你还有其它想法吗？
生：我觉得这种题目一般结论都是定值，如果是定值的话，说明垂足H的轨迹是个圆，那我只要证明点H的轨迹是个定圆就可以说明d是定值了。
师：此处应有掌声！
【设计意图】全国Ⅰ卷高考试题中解析几何解答题一般在20题的位置，难度比较大，如果方法选得不好，即使有思路也很难在规定时间内完成。所以对于题目结论的分析尤为重要！路选对了，走起来就比较平坦顺畅。本题中同学们往往忽略了d作为直角三角形斜边上的高这一身份，通过极坐标和等面积法证明d为定值对于本题来说也是一个运算量不太大的比较好的选择。
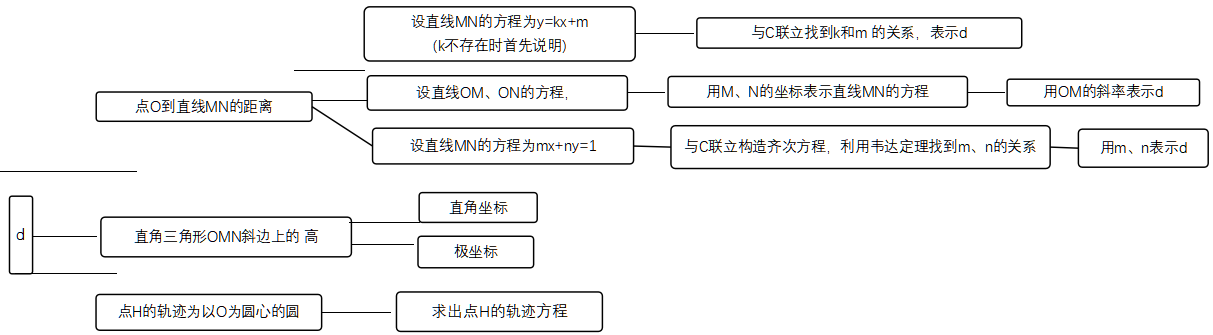直接求点H的轨迹方程会更加简化运算。
【教学片断2】分析条件，确定具体解题思路和步骤，让新活动经验茁壮成长。
师：那你打算具体怎么操作呢？请小组进行讨论
代表1：d是点到直线的距离，所以要先写出直线方程，当直线斜率不存在时单独计算，这个值也是将来我们要证明的定值。斜率存在时，可设直线方程为y=kx+m，d用k和m表示，由,利用韦达定理可得k和m的关系，然后代入d即可。
师：考虑全面，叙述准确条理，非常好！
代表2：也可设直线OM的方程为，直线ON的方程为，分别与椭圆方程联立求出点M、N的坐标，然后表示直线MN的方程，进而求出d的表达式，只含有k一个参数。
师：有补充的吗？比如k？
代表2：哦，当直线OM和ON一个斜率不存在，一个斜率等于0时，单独说明并求出d的值。
师：很好，由点写直线方程，只含一个参数。
代表3：我们前面和代表2一样，先求出M、N的坐标，然后求出|OM|和|ON|的值，再利用等面积法表示d.
师：不错，利用了d的第二个身份。
代表4：由，我们想到设直线MN的方程为mx+ny=1，与椭圆方程联立，构造关于x，y的齐次方程，再利用韦达定理得到m，n的关系，后面和代表1相同。
师：非常好！他（她）们想到了齐次方程。还有吗？
代表5：我们想先求出点H的轨迹方程。
师：很好，这是一个基于猜想基础上的全新的想法。
【设计意图】分析了题目的结论之后就需要分析条件，如何利用条件？如何与结论建立起关系？开放式的引导，让学生尽情放飞思维想象的翅膀。陈省身说过：数学是自己思考的产物。首先要能够思考起来，用自己的见解和别人的见解交换，才会有很好的效果。再者每个同学的活动经验是不一样的，根据皮亚杰提出的认知冲突理论，学生自己的方法和同学的想法产生了冲突，这样就积累了新的活动经验。
【教学片断3】实际操作后，沉淀反思，让新活动经验开花结果。
师：刚才几位同学基于自己小组的活动经验得到了几种不同的可行性方案，并就具体过程进行了展示，你认为哪位或哪几位是最好的？
生1：我觉得法1最好，计算过程不算复杂也好想，法2、3计算量有点大，法4我想不到，而且如果改变O点就不能用这个方法了。法5对我来说是最新颖的，过程也比较简洁，之前只会猜定点和定值，没有想到定值还有其它的解释。
师生大笑
生2：我挺喜欢构造齐次方程的方法的，利用韦达定理来体现垂直，多奇妙啊！
师：“一千个读者就有一千个哈姆雷特”，这就对了！所以我们一定要多思考，多联想，然后选择最适合自己的那一个。不过刚刚提到的法4如果不是坐标原点引出的两条直线就不能用了吗？
生2：可以平移到坐标原点。
师：对，可以平移，看来他确实“喜欢”齐次方程！那么还有其它途径来表示吗？
学生沉默
师：|OM|的长其实就是点M的……
生：哦，极径
同学们豁然开朗，继续补充可以通过极角来体现条件中的垂直。
师：非常好！我们往往在做选做题时才会用到极坐标方程，所以思维受到了一点限制。那么说了这么多的方法，你有什么收获呢？
生：要从不同的角度去翻译题目中的条件和结论，并建立它们之间的联系，然后选择最优方法。
生：我想推一个一般性的结论，就是将椭圆方程一般化，垂直条件不变，找到d和a，b的关系。
生：我想把它推广到双曲线和抛物线。
师：好！知道举一反三了，这些问题我们可以继续研究。也许你会有新的发现！
【设计意图】“学而不思则罔，思而不学则殆”，不思则无，深思则远，远思则宽。解题反思应贯穿于整个解题活动之中。经常让学生经历这样的活动经验，学生自然就会主动思考、总结并进行拓展了，这样做看似很耗时，却起到了举一反三的效果，实际事半功倍，同时增强了学生面对“难题”时的信心。
. 数学学习是新旧经验反复的、双向的相互调整和累积，最终内化并增值成数学素养的过程。.数学经验是数学素养“养成”或“生长”的“土壤”，数学核心素养最终落实到数学活动经验上。数学活动经验是指个体在数学活动中经过心智操作和心力操作过程后储存于长时记忆系统中具有意义和价值的数学信息。.因此，数学经验的获得是心智和心力协同作用的结果，数学经验的获取过程就是数学核心素养的生成过程。数学问题解决经验和数学思维经验都是滋养数学核心素养的活水，缺乏丰富数学思维经验的人，很难说他具有良好的数学核心素养。但数学经验过于丰富也可能导致“经验主义”，而使数学核心素养降低。比如，对学生已经理解并掌握了的数学知识再大量反复操练，就会导致“孰能生笨”“孰能生厌”，就会出现经验过剩但素养下降的情况。这说明，过度训练导致经验的过度积累，并不利于素养的提升。所以在二轮复习中，教师一定要充分了解学生，对于不会的不熟练的内容要舍得花时间并设计有效的探究问题让学生充分联想，体验整个解题过程。这样做看起来比较耗时，殊不知经常进行这样的思维训练，学生才可以通过基本活动经验提升自己的数学思维能力，提高数学核心素养，是个一本万利的做法。数学教育的根本在于立德树人，高三数学的二轮复习也应以生为本，不断优化教学举措，突出学生的主体地位，突出数学本质，突出高考指向，从“大观念、大主题、大单元”的角度组织教学内容，不断提升学生的核心素养。
参考文献：
叶琳. 重激活 善转换 勤反思——高三二轮复习课的实践与思考 高中数学教与学，2020（10）
赵思林，高峥，熊露. 数学核心素养的内涵探究. 高中数学教与学，2020（10）
李国林. 积累活动经验 培养学科素养——由《直线在椭圆中定点问题探究》的教学片段谈二轮复习 中学数学研究. 2020（8）
【作者简介】贺晓霞，山西省榆次第一中学校.
