引言：
现代飞机为实现通信、测控、预警等目的，往往需安装相应功能的雷达天线，为保护这些雷达天线不受飞机外部环境的干扰和破坏，需在天线外部设计、安装相应的天线罩，使雷达系统在复杂多变的环境中正常工作。天线罩的出现是在1941年，其最初的主要功能就是外形整流以及保护天线结构系统，但是今天的天线罩结构已经需要具备多种功能，如透波性能、刚度性能、强度性能、外形的气动性能等，现代天线罩结构已经成为集多种功能于一身的复合构件[1]。
天线罩在满足透波性能和强度性能的前提下，为适应日益提高的减重需求，往往伴随着刚度的降低、变形的增大，从而导致变形后的外形气动性能降低[2]。而天线罩的大变形特性则导致工程上常采用的线性静力分析方法所计算出的天线罩变形量往往与实际变形相差较大，对飞机气动性能影响的评估易产生较大偏差。为准确预测天线罩变形量，本文尝试采用非线性分析与简化接触约束的分析方法加以计算，并辅以静力试验的变形测量进行验证。
1.几何非线性与接触约束
线性静力分析是最基本的力学分析过程，在一定的理论假设和误差范围内，大多数实际问题都可以简化为线性问题。这些假设通常包括：小位移假设、弹性假设、连续性假设等等。但是实际问题包含了更广泛的影响因素，在更多情况下，需考虑材料的屈服和硬化，或者结构发生了大位移，刚度矩阵必须更新才能得到正确结果，此时，非线性分析就非常必要。
一般工程结构问题中的非线性问题分为三类：几何非线性、材料非线性和边界条件非线性。在工程上，复合材料结构通常按照损伤容限要求设计，在使用载荷范围内，材料仍处于线弹性范围内，因此无需考虑材料非线性。本文所研究的天线罩变形问题主要涉及大变形的几何非线性和接触约束的边界条件非线性。
几何非线性问题的基本有限元求解算法为全牛顿-拉弗森（full Newton-Raphson）算法，在每个增量步内，全牛顿-拉弗森算法迭代求解如下方程：
当求解满足收敛条件时，迭代终止，进入下一个增量步。常用的基本收敛准则有残差收敛准则、位移收敛准则和应变能收敛准则等。
在接触问题中，产生接触得两个物体必须满足无穿透约束条件，即：
(6)
式中——变形体增量位移向量；n——单位法向量；D——接触距离容限[3]。
从力学分析的角度看，接触是边界条件高度非线性的复杂问题，是一类特殊的、不连续的约束。在实际计算中，接触问题往往伴随求解不收敛的问题，如果能将非线性的接触约束简化为线性约束，将大幅提高实际工程中的计算效率。本文中也将尝试使非线性的接触约束简化为线性的类接触约束，以提高计算的效率。
2.工程算例
典型圆盘形天线罩的连接形式如图1所示。天线罩通过单排螺栓与安装支架连接，天线罩在飞机的飞行过程中承受法向向外的气动载荷。经过风洞试验的测试，共给出9种不同的飞行姿态的气动载荷。再通过对比不同工况下天线罩上下表面的合力、合力矩，本文挑选出其中最严重的两种载荷工况加以计算、验证。其中工况Case1为天线罩上下表面总载荷绝对值之和最大的工况，工况Case2为天线罩总弯矩最大的工况。
由于天线罩为次承力结构，通常通过一排螺栓将天线罩与支架相连接即可满足强度要求。采用这种连接方式，罩体在承载时，罩体和支架的连接边之间存在接触问题，导致实际约束方式介于简支约束与固支约束之间。
为避免非线性的接触约束，本文提出以下简化约束方式：在罩体螺栓连接点（如图2 B点）处简支约束；罩体外缘（如图2 A点）限制沿罩体外表面法线方向的位移；罩体连接边内边界点（如图2 C点）不加约束，使其能够自由向外位移。本文将以上简化约束方式称之为类接触约束。
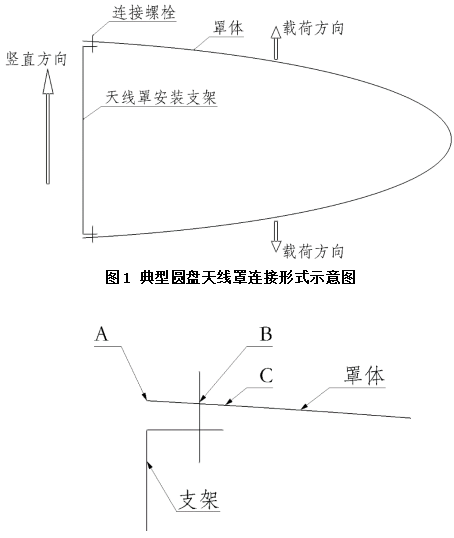图2 罩体连接局部典型示意图
3.计算结果与试验验证
采用Abaqus有限元软件针对上述天线罩在不同工况、不同求解模块、不同约束形式下的变形情况加以计算，结果如表1。
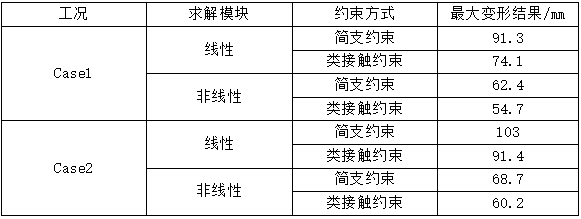表1 有限元变形仿真计算结果
为验证计算结果，设计并实施了天线罩静力试验，通过拉压垫-杠杆系统施加外表面压缩载荷，加载示意图见图3，采用胶布带-杠杆系统施加外表面拉伸载荷，加载示意图见图4。
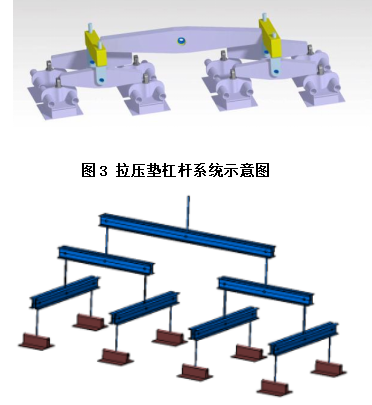图4 胶布带杠杆系统示意图
经过试验测试，工况Case1最大位移为48.05mm，工况Case2最大位移为60.93mm，仿真计算与试验的误差如表2所示。从表中可知，非线性模块+类接触约束的计算结果最准确，两工况下误差分别为13.84%和-1.2%；而工程上最常采用的线性模块+简支约束计算出的变形结果误差最大，两工况下误差分别为90.01%和69.05%。两工况下，采用非线性模块+类接触约束的计算方法可将计算准确度提升约70%~80%。
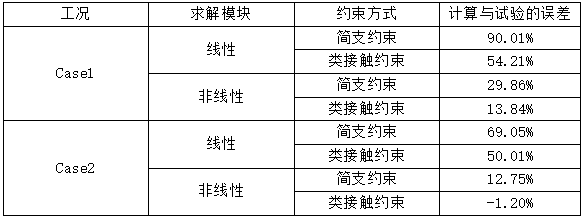表2 仿真计算与试验的误差
4.总结
当飞机天线罩在减重的同时，其刚度逐渐变弱，这导致工程上常采用的线性静力分析与简支约束逐渐不再适用。为准确预测天线罩变形量，本文尝试采用非线性分析方法与类接触约束结合的方法计算天线罩变形量，并辅以静力试验的变形测量进行验证。
经对比，采用非线性分析与类接触约束分析方法相比线性分析与简支约束分析方法可提升计算准确度约70%~80%，这种分析方法可为类似的工程分析提供一定的参考。
另外，同样采用非线性分析与类接触约束分析方法，两种工况下的计算误差却相差较大，原因可能与试验件约束方式有关，具体仍有待进一步探究。
参考文献：
[1]史强.机载雷达罩复材夹层结构强度设计与分析[J].内燃机与配件,2018(21):181-183.
[2]刘捷,赵志斌,陈志刚.大型机载雷达罩结构设计[J].电子机械工程,2003(02):1-2+44.
[3]杨剑,张璞,陈火红.新编MD Nastran有限元实例教程[M].北京：机械工业出版社，2008.
