引言:数学知识是较为抽象的理论学科内容,在高中生的学习过程中,单凭个人想象以及计算很难对日益深奥的数学问题进行深入的理解。传统的理论讲解模式,单一的题目解决方式讲解已经不符合现阶段的教学理念,不利于学生数学思维的发散。尤其是高中数学内容较为深奥繁琐,在学生学习、解题过程中会使用到大量的计算,需要高中生根据题目的表述理解较为抽象的数学问题。文字的描写和学生的想象不足以让学生明确数学题目的内容和后续的解题步骤等。对此,可以开展数形结合的教学应用。在数形结合教学过程中,可以提升高中生的解题能力,深化高中生对于题目的理解,减少相关的计算,提升题目答案的准确率。
一、数形结合在集合中的应用
《集合与常用逻辑用语》是高中人教版必修一的内容,作为高中生在高中阶段学习的首个数学知识,集合是非常重要的。高中阶段的数学知识点较为繁琐、深奥,集合也有着这样的特点。在高中生学学习集合的过程中会遇到较难的题型,传统的解决方式,经常会伴随着大量的计算,加大的提升了高中生的计算错误率。对此,在高中生开展集合的学习过程中就可以带入其数形结合的应用,使其集合题目的表达更加直观,清晰。
例如:已知集合A=,集合B=,要求的这两个集合中主要有多少个相交的元素。在高中生刚刚接触集合问题时,遇到此种问题会找不准具体的解决方法。如果使用常规的计算方式,高中生将两个等式联立之后会发现其整体的计算量较大,在考试中比较浪费时间。针对此种集合问题,高中生可以开展数形结合的运用,我们可以根据集合内的等式发现,集合A和集合B分别表示圆的公式以及抛物线的公式。学生可以利用公式的表示将具体的图像在象限中表示出来,以此来得到两个集合所共同包含的元素个数,解决具体的集合问题。利用数形结合的方式解决高中的集合问题,可以减少大量的计算,提升高中生的做题效率和准确性。
二、数形结合在函数中的应用
数学知识中函数的学习一直贯穿于整个高中学习,是非常重要的内容。在必修一中学生会接触到一元二次函数、函数的概念、函数的应用等,需要高中生可以根据函数的题目,有正确的解题思路,完成相关数学问题的作答。函数的问题过于抽象,凭借学生的空间想象能力很难全面的了解问题的全部过程,得到最终的解决方式。基于函数问题的特点,在学习函数过程中数形结合的应用是非常重要的。在高中函数的学习过程中,可以利用数形结合的学习模式,根据函数的解析式,得到函数的图像,从而解决对应的函数问题。
例如:在高中阶段学习的三角函数内容,正弦余弦的变化情况,教师都会让学生对于变化的图形进行记忆,直观的图形更有利于学生的记忆和了解。正弦公式:y=Asin (ωx+φ)+k,其图像表示如图一所示。学生可以根据正弦公式的图像结合后续的方程式得到函数直观的图像表示,对于函数的奇偶性、单调性、特殊点等数据快速的了解。例如:已知方程y=sin (8x+3)+5在(0,2)内的最大值和最小值。可以根据方程的表达绘制相关的正弦图像,确定其图形的单调性,在确定在(0,2)范围内的最值问题。
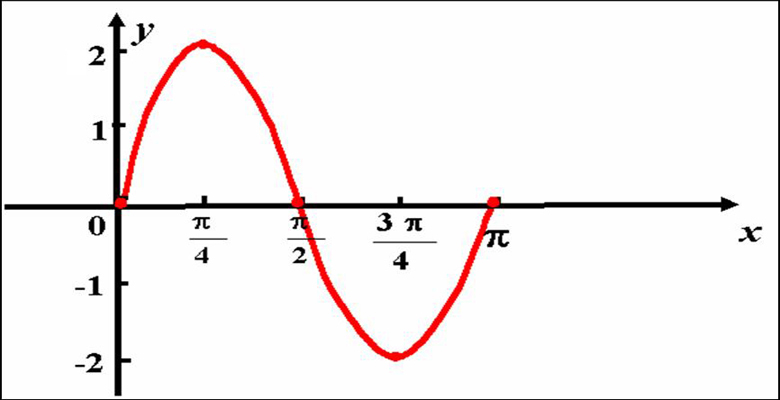
图 1正弦函数图像
在高中学习过程中,函数的内容会逐渐加深,不断的增加难度,高中生如果对其数形结合的运用足够熟练,可以提升自身的数学思维,提高自己的解题效率。数形结合的运用在函数求零点时也有着较为明显有效的运用。例如:已知e是自然对数的底数,f(x)=mex+x+3,设m<-e2,求证函数f(x)没有零点。这道函数零点问题较难,学生单凭计算很难沥青具体的思路,完成题目中所提的问题。对此,高中生,可以将函数f(x)的图像绘制出来,根据图像中交点位置,对其不同的区间进行探讨。讨论x在不同的范围下,其零点的个数。
在函数的学习过程中,数形结合是较为有效且一定会运用到的方式,可以有效的提升高中生的做题准确率。也使得高中生在函数图像的直观显示下,可以更加清晰的了解数学的题目内容,了解函数的取值范围,以及讨论范围等。
三、数形结合在立体几何图形的应用
在高中数学的学习过程中函数学习中,数形结合的应用较多。在高中立体几何图形的学习,数形结合的应用为主要的学习方式。高中人教A版必修二的教科书上,在第八章对立体几何图形进行了详细的讲解。其中包括《基本立体图形》、《立体图形的直观图等》,以及更加深入的空间直线、平面之间的位置关系等。需要学生在直观的图画表示下理解立体几何的题目,并开展后续的问题解决。
例如:在立体几何图形的实际问题中,一块木板如图所示,点p在平面VAC内,需要过点P将木板截断,并且需要保证界面能够平行于VB与AC之间,请问具体的截法如何在木板上画线?(问题图形表示如图二)在立体几何的问题中,类似于此类的实际问题较多,大部分立体几何的问题都需要高中生结合直观的图画来进行解决。直观的图画可以让学生更加清楚的了解到题目中所描述的图形特征、图形概念,并且根据图画上的表示,解决相关的问题。由此我们可以发现,数形结合的应用在高中立体几何图形的学习过程中必不可少,可以确定其为主要的学习方式,需要学生有着较好的数形结合运用能力,根据题目所给出的条件,解决相关的立体几何图形问题。
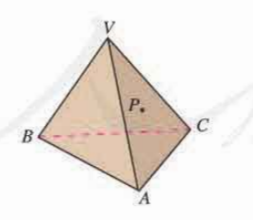
图 2立体几何中的实际问题
结束语:综上所述,数形结合的思想在高中数学的教学过程中有着极高的应用价值和良好的教学效果。教师可以根据实际教学内容提升对于数形结合的教学应用,使学生更加深入的了解数学题目,减少学生答题的时间,提升高中生的做题效率,保证数学课堂的教学质量。本文从集合、函数、立体图形这三个方面对数形结合的应用进行讨论。希望在本文的论述下,可以提升高中数学工作者对于数形结合思想的重视。以数形结合思想为基础,开展整体的高中数学教学。希望我国高中生在教师的帮助下以及高中生自身的努力下,能够让学生提升自己的数学成绩,促进我国高中数学教学的发展和进步。
