在电网的设计中，电力系统的短路计算是一个必不可少的步骤。目前，由于新能源电源机组在电网中所占的比例显著提高，因此其短路电流特性也随之发生了很大的改变，通常无法再采用传统的对称分量法等进行计算。显然，为确保计算结果能够更好反映实际结果，就应当进一步加强研究，以确保实现对现有的短路计算方法进行改进，满足实际工作之需。
1新能源电源接入不平衡配电网的短路计算模型
考虑到实际情况，在本次计算中选择DFIG短路计算方法进行计算与相关设计，DFIG的短路电流特性与Crowbar能否激活具有一定关联。所以结合实际需求对Crowbar能否完成激活进行分析，要设计搭建短路计算模型。
经分析后发现一旦Crowbar不处在激活状态当中，该电路中产生的故障电流影响主要源自低电压穿越方法的选择，同时，在这种情况下，DFIG短路电流中并不包含负序分量，因此只对其正序分量进行分析即可。基于此，该故障电流的正序分量如下：
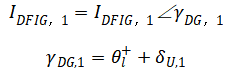
其中，
和
分别为故障电流正序分量的幅值和相角，
则为定子电流在正转同步速旋转坐标系下各坐标轴分量之和。在以上算式中，引入
的主要原因是，本次新能源电源采用的是定子电压矢量控制方案，因此必须引入
这个参量，才能有效表示正序电流
在复平面中的实际相角。
而当新能源电源接入不平衡配电网而引发严重的电网故障时，发电机当中的转子产生电流冲击与母线发出的电压会超过Crowbar设备的激活定值，同时，要保证该转子换流器可正常稳定运行，Crowbar设备当中的配置开关此时会快速导通，同时Crowbar会发生短接，另外转子电流则会经过Crowbar设备，最终Crowbar才会被真正的激活。Crowbar在激活状态时，该电网中故障电流同Crowbar非激活状态当中故障电流存在着明显的区别，已不能沿用以往的模型，现在则需重新构建设计短路计算模型。
该特定环境条件中，DFIG自身稳态基频中的分量与异步电动机中的等效模型需吻合，所以DFIG在特定环境中正、负网络等值阻抗如下：
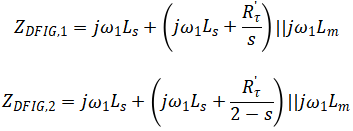
式中，
和
主要是DFIG在网络中正序、负序的等值阻抗表现；Lm表示转子漏抗，
为转子绕组等效电阻，
为工频频率，s为转差率。
2故障前相分量节点导纳矩阵的建立
在建立该矩阵前，要对电网内各个电力元件进行分析，明确故障前各分量节点之间的三相导纳，在获知各节点的三相导纳之后，即可以此类推，建立相关的3×3阶矩阵，矩阵如下：
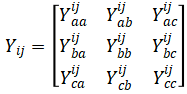
在该矩阵中，i和j为节点号，ab则指的是节点i和j在a相和b相之间的导纳，以此类推。
3新能源电源相分量模型的构建
从目前来看，在新能源电网组网当中，如出现电网故障，则多会导致DFIG的Crowbar激活。在这种情况下，电力系统中的DIFG则可等效为异步电动机模型，此时相分量短路计算模型即可用以下公式加以表示。
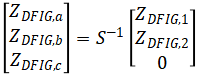
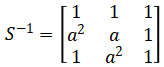
在这两个公式当中，ZDFIG包括的a，b，c主要为DFIG在电网当中的a，b，c三相等值阻抗；该表达式中1、2表示DFIG待Crowbar实现激活后的正序、负序的等值阻抗。根据以上两个公式进行计算，即可分析出对应的控制策略，并对DFIG的相分量短路计算模型加以修改。
4配电网故障时的节点电压方程
经分析后发现Crowbar设备的激活效应可影响到DFIG故障电流特征。因此，在短路计算之前，需要根据电网短路计算的实际情况，判断Crowbar装置是否激活[1]。如发现为Crowbar装置已经激活，则要以此为基础，建立双馈型电源相分量短路计算模型，并对电网相分量节点的导纳矩阵进行重建[2]。否则，不用实现改变或重设导纳阵型，也无需按照构建模型对励磁控制方法进行分析，另外要对短路计算方式进行侧重分析、方法研究，构建设计更为科学实效的模型应用方程。
当然，在新能源电源接入不平衡配电网以后，其馈出的故障电流正序分量与负序分量等均与机组并网点的节点电压之间存在非线性关系，显然，仅凭相分量节点电压方程很难进行快速准确的解析计算[3]。另外需对电网电压计算方程进行优化设计，让其能够与短路计算方式可协同应用、配合开展，实现迭代计算应用求解，实现对含新能源机组接入的不平衡配电网进行短路计算[4]。具体如下：
第一、实践应用中必须结合实际参数，对相分量节点方程形成步骤给予设计明确，之后开展导纳矩阵与电压计算方程应用。
第二、对已经衔接的新能源电源真实情况进行分析，对何种类型进行判断明确。
第三、以双馈型电源为例，对Crowbar装置激活状态进行判断明确，如处在激活状态，可选择DFIG中的Crowbar保护动作完成后的相分量等效模型出现的节点导纳矩阵与电压方程,如非处在激活状态，要按照低电压穿越方式，设计相分量故障计算等值模型。
第四、在该过程中结合实际故障类型，同时修改相分量节点导纳矩阵、电压计算方法。并以迭代计算方法应用为主，对相关电流数据与数值信息进行快速获取，实施当中要充分考虑其故障问题、故障形式，例如在故障点A中，经调查分析后发现，各相电压值皆为零，此时关联电流的变化动态与其系统或相关衔接点电势紧密关联，在对电流源输出进行分析判断中可以衔接点电势为基准。在研究案例中选择两相接地故障，通过对该故障进行分析后，得到最终的节点电压表达式如下。
再对此公式进行迭代计算，即可逐步求出每条支路的各相电流值。当然，为确保迭代计算结果收敛，可采用故障前电流作为第一次迭代值。
第五、对各节点相电压中的二次迭代值进行分析判断，以是否达到迭代精度为判断标准，如没达到，需对迭代结果进行计算等值模型引入，重新开始迭代，如已达到则可开展下一步骤实施。
第六、在节点电压数值计算中也可应用迭代求解方法，完成电流分量的计算求解，以实现故障电流计算的最终目标。
综上所述，通过对新能源电源介入接入不平衡配电网中的短路计算方法进行研究，本文提出具有可行性的方案与应用方法。随着我国新能源产业逐渐兴起，电源供应保障及安全可靠越发备受关注，本次研究从实际应用层面对诸多问题给予阐明，并为电网稳定运行及安全保障提供参考。
结束语：总的来看，面对现有的电网对称分量法难以满足实际需要的情况，研究新的短路计算方法也已是大势所趋。当然，本次研究也难免存在一些局限，为此，在今后的研究中，将更侧重于电网安全运行方面的要素。
参考文献
[1]谢瑞.含分布式电源配电网故障特性分析与保护方案优化研究[D].南昌工程学院,2020.
[2]孙充勃,李敬如,罗凤章,等.考虑分布式电源接入的配电系统典型算例设计[J].电力建设,2020,41(10):47-62.
[3]李芳,程相刚.典型配置下分布式新能源优化配置[J].农村电气化,2020(08):54-56+79.
[4]韩佳.小容量分布式电源接入配电网的优化决策研究[D].青岛大学,2020.