引言
在力学问题中,求解动力学时,既可以用牛顿定律求解,也可以用动能定理求解。无论物体所受的力是变力还是恒力,动能定理都是适用的。在一般的动力学问题中,两种方法都可以求解。下面分别介绍两种方法求解动力学问题的一般步骤,并具体举例说明解题过程。运用动能定理解某些动力学问题时,比运动牛顿第二定律要简便。
1牛顿定律求解动力学问题
运动牛顿第二定律解题时一般按照如下步骤(1):
(1) 选择合适的研究对象。若有几个物体,则对每个物理进行分析。
(2) 分析研究对象的运动状态,如:速度、加速度等,若有几个物体,还需找出它们之间的关系,即找到描述它们运动状态的物理量之间的联系,如:位移、速度和加速度等之间的关系。
(3)分析每个研究对象的受力情况。
(4)根据牛顿第二定律把描绘物体的物理量,如:质量、速度、加速度、受力等联系起来,列出方程,再根据已知条件,求解方程。
(5)最后对问题进行分析讨论。
2 用动能定理求解动力学问题
合外力所做的功等于动能的增量,这个就是动能定理,它是牛顿第二定律的一种积分形式(2)。运用动能定理解动力学问题时一般步骤如下:
(1) 确定合适的研究对象。研究对象可以是一个物体,也可以是几个物体组成的系统。
(2) 对研究对象进行受力分析,再确定物体的运动情况。
(3) 根据动能定理列方程求解。
3举例
有一细棒用细绳悬挂,细棒的下端在液体下面。现将悬绳剪短,求细棒完全浸入液体中时细棒的速度。设细棒和液体的密度分别为P和![]() ,细棒的长度为L,假设液体没有粘滞性。
,细棒的长度为L,假设液体没有粘滞性。
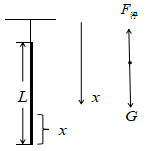
图1
解法一:运动牛顿第二定律求解
建立如图1所示的坐标,设细棒浸入液体中的长度为x,所以 (1)
(1)
以细棒作为研究对象,根据牛顿第二定律可知: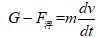 (2)
(2)
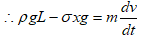 (3)
(3)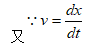 (4)
(4)
将(4)代入(3)中可得,![]()
上式两边同时积分,![]()
![]()
解法二:用动能定理求解
在细棒下落的整个过程中,合外力所做的功为:![]()
在这个过程中,动能的增量为![]()
由动能定理可知,![]()
所以,![]()
4结论
综上所述,同一个力学问题用牛顿定律和动能定理求解结果完全相同。动能
定理是从牛顿第二定律推导出来的,在一般情况下,若能用牛顿定律求解动力学
问题,都可以用动能定理求解。另外,用动能定理比用牛顿定律解力学问题过程
简便很多。
[参考文献]
程守洙,江之永 主编,胡盘新,汤毓骏,钟季康 修订.普通物理学(上册)第六版[M]. 高等教育出版社,2006年12月第六版.
[2]韩家骅,汪洪 主编.大学物理学[上册]第3版[M].安徽大学出版社,2015年1月第3版.
作者简介: 韩莲芳(1982- ),女,安徽省池州人,汉族,博士研究生,副教授。研究方向:量子光学与量子计算。





