可靠性分配是权衡过程，在优化系统设计时，应考虑其他约束，如成本效益。在可靠性分配过程中，原则应适当适应实际情况，特别是在约束处理过程中，分配原则可根据实际情况进行扩展。承制方可以在低水平上灵活分配系统中的指标，只要这些指标能够在相互补偿的基础上满足系统要求。如果总分配指数超过了技术开发水平和相关成本的实际数量和质量要求，应按照相关程序修改总分配指数或其他限制。目的分配结果在技术上合理、经济、见效快。
一、可靠性管理在航空维修分析
在飞机运行期间，以不断持续结构、系统、部件和发动机的可靠性数据。一是提高数据收集的准确性，完善数据收集和处理流程，处理标准，严格收集和信息记录，完善所有信息的审查和验证流程。提高信息的准确性。二是维护信息收集的完整性。信息的完整性对于确保信息流不会中断或丢失至关重要。信息的内容和数量必须完整，数量的缺乏往往使人们难以研究信息的规律；数量也是补偿个人数据失真的有效手段。没有准确、及时和全面的数据收集，就不可能保证后续行动和结果的准确性。事实上，这些数据是不完整和不准确的。这可能是因为首先，事实上，填写问卷的员工没有正确填写，可能是因为他们太忙而无法填写，或者是因为他们没有正确理解，无法正确填写。例如，故障描述中仅列出一个发动机故障。可靠性工程师很难理解这一描述，更不用说事后分析了。记录不正确。第二，数据信息不对称。航空公司可以通过多种方式检测航班错误和系统故障。同时，还存在信息不对称的问题。调查结果可能不同于多个系统。在这个系统中可能会发现一些错误，但在其他系统中找不到或以不同的方式表示。这使可靠性工程师能够在研究过程中比较不同的系统，从而增加不必要的时间损失。建议使用具有相同错误内容的单个数据源。来自同一表格的信息可以减少填表人之间的差异。如果问题的两种描述不同，可靠性工程师可能无法确定哪一种具有优先。
二、飞机可靠性分配分析
可靠性分配是将系统或产品的子系统、设备和组件的可指标分配到所有功能级别，以确定每个子产品的可靠性指标。飞机系统可靠性设计是一个非常复杂的过程，包括工程系统的选择、简化和各种冗余系统的使用。不同的系统架构取决于它们的重要性、复杂性、影响和成熟度。根据确定的可靠性要求，评估所需的管理信息，如人力需求和人力资源。飞机系统可靠性分配方法主要包括有等分、评分、比例组合、考虑重要度和复杂度的分配法等，如果等分配法产品定义不明确，则简单分配方法采用。在没有产品可靠性数据的情况下，可以使用评分分配法，但由经验丰富的工程师和评估技术人员给出，这是非常主观的。如果新系统与旧系统相似，则可以根据新的需求按比例分配新系统。在详细规划中，通常采用重要度和复杂度相结合的分配方法。该方法考虑了系统或设备的重要性、复杂性和持续时间，能够更好地满足可靠性指标分配的要求。然而，在工程实践中，每个系统的值往往是由人来确定的，或者为了简化计算，通常假设每个系统的值是相同的值，导致可靠性指标分布存在一定的偏差。针对上述情况，将灰色关联理论应用于可靠性分配方法中，解决了数据量小、主观影响大。
三、方法的提出与模型的建立
1.考虑分配方法的重要和复杂性。该分配方法考虑了重要性和复杂性。可靠性指标表示为TBF和I子系统基于故障间隔的可靠性指标：
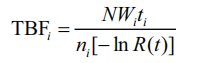(1)
式中：i子系统编号(I=1.2.3、…、I)；ti子系统正常运行时间，Wi子系统故障和严重系统故障；ni子系统中组件的数量N，
；R(t)系统组件的数量表示系统的可靠性。事实上，由于缺乏简化的支持方法和数据，Wi管理通常假定每个飞行系统的值相同。显然，这不是正确的做法。例如，飞机动力装置和控制直接与安全影响。故障可能导致明显比其他系统更重要的损坏和人身伤害。
2.根据灰色关联理论重要度因子计算。灰色关联理论是根据各个因素的不同趋势将不同因素联系起来的一种方法，灰色关联理论是一种数值检索方法，即当认识到连续序列之间的密切关系时，形成过程可创建参照曲线和相关曲线，并用类似形式的基准曲线直观地强调相互连接的曲线之间的密切关系。曲线越接近灰色理论。关系越密切，联系就越多。相反，约束越少。灰色关联分析的计算步骤如下:原始序列的定义。控制顺序必须为0x 0(k)，以表示每个可比系统所需的可靠性指标。其他列表示系统i个的k子系统的可靠性指标，类似于相应列被记录为Xi(K)。)对数列作无量化，将数值序列转换为无单位的相对值
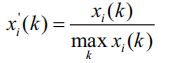(2)
根据变换的资料，计算在不同关联数列为指定的关联系数ξi(k)，公式计算如下:
（3）
σ是解析系数，通常接受[0.1]范围内的值。相关性。该计算基于不同时间点的相关系数平均值，计算方法如下。
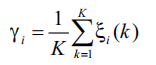(4)
其中k是相似系统的数量，关联数列γi，Xi与原始序列x 0之间的灰色关联。飞机制造商提供的可靠性数据足够。按照一些程序，它反映了飞行性质的重要性。初始曲线基于整个单元的可靠性指标，与子系统的可靠性指标相对应。如果相应的子系统曲线接近整个飞机的相应曲线，则认为子系统至少如此重要。因此，wi因子值可以是灰色关联度γi系统。
四、飞机系统可靠性分配
某型飞机由机体结构、动力系统、供油、环控、液压、自动化、消防、氧气、电气、辅助、导航和指示记录系统组成。
1.载机可靠性模型。载机可靠性模型采用考虑到计算复杂性和飞行现实的串联模型。
2.以用于执行可靠性分配任务的飞机为基础；每个载机系统的寿命指数分布。无故障飞机(MFHBF)的平均运行时间不应小于8.5小时，运行可靠性不应小于0.9小时。为了减少分配过程中可靠性分布的重复次数，必须满足一定数量的要求。根据其他模型的经验和其他中国模型的最佳做法，在改变技术状况时考虑到剩馀的20%。因此，8.5h的目标值(MFHBF)必须转换为定义的MTBF目标值，MTBF的可靠性分布值为10.2h。任务可靠性也是最后期限目标的20%，因此任务可靠性估计为0.916%。公式(1)表示系统的复杂性主要取决于系统组件的数量。系统组件越重要，系统就越复杂。由于技术成熟xi进行统计。如表1所示计算出重要和改进部件的数量。机体15，动力96，燃油78，环控48，液压30，自控102，操纵36，座椅及生活设备7，防火10，氧气24，电气76，救生2，座舱87，通信47，导航102，指示记录75，总计部件总数为835。系统如表1所示MFHBF值。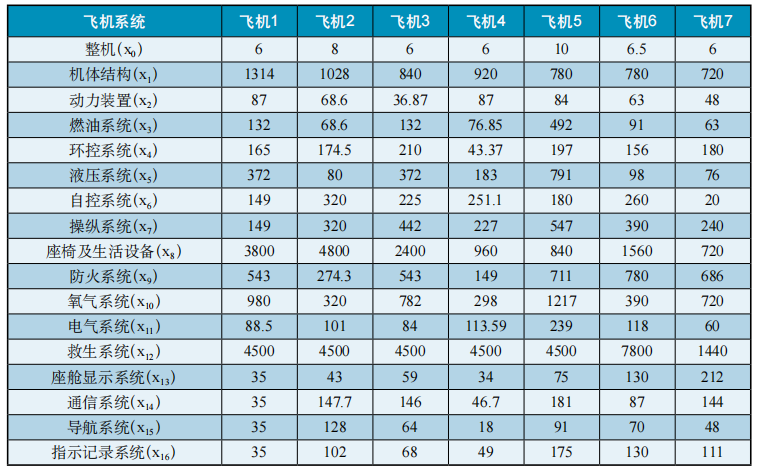
表1各型飞机系统MFHBF值（单位：h）
可以通过用公式（3）（4）代入表1中的数据来计算每个系统的值。计算ρ取0.5的公式（3）中。计算每个系统的值后，可以使用公式（1）代入每个系统的分配结果，并四舍五入到最接近的整数。
3.结论分析。与比例组合相比，飞机结构、座椅设备、氧气和救生系统的平均无故障时间更长，这降低了其他系统的可靠性，对飞行安全或任务性能没有显著影响。在这种方法中，这些系统与其他系统一样重要。因此，将这些系统的可靠性指标分解为其他系统，以补偿航空系统的可靠性。对于新改进的成品系统，如自动控制系统，通常需要降低可靠性指标。然而，文本分配结果高于比例组合，这有助于成品制造商提高设计过程水平并提供更大的可靠性。
考虑到飞机系统的重要性、复杂性，本文将灰色关联理论应用于可靠性分配方法。实例表明，该方法在一定程度上解决了数据量小、主观影响可靠性分配结果的问题，提高了可靠性分配计算的合理性。该方法简单可行，但同时存在两个问题：国内飞机可靠性研究起步较晚，灰色关联数据相对较少，无法清晰了解系统数据曲线。随着时间的推移，积累的数据越来越多，意义的计算也越来越准确。技术成熟度只反映在新的和改进的最终产品的数量上。这些产品不能充分反映实际工程技术环境，需要进一步研究和解决。
参考文献：
[1] 商成.一种新的飞机系统可靠性分配方法[J].兵工自动化，2020，19(12)：16-19.
[2] 尤维.一种面向设计寿命全过程的电子系统可靠性分配法[J].电子产品可靠性与环境试验，2019，30(1)：32-36.
[3] 张敏婷.航空发动机可靠性评分分配法[J].质量与可靠性，2019，140(2)：49-53.
[4] 曾华.任务可靠性指标分配的比例组合法及评分分配法[J].航空学报，2020，16(8)：15-20.
[5] 李必.飞机设计手册编委会.飞机设计手册（第20册）[M].北京：航空工业出版社，2020：85-91.