1 引言
目前常用的城市架空输电线风致响应振动技术主要包括风洞试验、路风分析、有限元分析等。其中风洞试验是评估电力架空输电线与地面风荷载及道路振动响应之间是否存在关联的重要方法之一。本文将结合路风电场数据和实际情况，制定符合城市电力系统振动控制技术规范要求的路风响应模型以及建模方法。该模型包括风载和风力载荷及其波形结构参数（如频率因子)，并根据实际情况在路缘设置了固定标度因子（风速）及路载波频率等参数，以此更好地分析架空输电线路风致响应振动情况。
2 结构动力特性分析
2.1 输电杆塔
由于外部载荷对其自振性能的影响较小，且其频率近似于独立的数值，因此在计算输电杆塔的动态性能时，可以忽略外部载荷的影响。无导线传输杆塔各向三阶自振频率。结果显示，在两个垂直的平面上，除扭转方向以外，其各个阶次的频率相近，这是因为主塔主结构呈对称方型，刚度分布均匀，而不同点是因为导线在纵向上的水平分布不均匀。而且，随振型阶次的增大，各个方向的频率都会增大，而且在同一阶各个方向上的频率会彼此相近，这是因为在高频模式下，各向振动耦合能力会加强，模态阶愈高，这一特性就愈显著。
2.2 输电电缆
在不考虑输电杆塔的情况下，将输电杆塔的刚度调整到远大于输电线路刚度的情况下，对平均风速下的地线动态性能进行分析，得出地线的各个阶次比导线稍高的原因，这是因为其单元长度比地线大，存在着质量衰减的效果；在静载荷作用下，导地线的各个阶次频率都比前者稍高，这表明静载荷作用能明显增加导线的初始预拉应力，使导线的拉力刚化效应得以显现，并以频率的细微提高为特征。分析结果还发现，架空高程对其自振频率的影响不大。
2.3 架空输电线路
架空输电线路的振动特征从传输线至输电杆塔呈现出由高到低的特点，这主要是因为导线与导线的刚性不同，导线的刚性较低，从而使导线的频率较低。而输电杆塔由于其刚性较大，其频率也相对较高，因而难以在一定的模式下充分体现其基本频率。对于电线，线路与输电线路的耦合会使线路的振动降低；输电铁塔，导线、绝缘子等与输电铁塔之间的耦合也具有质量阻尼作用。
3 动力响应分析
在时间域上对架空输电线路的动态反应进行研究，即计算了在静载荷和动态载荷下的塔尖位移、基底主柱应力、传输线轴力的最大概率，以下将对其进行分析：
3.1 基于三点轴位移分析法建立风致响应模型
本文采用 Field Mode进行数值计算结果分析，其计算结果的离散形式呈现，随着风速的增大，大气动力学与大气运动耦合作用不断增强，速度与加速度之比呈现先增大后减小、先线性后非线性的变化趋势。当风速增大至10 m/s时，大气动力学与大气运动耦合作用趋于消失。而当风速增大至15 m/s时，大气动力学振动响应强度增大，且具有明显的频率差的特征。因此，本文采用三点轴位移分析法建立气动力仿真模型，并模拟大气动力学与大气运动耦合作用等。
3.2 频率因子法
对于输电线而言，风的激振力主要是由频率因子所决定的。通常来说，频率因子在0至90 kHz范围内，具有明显的方向性，风速为1.5 mpa，故0至90 kHz的范围内风速的变化较小；而当风速为2.0 mpa时，且0至90 kHz范围内均有显著的风载荷产生。同时，风速减小时产生振动的频率越低，即越容易识别出风速降低方向、风速增大引起振动发生时的风载荷变化规律。因此，若要得到精确的风致响应曲线，将需要准确识别出风速降低方向、风速增大引起的风流载荷变化规律。
3.3 耦合振型解析分析
当最大风速达到10.5 m/s时，风场中出现一个峰值，并且其与水平风压源耦合产生了一个正反馈，而后开始削减。同时，对于同一条路不同风压源时，各个耦合振型的最大频率为15.1 Hz，但该耦合振型与水平风压源耦合振型的最大加速度值相差不大。
3.4 风致响应计算方法及风场仿真
本文所采用的风场计算方法是将风速与风力分布函数相加，得到风速下导线对风的响应矩阵，其中矩形表示导线和风阻所引起的风速变化量。根据空气动力学理论，可以得到导线两侧不同长度的电场强度、风加速度、风场辐射速率等相关参数，其结果可为数值计算提供一定的理论依据。
在 MATLAB中建立模拟模型，设置风致振动频率为0.09 Hz。该模型建立了风道、风体等多个模型，在最大风场出现后，输电线路在风致振动响应下出现一定频率的振动，在最小风量出现后频率趋于平稳。从最大风量与频率关系图可见，线路最大最小振幅分别为0.09 Hz (−20 dB)、−40 dB (−10 dB)、−35 dB (35 m/s)和−30 dB (35 m/s)。其中，在最大风量出现后，每增加一个档位后，电缆路振幅减小一个单位，即此时每一档位处电缆路的振幅减小了一个单位。对于连续风速较大的情况，需加强对线路运行参数的控制，以保证线路运行正常可靠。架空输电线路风致响应振动位移最大值的概率密度函数可表示为如下形式：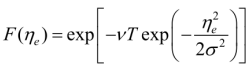
式中：ηe为位移响应量；ν为有效零穿越频率；T为持续时间；σ为位移标准差；0.5772γ=为欧拉常数。
采用公式并忽略微小的横风向响应分量，可确定输电杆塔顶端位移脉动分量的标准差和极值。
期间根据空气动力学理论，可以得到导线两侧不同长度的电场强度、风加速度、风场辐射速率等相关参数，其结果可为数值计算提供一定的理论依据。为了便于风场仿真分析，本文将风场建模与测试工作同步进行。首先对线路进行几何简化，建立风场模型，然后再用风致振动响应分析软件 Tremek对不同速度、不同风速下导线对线路风场响应矩阵进行分析，得到导线振动范围和幅值分布曲线和响应时间等与计算结果相对应的特性参数。其中方程组为求解方程时采用经典模型法求解；风加速度作为参数法可用于建立风致振动响应矩阵；幅值曲线和风速曲线如图1所示。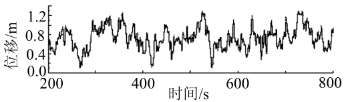
图1 风湍流作用
通过风场仿真计算模型得到输电线路在不同风速条件下气流结构及空气动力学特性，以及各风点与路径的电场强度分布，进而分析该段线路风致振动影响特征。
结束语
本文通过对风荷载和路风响应进行计算分析，得到以下结论：（1）通过路风模型计算了架空输电线在不同风速下的路风响应，路风响应主要受风速、空气流动以及风对线路的影响。（2）当风速超过6 m/s时会出现路风响应急剧增强现象，而风速越大、发生时间越短、发生频率越高。由于受大气运动及路面的变形影响，风荷载主要集中在结构表面、线段内部以及两侧空气层之间；但在实际路风载荷作用下其分布情况与空气流速、方向及风向等因素有关；当风速较小或呈水平时，其振动强度较小。（3）结构体系的动态响应是由低阶模态贡献引起的，而在此基础上，其所起的作用是绝对的。因此，在采用频率域简化的方法进行结构设计和分析时，采用前几阶模态反应的联合计算，其结果是完全符合实际工程要求的。
参考文献
[1]刘春城,孙红运.山脉地形迎风面输电线路风偏响应特性[J].振动工程学报,2022,35(04):1020-1028.
[2]吴田,张超,方春华,黎鹏,普子恒.特高压输电线路塔线体系风振响应特性及对登塔人员影响分析[J/OL].高压电器:1-11.
[3]杨继业,李健,马强,陈曦,刘涛,毕岩,李秋澎,刘雨菲.输电线路非线性脱冰耦合振动数学模型及振动响应参数优化[J].工业建筑,2019,49(12):13-18.