I. 介绍
随着社会经济的快速发展，电力负荷峰谷差逐年增大，电力系统供需平衡问题日益突出[1]。此外，随着 "双碳 "和 "构建以新能源为主体的新型电力系统 "目标的提出[2, 3]，可再生能源发电将大规模渗入电网，其随机性和波动性对电网运行是一个很大的挑战[4]。储能为解决上述问题提供了重要而有效的途径，是未来以高比例可再生能源为主体的电网和能源系统的重要组成部分和关键支撑技术。
为了保证电网供需平衡，促进可再生能源消纳，促进电网安全稳定运行，不采取一定的调峰措施是不行的[5]。传统的方法是增加调峰电源的建设容量，以满足负荷高峰和低谷阶段的电力需求[6]。这种方法会导致 1）调峰机组容量建设成本增加[7]；2）设备利用效率降低[8]；3）机组频繁启停导致成本损失增加[9]。随着技术的成熟和成本的逐年降低，在电网侧建设大型储能站，实现电力系统的移峰填谷已具备现实条件[10]。储能具有吞吐量快的特点，可实现负荷功率在时间轴上的平移，从而减少系统负荷的峰谷差[11，12]。
近年来，学者们对储能在电力系统调峰中的应用进行了广泛的探讨和研究。文献[13]提出了储能系统的恒功率调峰填谷优化模型和求解该模型的实用简化算法。以中国南方电网兆瓦级储能示范工程为背景，验证了算法的有效性。文献[14]提出了一种变功率控制策略，其中储能参与配电网的负荷移峰填谷。以储能系统的功率平衡为标准，有效改善配电网的峰谷差。一些研究考虑了可再生能源并网引起的消纳问题。例如，文献[15]在考虑系统经济性和风电消纳及调度原则的基础上，提出了含储能电站的移峰填谷优化调度方法。文献[16]验证了商业园区储能削峰填谷的可行性，提出了储能系统削峰填谷的变参数功率差控制策略，并验证了所提策略的有效性。然而，上述研究都没有充分考虑储能本身的容量约束、功率约束、充电状态约束、放电深度约束和爬坡约束，以及储能配置的容量功率比对调峰填谷控制策略的影响。
鉴于此，本文综合考虑了储能系统的各种约束条件，提出了储能参与电力系统削峰填谷的恒功率控制策略和变功率控制策略。首先，从角度建立了考虑多因素的储能一般模型，从电网角度建立了负荷峰谷特性评价指标。然后，建立了考虑储能约束条件的恒功率控制策略和变功率控制策略的求解模型。最后，以海南文昌北部区域电网为例，模拟比较了两种控制策略的优缺点和储能容量功率比的适用性。
II. 储能参与削峰填谷
储能系统参与电网的移峰填谷是利用储能的快速吞吐特性，将电能从低负荷阶段转移到高峰负荷阶段，从而实现系统负荷的移峰填谷。对于储能，应充分考虑储能的约束条件，即在储能的约束条件下，充分利用储能的潜力，实现负荷的移峰填谷。对于电网而言，有必要建立一个量化指标来衡量储能在移峰填谷后的负荷效应。
A. 储能模型
储能模型描述了剩余电量、充电状态、放电深度、充放电功率、充放电效率、离散时间尺度等参数之间的关系，指出了储能参数的时间耦合关系和放电深度极限，是研究储能在电力系统削峰填谷控制策略的基础。
1) 剩余电量
在实际工作中，储能的剩余电量是一个连续变化的过程。为了便于计算，本文将储能工作过程离散化为 N 个时间段，相邻时间段的储能剩余电量更新公式为：
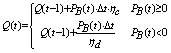(1)
其中，
为 时间段内的剩余电量；
为时间段内的充放电功率，大于 0 表示充电，小于 0 表示放电；
为离散时间尺度；
和
分别为充电效率和放电效率。由此可见，剩余电量之间存在着严格的时序耦合关系。当前时刻剩余电量的大小决定了其参与移峰填谷的能力，并影响储能后的作用。
2) SOC
充电状态（SOC）是储能运行中的一个重要参数，它被定义为剩余电量与总储能容量之比。
(2)
其中，
为时间段的充电状态；
为储能的额定容量。与剩余电量类似，充电状态也有如下更新关系：
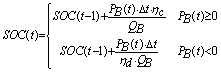(3)
3) 放电深度（DOD）
放电深度（DOD）是衡量储能是否健康的另一个重要参数。它被定义为储能释放的能量与储能总容量之比。
(4)
储能的放电深度必须严格控制，一旦深度放电将严重影响储能的使用寿命。因此，在储能的运行过程中应增加硬性约束，避免发生深度放电。
储能参数具有复杂的时间序列耦合关系，这导致储能模型充放电策略的管理不能从单一时间段考虑，而必须考虑一天 24 小时规模的输出策略，以达到最佳的移峰填谷效果。
B. 负荷峰谷特性评价指标
峰谷填充效应的评价指标包括峰谷差绝对值、峰谷系数、局部响应载荷的峰谷差率和整体响应载荷的载荷波动标准偏差。
1) 绝对峰谷差
(5)
其中，
代表最大负荷；
代表最小等效负荷。负荷的绝对峰谷差代表一定时间尺度内负荷的最大绝对偏差。指数越小，负荷峰谷差越小。
2) 峰谷系数
(6)
负载的峰谷系数表示负载在一定时间范围内的波动程度。峰谷系数越大，负载峰值和谷值之间的差值就越小。
3) 峰谷差
(7)
峰谷差表示一定时间范围内的负荷波动程度。峰谷差越小，负载波动越小。
4) 负荷波动标准偏差
(8)
负荷波动的标准偏差代表总体负荷波动。负荷波动标准差越小，总体负荷越平缓。
III. 储能的峰谷填充控制策略
A. 恒功率充放电控制策略
恒功率充放电策略是指储能系统以恒定功率参与充放电，不考虑储能的爬坡约束。通过控制储能在每个时段的充放电状态，改变系统的峰值负荷，达到填谷的目的。1) 储能必须满足充放电状态的约束。只有充电、放电和恒功率浮充三种状态。2) 相邻时段充放电状态的约束；3) 充电状态约束；4) 能量约束。
1) 目标函数
为了达到最佳的移峰填谷效果，以负荷曲线方差最小为目标函数。负荷方差越小，负荷峰谷差越小，整体负荷波动越小，移峰填谷效果越好。目标函数的设定不仅能减小系统负荷的峰谷差，还能实现整体负荷曲线的平滑。
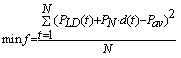(9)
(10)
其中，
代表实际负荷；
代表储能的额定功率；
代表平均负荷；
代表离散化后的时间段总数；
代表 T 期间储能系统的充放电状态。
2) 制约因素
a) 充放电状态限制
(11)
储能只有三种恒功率充放电状态：充电、放电和浮充。
b) 对相邻时段充放电状态的限制
(12)
这种约束保证了储能不会直接从满电过渡到满充，或从满充过渡到满电，保证了储能的健康运行状态，有利于寿命的提高。
c) 充电状态限制
(13)
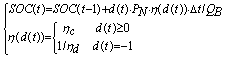(14)
其中，
是充电状态的下限；
是 soc 状态的上限。这一约束条件可确保储能在运行期间处于良好的充电状态，否则将损害寿命。
d) 电量限制
(15)
储能在最后运行时段的 soc 值必须大于开始运行时段的 soc 值，这样才能确保储能在第二天参与电网运行。
储能参与负荷调峰的恒功率控制策略的求解变成了确定储能在每个时段的充放电状态，以达到最小负荷方差的目的，这是一个带整数变量的二次型编程问题（QP）。对于二次型编程问题的求解，如拉格朗日法、莱姆克法、内点法、有效集法、椭圆算法等，也可以直接使用求解器求解 QP 问题，借助求解器资源，一般 QP 问题都能成功求解。下面是通过基于 MATLAB 平台的 YALMIP 工具箱调用 GUROBI 求解器求解问题的流程图：
图1.恒功率充放电控制策略流程图
该策略计算简单，易于在工程实践中应用。控制策略制定快捷方便。储能系统以恒定功率充放电，只需确定储能系统在每个时间段的充放电状态。
3) 改进的恒功率充放电策略
根据上述模型可以看出，恒功率充放电策略有一个很大的缺陷，即该策略对储能容量功率比的适应性较差。一旦储能的容量功率比很小，恒功率充放电策略就无法发挥移峰填谷的作用。因此，上述模型需要改进，即不要求储能以额定功率充放电，而是设定合理的充放电功率。
(16)
(17)
其中，
为改进后的储能充放电功率；
为常数，与储能连续响应时间、效率和初始荷电状态有关；
为储能连续响应时间，一般取 2 小时；
为储能初始荷电状态，一般取 0.2。
B. 变功率充放电控制策略
考虑到恒功率充放电控制策略对储能容量功率比的适应性较差，储能功率对负载曲线的跟踪能力稍差，这里提出一种变功率控制策略，既能适应不同的容量功率比，又能达到最佳的移峰填谷效果。
1) 目标函数
变功率控制策略的目标函数也被定义为最小负荷方差，它可以协调一天周期内不同时段的储能充放电功率，实现最佳的峰谷负荷跟踪。
(18)
其中，
为储能的充放电功率，充电为正，放电为负。
2) 制约因素
a) 功率限制
(19)
其中，
为储能的最大放电功率；
为储能的最大充电功率。
b) 充电状态限制
(20)
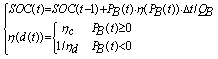(21)
c) 爬坡限制
(22)
其中，
是攀升的百分比。
d) 能量限制
(23)
建立的模型是二次编程（QP）问题，也是通过使用 MATLAB 的 YALMIP 工具箱调用 Gurobi 求解器求解的。其控制策略流程图与图 1 类似。区别仅在于目标函数和约束条件的不同，不再赘述。
与恒功率充放电策略相比，变功率充放电策略的优势在于储能可以灵活调节输出，更好地满足负载需求，从而达到最佳的移峰填谷效果。同时，变功率控制策略对电力电子变流器及其控制系统的要求较高，需要实时控制储能的输出。
IV. 模拟结果
以海南省文昌市北部地方电网为移峰填谷场景。下图为该地区典型的日负荷曲线（基本负荷叠加小规模分布式可再生能源发电）。
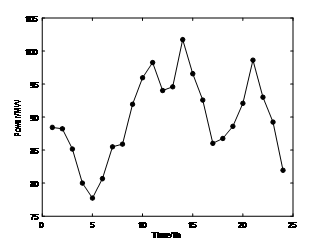
图2. 基础负荷数据
文昌北部地区日总负荷峰谷差明显：最大负荷 101.74MW，最小负荷 77.74MW，峰谷差 24.00MW，峰谷系数 0.76，峰谷差率 0.24。负荷波动标准差为 6.18MW，负荷总体波动范围较大。
计算示例设置了不同的储能容量功率比，以探讨不同控制策略下的移峰填谷效果和适应程度。
1) 储能容量功率比
设定储能系统的额定容量为 12MWh，额定功率为 5MW，充放电效率为 0.9，储能系统的初始充电状态为 0.2。
基于图 2 的负载曲线，验证恒功率充放电策略和变功率充放电策略的削峰填谷效果，图 3 和图 4 是恒功率充放电策略下优化前后与储能系统的负载曲线对比，图 5 和图 6 的输出分别是变功率充放电策略下优化前后的负载曲线对比与储能系统输出功率。
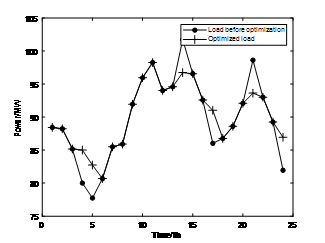
图3. 恒功率充放电策略下优化前后的负载曲线对比
图4. 恒功率充放电策略下的储能输出功率
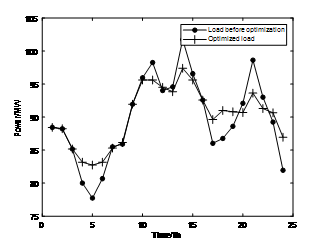
图5. 变功率充放电策略下优化前后的负载曲线对比
图6. 可变功率充放电策略下的储能输出功率
从上图可以看出，当容量功率比为 2.4:1 时，两种控制策略都能达到移峰填谷的效果，且变功率控制策略的移峰填谷效果优于恒功率控制策略。两种控制策略的移峰填谷指标如表 1 所示。
表1. 负荷峰值移动和填谷效应指数对比（
）
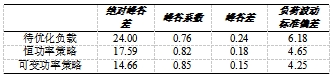
可以看出，在此容量功率比（
）下，两种策略都能改善负荷的峰谷特性指标，但变功率充放电策略的移峰填谷效果指标优于恒功率充放电策略。这是因为在变功率策略的指导下，储能系统更加灵活，可以灵活跟踪负荷的变化。相反，在恒功率策略的指导下，储能系统只能以恒定的功率充放电，不能更好地匹配峰值负荷充放电需求。
2) 储能容量功率比 
储能系统的额定容量设定为 12MWh，额定功率设定为 8MW，充放电效率设定为 0.9，储能系统的初始充电状态设定为 0.2。
模拟结果如下： 图 7 和图 8 分别为恒功率充放电策略下优化前后的负载曲线对比和储能系统输出；图 9 和图 10 分别为变功率充放电策略下优化前后的负载曲线对比和储能系统输出功率。
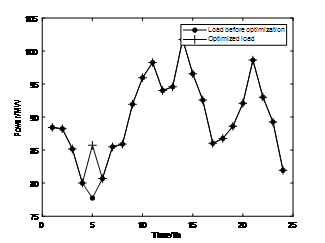
图7. 恒功率充放电策略下优化前后的负载曲线对比
图8. 恒功率充放电策略下的储能输出功率
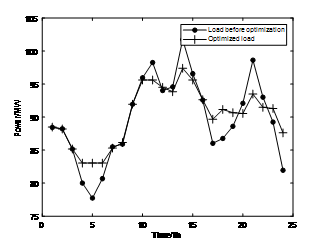
图9. 变功率充放电策略下优化前后的负载曲线对比
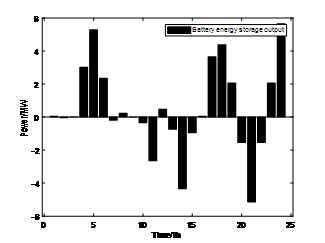
图10. 可变功率充放电策略下的储能输出功率
从上图可以直观地看出，在此容量功率比下，恒功率充放电策略无法起到移峰填谷的作用，而变功率充放电策略则可以。
当 m=3 时，恒功率充放电策略将得到进一步改进。图 11 和图 12 分别显示了改进后的恒功率充放电策略下优化前后的负载曲线对比和储能系统输出。
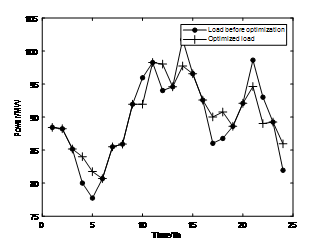
图11. 在改进的恒功率充放电策略下，优化前后的负载曲线对比
图12.恒功率充放电策略下的改进型储能输出
两种控制策略的移峰填谷指数见表 2。
表2. 负荷峰值移动和填谷效应指数对比（
）
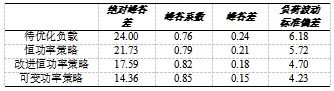
从上表可以看出，当储能系统的容量功率比为 3:2 时，变功率控制策略的移峰填谷效果更为显著：优化后，变功率控制策略下的绝对峰谷差为 14.36MW，恒功率控制策略下的绝对峰谷差为 21.73MW。整体而言，变功率控制策略下的负荷波动标准差为 4.23，恒功率控制策略下的负荷波动标准差为 5.72。
但恒功率充放电策略改进后，移峰填谷效果指标提高，负荷绝对峰谷差为 17.59MW，负荷波动标准差为 4.70。但与变功率控制策略相比，效果还是稍差一些，因为储能系统的电能并不能在每个时段都得到合理利用，存在电能浪费或过度使用的现象。
V. 结论
本文在分析储能模型和移峰填谷评价指标的基础上，综合考虑储能自身的各种约束条件，提出了储能参与电力系统移峰填谷的恒功率控制策略和变功率控制策略。结论如下：
1）在不同储能容量功率比情况下，变功率控制策略比恒功率充放电策略具有更显著的移峰填谷效果。变功率控制策略的充放电形式更灵活，对储能容量和功率比的适应性更强，能更好地跟踪负荷移峰填谷的要求。
2) 改进后的恒功率充放电策略可以发挥移峰填谷的效果，改进方法具有实际工程意义。
参考文献
[1] 董慧峰,李文启,牛文迪,等. 储能系统参与电网削峰填谷实用算法[J]. 电测与仪表,2019, 56(18): 74-78.
[2] 韩肖清,李廷钧,张东霞,等. 双碳目标下的新型电力系统规划新问题及关键技术[J]. 高电压技术,2021,47(09):3036-3046.
[3] 赵剑波,王蕾. “十四五”构建以新能源为主体的新型电力系统[J]. 中国能源,2021,43(05):17-21.
[4] 郭敏晓,杨宏伟. 围绕“碳中和”愿景 能源与环境领域将呈现六方面的变化趋势 “十三五”能源与环境形势及“十四五”展望[J]. 中国能源,2021,43(03):19-23+58.
[5] 赵书强,吴杨,李志伟,等. 考虑风光出力不确定性的电力系统调峰能力及经济性分析[J].电网技术,2022,46(05):1752-1761.
[6] 崔杨,周慧娟,仲悟之,等. 考虑火电调峰主动性与需求响应的含储能电力系统优化调度[J]. 高电压技术, 2021, 47(05): 1674-1684.
[7] 杨寅平,曾沅,秦超,等. 面向深度调峰的火电机组灵活性改造规划模型[J]. 电力系统自动化,2021,45(17):79-88.
[8] 卓振宇,张宁,谢小荣,等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化,2021, 45(09): 171-191.
[9] 陈晓利,高继录,郑飞,等. 多种深度调峰模式对火电机组性能影响分析 [J].热能动力工程,2020, 35(12): 26-30.
[10] 宋安琪,刘成. 分布式储能参与广东电力市场的规则研究[J]. 机电信息,2019,(32):121-123.
[11] 郭莉,薛贵元,吴晨,等. 储能系统应用于削峰填谷的经济效益分析研究[J]. 电力需求侧管理,2019, 21(05): 31-34.
[12] CHEN Y T, WANG X L, WANG J X, et al. Power Control Strategy of Battery Energy Storage System Participating in Power System Peak Load Shifting [C]. 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE).2020:710-715.
[13] 陈满,陆志刚,刘怡,等. 储能系统恒功率削峰填谷优化策略研究[J]. 电网技术,2012, 36(09): 232-237.
[14] 孟娅,李欣然,黎淑娟,等. 储能参与配电网削峰填谷的变功率控制策略[J]. 电力建设, 2018, 39(04): 45-50.
[15] 林俐,费宏运. 规模化分布式光伏并网条件下储能电站削峰填谷的优化调度方法[J]. 现代电力,2019, 36(05): 54-61.
[16] 杨锡运,董德华,李相俊,等. 商业园区储能系统削峰填谷的有功功率协调控制策略[J]. 电网技术, 2018, 42(08): 2551-61.