一、引言
流体力学的计算是研究流体力学数值模拟方法的一门基础学科。随着电子计算机技术的飞速发展,流体力学这一学科越来越受到人们的重视[1]。目前计算流体力学通常为有限单元法、有限差分法、有限体积法等。要深入理解并掌握计算流体力学就要从基础的流体力学理论入手。
二、流体力学基础知识
2.1控制方程
控制所有流体流动的三个基本定律为:质量守恒定律、动量守恒定律和能量守恒定律,由它们可以分别计算和推导得出流场的质量守恒方程、动量守恒方程和能量守恒方程,因此称其为控制方程。
(1)质量守恒方程
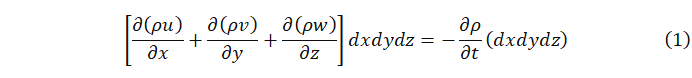
或可写成:
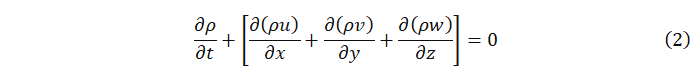
表达式中的![]() 部分代表时间内通过单位面积的流体质量,改写成矢量形式可表示为:
部分代表时间内通过单位面积的流体质量,改写成矢量形式可表示为:
![]()
(2)动量守恒方程
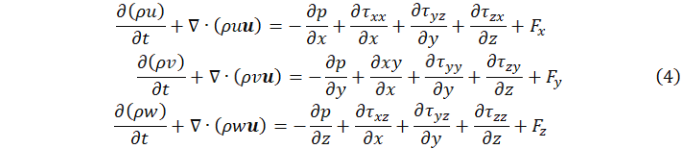
式4中,p为流体中微元中静压 ;![]() 为微元体表面上的粘性应力在各个方向上的分量;微元上的体积力为
为微元体表面上的粘性应力在各个方向上的分量;微元上的体积力为![]() ,当微元只受重力且延Z轴竖直向上时,对于牛顿流体可引入粘性切应力公式:
,当微元只受重力且延Z轴竖直向上时,对于牛顿流体可引入粘性切应力公式:
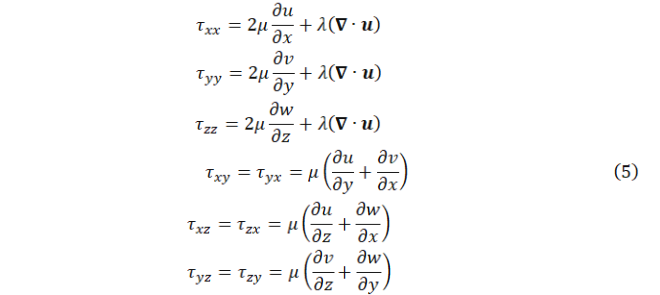
式5中μ为分子粘性系数,λ为第二粘性系数,根据Stokes假设知:
![]()
将公式整理可得到动量守恒方程:
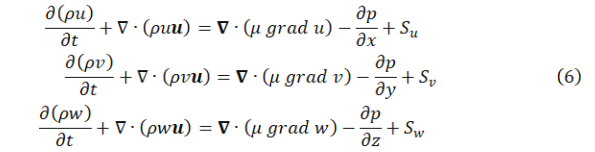
式6中![]() 为动量守恒方程的广义源项,
为动量守恒方程的广义源项,
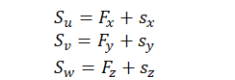
将![]() 三项展开得到:
三项展开得到:
![]()
![]()
![]()
式7中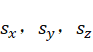 都是很小的量,对于不可压缩流体而言分子粘性系数μ和第二粘性系数λ为常数。
都是很小的量,对于不可压缩流体而言分子粘性系数μ和第二粘性系数λ为常数。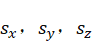 三项均为0。
三项均为0。
(3)能量守恒方程
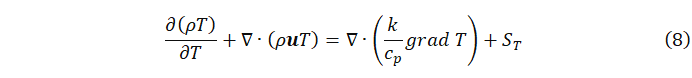
将上式展开可得:

式9中cp为比热容,T为温度,k为流体的传热系数,ST为流体的粘性耗散项。
2.2 纳维-斯托克斯方程方程
纳维-斯托克斯方程(Navier-Stokes equations),简称N-S方程,是用来描述粘性不可压缩流体动量守恒的运动方程。
它的矢量形式为:
![]()
在直角坐标中,可写成:

式中,![]() 是流体密度;P是压力;V是速度矢量,
是流体密度;P是压力;V是速度矢量,![]() 是流体在t时刻,在点
是流体在t时刻,在点![]() 处的速度分量;f是单位体积流体受的外力,若只考虑重力f=pg则;常数μ是动力粘度。
处的速度分量;f是单位体积流体受的外力,若只考虑重力f=pg则;常数μ是动力粘度。
由于N-S方程反映了粘性不可压缩流体及其流动的基本力学规律,所以其在流体力学中具有十分重要的地位和意义。
2.3 雷诺平均N-S方程
雷诺平均方程是一种用来描述湍流统计量的演化的系综平均N-S方程。若从N-S方程出发对湍流进行直接数值模拟(DNS),将难以解决工程中会遇到的实际的复杂湍流问题,在这种复杂的情形下,求解雷诺平均的N-S方程(RANS)方法成为了当前在解决工程实际问题中较为有效的一种手段。
雷诺平均N-S方程实际上是对流场平均变量的一种控制方程,与其相关的湍流模拟理论被称之为湍流模式理论。雷诺平均湍流控制模式方程的理论首先假定一个湍流运动过程中的每一个流场平均变量由一个湍流的时均量和一个脉动量组成,由此便可以直接得出雷诺平均N-S方程。
连续方程:
![]()
动量方程:
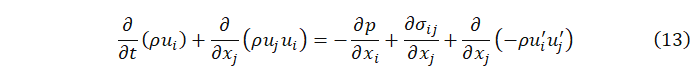
式12和式13中ui表示略去平均符号的雷诺平均速度分量,![]() 为密度,p为压强,
为密度,p为压强,![]() 为脉动速度,
为脉动速度,![]() 为应力张量分量。
为应力张量分量。
三、计算流体力学基础
3.1 计算流体力学原理
计算流体力学(Computational Fluid Dynamics)是20世纪60年代开始随着计算科学与工程迅速发展起来的一门综合性学科的分支,在经过半个世纪多的研究以及高速发展之后,已经发展为相当成熟的一门学科。其主要的研究方法是通过计算机运算和数值模拟的方法来求解传统的流体力学的控制方程,对流体力学的相关问题进行模拟和分析。
CFD的计算方法是将流场的控制方程运用计算机计算的方法将其离散到一系列网格节点上求其数值解。由基本原理出发,可以建立质量守恒方程组、动量守恒方程组、能量守恒方程组、湍流特性等。这些方程构成的非线性偏微分方程组不能用经典的解析法来求解且只能通过数值计算的方法求解。在进行求解计算时,应当要确定计算模型的尺寸形状和计算域的边界条件,例如,进出口压力、进出口温度、工质条件、固壁边界和湍流模型。
3.2 数值模拟方法
在运用CFD方法对一些实际的问题进行模拟时,算法的选择对于模拟的效率及计算的正确性都具有很大的直接影响。区域离散化的方法是使用有限个离散的点来代替原有的连续空间,过程中把计算域分为许多互不重叠的子域,确定每个子域节点的位置和代表的控制体的体积。较为常用的离散化计算方法包括有限差分法、有限单元法和有限体积法三种。
(1)有限差分法
有限差分法是数值求解方法中的经典方法。其原理是先将计算域划分成一组差分网格,再用离散网格来代替连续的计算域,然后将偏离散点的控制方程的导数用差商来代替,由此推导得出一个含有离散网格节点上有限个未知数的有限差分方程组。
(2)有限单元法
有限单元法的基本思想是先将计算域划分为有限个互不重叠的微小单元,并在每个单元内选择一些作为求解函数的插值点的节点,再将微分方程中的变量改写成由插值函数所组成的线性表达式,使用变分原理或加权余量法将微分方程离散求解。由于有限单元求解的速度比有限差分法和有限体积法要慢上许多,所以在大部分CFD软件中并未得到广泛的应用。在常用的CFD软件中,只有FIDAP软件采用有限单元法。
(3)有限体积法
有限体积法又称为控制体积法,其思路是先将计算域划分为许多个网格,并使得每个网格都有一个独立的控制体积,再将待求解的微分方程对每个控制体积均进行积分,这样就可以得到一组离散方程。有限体积法得出的离散方程要求因变量的积分对任意一组控制集都守恒,因此在整个计算区域上也得到满足。有限差分法仅在网格极其细密时,其求出的离散方程才能够满足积分守恒,而有限体积法即使在网格不是很密条件下,也可以显示出积分守恒。
四、总结
流体力学在众多基础学科中属于相对困难的一门,但其在航空工业中扮演着及其重要的作用。除以上介绍的内容外,流体力学还有相当一部分的分支和拓展延伸,许多新的算法也在研究中。
参考文献
[1].周兵. 计算流体力学中常用的控制方程离散化方法概述[J]. 产学研理论与实践 科技经济导刊, 2017, 21(01):146





