0引言
永磁同步电动机以其结构简单，体积小、功率因数高的优良特性，在交流伺服系统中应用广泛[1]。但永磁同步电动机是一种非线性、强耦合的控制对象，在直接转矩控制系统中存在磁链和转矩脉动大的问题[2-3]。
本文利用模糊控制和神经网络控制不依赖于被控对象的数学模型优点设计了双前馈模糊神经网络控制器(Dual Feedforward Fuzzy Neural Network，DFFNN)作为速度调节器，与永磁同步电动机DTC系统相结合。解决了传统PI控制器对非线性时变系统适应能力差及单前馈模糊神经网络（Feedforward Fuzzy Neural Network，FFNN）控制响应慢的问题。
1永磁同步电动机的数学模型
永磁同步电动机三相坐标系abc通过Clark变换和Park变换，计算得到同步旋转坐标系d-p轴的电压方程为
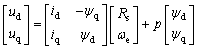（1）
式中：ud，uq分别为定子绕组在d-p轴的电压分量；id，iq分别为d-p轴电枢电流；P为微分算子；RS为定子绕组电阻；
为转子转速。
永磁同步电动机的转矩方程为
（2）
式中：Pm为磁极对数。
2单前馈模糊神经网络PI控制器设计
单前馈模糊神经网络控制系统结构如图1所示。
图1 单前馈模糊神经网络PI控制器
控制器输入变量分别为误差E和误差变化率Ec，经过单前馈模糊神经网络PI控制器计算出速度闭环的输出。E和Ec的模糊子集均为
。输入E和Ec的论域范围为[-3，3]，输出论域范围为[-6，6]。
3双前馈模糊神经网络PI控制器设计
双前馈模糊神经网络控制系统结构如图2所示。输出分别为KP，Ki，即PI控制器的最佳整定参数。其中，通过调试量化因子Se，Sde及比例因子SkP，Ski使输入值与输出值达到合适的控制范围，进而影响控制器的输出。
图2 双前馈模糊神经网络PI控制器
模糊神经网络控制器第一层为输入层，输入矢量为
，节点数为2，输出为
。
第二层为模糊化层。该层共14个神经元，前7个为误差E的模糊标记，后7个为误差变化率Ec的模糊标记。第j
个节点输出为
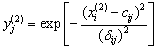
i=1，2；j=1，2...7 （3）
式中：
和
分别表示
的高斯隶属函数均值和标准差。
第三层为模糊推理层。共49个神经元，输出为
，k=1，2...49 （4）
式中：
为第j个输入；
为模糊化层与模糊规则层之间的连接权值。
第四层为输出层，实现解模糊操作。为模糊规则层所有输出信号的总和，即
，k=1，2...49 （5）
式中：
表示第三层模糊推理层的第k个输出量；
为第三层与第四层的权值。
本文利用误差梯度法来调整权值W，误差函数E表达式为
（6）
式中：
和
分别为第k个神经元目标输出和实际输出。
4仿真分析
通过Matlab/Simulink创建PMSM的DTC控制系统模型，具体参数为：极对数P=1，
，定子电感为
，转动惯量
。
分别对FFNN和DFFNN两个控制系统空载启动，给定1000r/min的转速。在25ms时给电动机加上
的扰动。
从图3-图6可以看出，DFFNN控制的系统在约4ms时转速达到稳定，较FFNN控制转速响应时间更短，在稳定转速下的转矩脉动保持在1.5N·m以内，较FFNN控制更加稳定，抗干扰性更强。
图3 基于FFNN控制的PMSM速度波形
图4 基于DFFNN控制的PMSM速度波形
图5 基于FFNN控制的PMSM转矩波形
图6 基于DFFNN控制的PMSM转矩波形
5结论
本文利用模糊神经网络的学习能力和自适应能力强的优点实现了基于双前馈模糊神经网络控制的永磁同步电动机直接转矩控制。从仿真结果看出该方法在额定转速下稳定运行，基本无超调，具有良好的动态特性。
参考文献：
[1] 王书博. 基于模糊神经网络算法的永磁同步电机位置控制[D].东北大学，2014.
[2] 唐红雨，刘贤兴. 基于无差拍的永磁同步电动机直接转矩控制方法研究[J]. 微特电机，2015，43(3):5-13.
[3] 杨建飞，胡育文. 永磁同步电机最优直接转矩控制[J]. 中国电机工程学报，2011，31(27):109-115.