零部件加工对几何量的精度要求很高,在测量时存在测量基准面的选择问题。基准对于计量人员而言具有重要的作用,主要包括基准直线、基准点以及基准平面,是明确几何要素关系的重要依据。不管是位置还是形状公差测量,若是缺乏基准,就会影响到结果的准确性。在实际测量中,时常会碰到基准和被测量要素不同面的情况,结合被测件的特殊结构,通过应用基准转化法,能够降低测量的难度。需要先引入中间基准,把实际基准转换成中间基准,测量得到被测要素和中间基准之间的关系,之后实施换算,明确被测要素和基准的关系,确保测量结果的可靠性。
1、基准转换原则
在这一操作中,中间基准选择具有重要的作用。结合设计基准,合理的选择测量基准,依据设计、测量及工艺基准一致的原则,尽量确保三者基准相符。如果要测量转换基准,需要考虑测量基准的方位及精度方面的要求,对于形状公差,直线要素一般依据其两端等高要求,调整相对于测量基准的位置,平面要素需要依据被测要素上距离较远的三点,调整到相对于测量基准高度一样的位置,回转面一般依据相距较远的两横向截面轮廓实施调整,尽可能到回转面轴线和回转系轴线相互重合;对于位置误差,应该对数据实施处理,进而得到终极结论[1]。
定位基准主要包括精基准以及粗基准,前者利用毛坯上通过机器加工的表面当作定位基准;后者利用毛胚上未经机械加工的表面当作定位基准,在选择定位基准时,应该选择没有加工的表面当作粗基准,若是包含几个不加工面,应该选择和加工表面位置精度要求最接近的一个面,确保二者间的位置精度。要想确保重要表面的余量均匀,应选择重要表面当作粗基准,在不要求重要表面加工余量均匀时,若是全部零件表面都要加工,可以利用最小余量表面当作粗基准。在测量工作中,应该依据基准重合原则落实,防止由于基准不重合而导致的测量误差问题,提升测量的准确性。
2、基准转换在几何量计量中的应用
2.1数显测高仪示值的检定
该设备是一种有效的测量仪器,在有关行业生产中得到了有效的运用,比如产品周期检定、生产验收都离不开这一仪器,由于实验室温度和湿度变化,使得实验中使用的平板精准度受到了影响。在检测工作中,需要先排除环境因素对实验的影响,然后检查检定方法的合理性。比如若是选择大理石作为基准平面,对标准块规进行测量,需要确保数显测高仪温度与量块温度相适应,在这种情况下才能开始检定操作。先将仪器测头打点清零,然后测量标准快规为100ram,获得的测量数值是100.0052ram。通过对比,结果存在误差。这时部分人员觉得是仪器精度不足,或是选择的基准面不够合理,无法简单的得到结论。通过调整之后,可以运用数显测高仪的功能,预先将实验方法设计出来,运用标准快速量具实施测量。明确参考平面之后,能够消除这一影响[2]。最后,对其他标准快速压力表实施测量。若是在实验过程中选择30毫米的规块,可测量快速标准快速规,先用高度计,把零点设置成30度,之后获得有关的数据,测量继续,测量规块变成100毫米,测量结果是100.0010mm,与标准一致。可以看到,平面度误差无法完全避免,即便测量易识别凹凸点,且凹凸点表面十分薄,但是在应用中还会影响到仪器的精准度,因此,应用标准量块,旨在解决量块的影响问题,利用仪器确保测量的可靠性及准确性。实践证明,这一方法能够用在工件测量中,优化测量的效果。
在计量中,要尽量确保测量、定位及技术基准一致,然而因为一些因素影响,导致结构的一部分无法依据基准实施叠加,设计与技术基准存在差异,一般要对设计基准进行优化,之后运用尺寸链原理,维度间的转换,确保电路其他元件的精确度,符合对测量尺寸的要求[3]。然而对于基准变化方法的优化,使得基准变化中的数据处理需求不断提升,各环的位置会增加,因此,数据转换及选择具有重要作用,这就需要结合设计基准合理的选择测量基准,依据三者统一的原则,确保三种类型数据相符,有需要时可以测量精准。线性元素要考虑要求精度及形状公差的测量及定位。
2.2激光干涉仪检测机床定位精度
将激光头安装到三脚架上,并且放置在地面上,测量反射镜固定在运动轴上,将分光镜固定到工作台上。比如某台金刚石加工中心实施定位精度工作,若是定位太小就会导致测量结果不能在反射镜中展示,对此,可以在机床和激光头间放置一个三脚架,将分光镜吸到三角架的台面,调整好光路之后进行测量。通过这样的方式进行测量,得到的结果会有一定的误差,对于数据的收集较为困难,在深入分析问题之后,发现并非是因为激光干涉仪导致的,而是分光镜放置的问题,因为运动时机床重心偏移,若是机床刚性还会引起整体倾斜的问题,使得系统有误差[4]。且分光镜会跟随机床的振动,无法确保干涉仪的稳定性,在呈现数据时一直跳动,无法稳定下来。
2.3指示表检定仪示值误差的检定
在实践中,需要在检测仪上安装电感测微仪的测量部分,被检测的检定仪在检定部分对准位置,电感测微仪的探测部分顶住测量面,并且把测量仪器数值调到0,把检定仪器的手轮及微分筒转到被检测的地方,便于电感测微仪有效的读出误差值。对于0-5受检点,误差主要包括正向误差和反向误差,前者分别是0.2,3.0,3.2,3.5,4.0,4.2;后者包括0.2,3.2,3.0,3.2,3.6,4.0。依据有关要求,仪器在5毫米内的误差要小于2m,检测存在问题。
在检定工作过程中,一般会把被检测的仪器测杆测量面作为基准面,电感测微仪为0,然而一些仪器长期使用,导致测杆的测量面会影响到平面度的精确性,且测量面中心有凹陷的问题,导致测量结果的准确性受到了消极影响。对此,在测量工作中,应该将一个测量块放到测量面和电感测微仪的测头间,其尺寸是1毫米,同时确保平面度精准,之后调整电感测微仪,准确的对0位,然后重新进行检定,得到的数据有所调整,对于0-5受检点,正向误差分别是0.0,0.3,0.5,0.5,1.0,1.5;反向误差分别是0.1,0.5,0.5,0.6,1.0,1.2。基于重新测量,明确仪器误差为1.5m,与指标相适应,检定结果合格[5]。
2.4同轴度测量
其是测量中的一个重要问题,国际上对轴线的同轴度公差有清楚的界定,然而在检测工作中,由于测量方法选择不合理,导致出现结果误差显著以及重复性差的情况。在同轴度测量中,要想提升准确性,就要巧妙的运用基准转换法。
2.4.1以螺纹为基准的位置度测量
从下面的图1中可以看到这种测量方法的实例,图纸要求测量相对于A基准的同轴度,然而由于该基准属于外螺纹,不能直接用其当作基准实施测量,常见的方法包括:
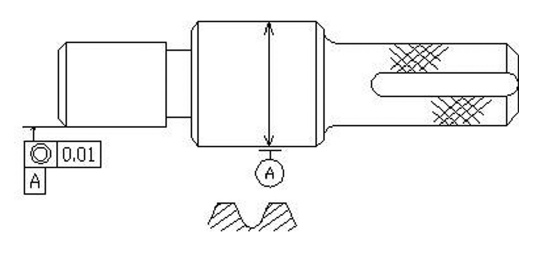
图1以螺纹为基准的测量实例
第一种方法:结合螺距选择最佳三针,把两根三针分别放入螺纹内,需要注意的是,为了便于之后的操作,应该将两根三针放入间隔几个螺距的齿内。之后把被测件放至于0级大理台平台上,工作人员要用一只手按紧被测件螺纹段的上部,另一只手操作千分表实施测量,通过这样的方式可以得到测量的结果。
可以看到,运用了基准转换法,把该基准的螺纹中径转换成大理石平台,可以提升工作的效率,然而对工作人员具有一定的要求,需要具备丰富的操作经验,若是操作不熟练,则要安排两位人员一起配合,确保测量结果的可靠性。
第二种方法:将加工基准当作测量基准。由于加工基准和图纸要求的A基准不同,在测量操作中,需要结合螺距,合理的选择最佳三针,然后在被测件同一轴切面上,运用杠杆千分表测量要求部位以及螺纹部位,转动被测件一周,测量四个轴切面,分别获得相应的测量数据,最大差值就是要求的测量结果。在运用这一方法之前,需要先清洗顶针孔,防止出现误差较大的问题[6]。
这一方法就是对A基准的螺纹中径进行转换,变成加工基准,也就是顶针孔,操作起来较为便利,为了获得可靠的结果,需要对得到的数据实施有效的处理。
对比这两种方法,从基准转换角度来说,第一种方法基于三针转换基准,第一种方法把基准转换成加工基准;立足于操作步骤层面来说,第一种方法操作起来较为简单,第二种方法的操作步骤较多;从操作人数层面来说,第一种方法在操作中需要1-2人,第二种方法只需一人就可完成操作;从操作难易程度角度来说,第一种方法的操作难度较大,而第二种方法容易操作。
在几何量计量工作中,上述两种是常用的方法,每种方法的优点和缺点各不相同,这就要求计量工作人员结合实际情况,合理的选择基准转换方法,提升几何量计量工作的效率及效果,保证测量的精准度。
2.4.2应用三坐标
从下面的图2中可以看到测量孔的同轴度,图纸要求测量Φ24的孔相对于A基准Φ20孔的同轴度。在测量中由于孔端面短以及两孔相距较远,导致工作难度较大。运用三坐标测量机对孔进行测量,需要选用圆柱测量。由于孔端面短,使得圆柱两个测量截面间距很小,两个孔间的距离较远,运用这一方法测量得到的同轴度,对采点的敏感系数很大。对此,如果基准截面和被测截面距离很大,要求用这一方法测量同轴度,就要通过基准转换的方式来实现,利用公共轴线当作基准线。在基准圆柱以及实测圆柱上测量在中间位置的截面,得到两个孔中面截面的连,将其作当作基准轴线,计算出基准圆柱和被测圆柱相对基准轴线的同轴度,其最大值就是误差范围。
需要注意的是,在实践中要避开影像测量结果的槽和油孔等,因为各种外观缺陷,如毛坯气孔、沟痕以及划伤等,会影响到测量的准确性,容易引发误差问题,需要人为去掉外观缺陷之后,再对测量结果做出合理的评价。
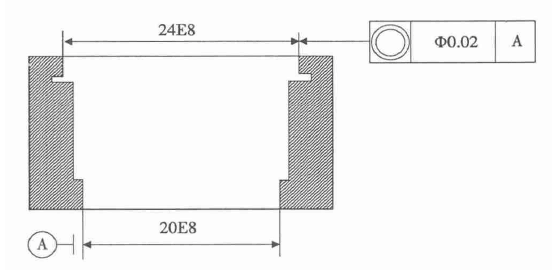
图2 测量孔的同轴度
结语:
综上所述,几何量测量较为复杂,零件的类型较多,在测量工作中,若是遇到常规测量无法解决的问题,就要运用基准转换法,提升测量的准确性及可靠性。因此,计量人员应该准确掌握基准转换法,做好几何量计量工作。
参考文献:
[1]陈晓东,张方明.几何量计量器具在铁路货物装卸作业中应用初探[J].铁道技术监督,2021,49(12):23-25.
[2]张星勤,刘娜. 浅谈工业生产中的几何量计量器具[C]//.2020中国航空工业技术装备工程协会年会论文集.,2020:80-82.
[3]本刊讯.第十八届国防系统几何量计量技术交流会顺利召开[J].计测技术,2019,39(02):10.
[4]李高之.基准转换在几何量计量中的运用分析[J].科技风,2018(21):20.
[5]袁雯雯.浅议几何量计量的发展与趋势[J].民营科技,2018(03):35.
[6]高思田,李琪,施玉书,李伟,黄鹭.我国微纳几何量计量技术的研究进展[J].仪器仪表学报,2017,38(08):1822-1829.





