前言:
在高中数学教育中,构建数学建模思想的重要性不容忽视。数学建模是一种将现实世界的问题转化为数学问题的过程,它不仅能够帮助学生理解数学概念,还能够培养他们解决实际问题的能力。通过数学建模,学生可以将抽象的数学知识与具体的现实情境相结合,从而更深刻地理解数学的实际应用价值。本文将深入探讨如何在高中阶段有效地构建数学建模思想。
一、高中数学构建数学建模思想的重要性
(一)数学建模能够激发学生的学习兴趣。传统的数学教学往往侧重于理论知识的传授,而忽视了数学与现实世界的联系。通过引入数学建模,学生可以在解决实际问题的过程中体验到数学的魅力,从而提高学习数学的兴趣和动力。
(二)数学建模有助于培养学生的创新思维和解决问题的能力。在构建数学模型的过程中,学生需要运用所学的数学知识,结合实际情况,进行分析和推理。这个过程不仅锻炼了学生的逻辑思维能力,还激发了他们的创新意识。通过不断的实践和探索,学生能够学会如何将理论知识应用于实际问题中,从而提高解决问题的能力。
(三)数学建模能够帮助学生更好地理解和掌握数学知识。在解决实际问题的过程中,学生需要深入理解数学概念和原理,这有助于他们巩固和深化所学的知识。同时,数学建模还能够帮助学生发现数学知识之间的内在联系,从而形成更加系统和全面的数学知识结构。
(四)数学建模是培养学生综合素质的重要途径。在数学建模的过程中,学生不仅需要运用数学知识,还需要具备良好的沟通能力、团队协作能力和信息处理能力。这些能力的培养对于学生未来的学习和工作都具有重要意义[1]。
二、高中数学构建数学建模思想的策略
(一)借助问题情境
在高中数学教学中,构建数学建模思想是一项至关重要的任务。这一过程不仅要求学生掌握基本的数学知识和技能,更重要的是培养他们将数学知识应用于实际问题的能力。为了有效地实现这一目标,教师应当巧妙地利用问题情境来引导学生进行数学建模。情境教学是课堂教学常见方式,高中数学教师可运用问题情境开展建模教学,促使学生在探索、思考、提问、分析以及建模等一系列过程中高效解决问题,并对所学知识产生深入理解,锻炼思维能力。教师需要积极思考该如何引领学生学习,因此需要在为学生传授知识和技能的同时不断延伸自身知识储备深度与广度[2]。
例如,在学习“均值不等式定理”相关知识时,教师设置以下问题:“某超市在中秋节开展促销活动,为吸引客源,共设计以下三种降价销售方案:①首次打a折,第二次打b折销售;②首次打b折销售,第二次打a折销售。③两次销售均打折,请问,上述三种打折销售方案哪种最为划算。”学生经思考和相互讨论后得出以下解题要点:即对ab与大小进行比较。上述题目紧贴学生现实生活,教师为学生设置抽象概括且符合学生实际情况的问题情境,以生动形象的方式为学生呈现生硬抽象的均值不等式定理。大部分高中数学应用题在解答中都需运用均值不等式,故而,创设紧贴生活的问题情境导入新知识能调动学生探究知识积极性,更能活跃学生数学思维。其次,挖掘纯数学问题生活原型,不断增强学生建模意识。现实生活生产中蕴含大量数学问题,将数学知识和技能结合现实生活生产能增强学生灵活运用知识能力。例如,某制造厂今年一共生产近5万吨产品,如果平均每年产量高于上一年10%,请问从今年起在几年内能实现总产量30万吨目标?教师在讲解题目时要先指导学生分析前几年产量,即今年为5万吨,明年则是5+5×10%=5×1.1,那么后年则为5×1.1+5×1.1×10%=5×1.12,学生在观察中归纳总金额公比q=1.1后构建等比数列模型。虽然上述解答过程较为缓慢,然而能促使学生深入理解问题,提升建模核心素养能力。
(二)借助信息技术
事实上,现实生活中涵盖大量数学知识,学习数学知识目的之一也在于更好地解决实际问题,尤其会应用几何图形、函数、方程等知识,故而运用“互联网+建模”能直接降低题目难度,提高解题效率。检验和完善解题模型是数学建模思想下重要思维环节之一,类似于常规学习总结与检验,有利于帮助学生充分把握自身在数学建模活动中出现的解题错误和认知不足,促使学生高效理解和掌握不同类型解题模型使用条件,并在归纳总结、反思、纠正等一系列活动中建立正确建模认识,为提升建模素养做好铺垫[3]。
例如,在学习“数列”相关知识时,教师结合现实生活常见的银行存款本息计算设计问题,需要学生结合真实银行存款月利率与本息计算公式对某个周期内本息总和进行计算,在此过程中应用数列知识。教师在教学过程中运用信息技术为学生建立模型并基于此凸显数列模型思想,促使学生运用等比数列求和规律分析和解决实际问题。与此同时,鼓励学生独立思考问题,再以小组形式相互讨论分析,遇到疑惑之处可运用平板和互联网中的学生端口发送给教师,随即教师为学生实时答疑解惑,还可在学生小组讨论时参与其中,提升学生学习效率。
(三)在作业中融入建模理念
课后作业应讲究高效性与质量性,为此教师要将建模思想融入作业中,提高作业的合理性,将原本学生作业形式单一、内容陈旧、难度过高等弊端,转变为更为锻炼思维能力、探索意识、自主性等方面[4]。
以“统计”方面内容为例,当课堂教学结束后,教师可以对学生留下这样一道作业题目:在智能产品与日常学习的影响下,青少年逐渐出现视力减弱的问题。为了更加直观的了解高一学生视力情况,随机抽查某个学校100名高一学生的视力情况。如下图。由于调查人员的失误,部分数据出现丢失的情况,但知道前4组的频率成等比数列,后6组的频率成等差数列,设最大频率为a,视力在4.6至5.0之间的学生数为b则a,b的值分别是多少?
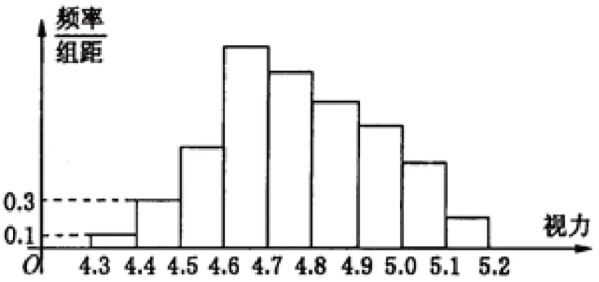
设计作业问题后,则引导学生运用统计与等差、等比中数学知识的数学模型解决问题,明确数学问题中的数量关系,并运用相关的公式解决问题。这样一来,不仅强化学生对数学知识的记忆,同时可以提高数学模型解决问题能力,有利于学生的数学模型构建。在丰富作业设计内容的同时,提升学生解题意识与数学思维,使学生更好的学习数学知识,并达到灵活运用的目的。
结语:
综上所述,高中数学教育中构建数学建模思想的重要性不言而喻。通过数学建模,学生不仅能够提高学习数学的兴趣,还能够培养创新思维和解决问题的能力,更好地理解和掌握数学知识,以及提升综合素质。因此,教师应当重视数学建模在高中数学教学中的应用,提升数学课堂教学意义,为学生提供更多的实践机会,帮助他们构建数学建模思想,为未来的学习和生活打下坚实的基础。
参考文献:
[1] 刘洋, 刘春红. 高中数学建模活动和数学探究活动的实践路径[J]. 天津教育, 2022(2):3.
[2] 韩玉灿. 新课程背景下高中数学建模教学的研究[J]. 高中数学:高中版, 2022(2):2.
[3] 黄展伟. 高中数学建模教学及强化方式分析[J]. 神州, 2020(15):2.
[4] 高建芳. 基于高中"数学建模"素养的教学设计与评析[J]. 海风, 2022(2):1.
