1 前言

高温气冷堆闭式Brayton循环具有安全性高、成本低、对环境友好等优点，多采用氦气作为循环工质，循环热效率高（~45%）、功率密度大、结构紧凑、且系统比质量小，是空间核反应堆动力循环的理想选择^[1,2,3]。要正确描述热力循环系统的运行状态，必须考虑所选混合工质热物性对机组变/稳态运行的影响机制，因此获取完整且精度可靠的氦气热物性数据就成为了首先要解决的基础性课题^[4,5]。

导热系数是表征物质传热能力的一种输运性质，是Brayton循环中换热器设计过程中的必要参数。目前氦氙工质的导热系数数据缺乏、现有公开发表的文献数据不能覆盖氦气冷却反应堆工作温/压范围、不同来源数据间存在偏差大和一致性差等问题^[6,7,8]，无法满足反应堆稳态和瞬态特性准确模拟的要求。因此，本文通过动态光散射法测量了氦气373.15 ~ 773.15 K和0.1 ~ 5 MPa范围内的热扩散率，并通过多参数状态方程计算了氦气的密度和比热，从而获取氦气的导热系数。

2 实验原理

动态光散射法测量导热系数的原理可以描述为：当相干光透射处于宏观热力学平衡状态的透明流体样品时，可以从样品的各个方向观察到散射光。在流体混合物中，散射过程受物质浓度的微观涨落控制，且浓度涨落的衰减与热扩散系数有关。利用光散射法对散射光强进行时间分析，可以得到这些平衡过程的信息。根据实验获得的散射光强随时间变化的相关函数，即可计算待测流体的热扩散系数，如图1所示。在外差混频探测条件下，时间相关函数可以写成：

  （1）

式中：G(2)(τ)为光子时间相关函数；τ为时间；A、B为拟合参数；τC为时间常数，表征浓度涨落弛豫到平衡值所用的平均时间，受热扩散系数a控制：

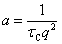  （2）

式中：q是散射矢量，与真空中入射光的波长λ0和入射角Θi有关：

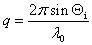  （3）

图1 时间相关函数

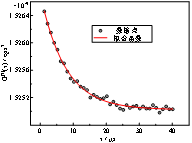
图2 动态光散射法实验系统

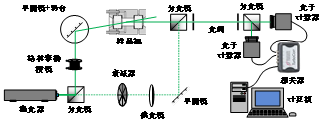
动态光散射实验系统如图2所示，该试验系统的散射光路由激光器、可调衰减器、格林泰勒棱镜等器件组成，利用高精度电动转台和平移台控制散射角度和散射中心的位置，使探测光以一定角度入射试验本体。利用双光子技术器采集即可获取两个自相关和一个互相关函数光谱信号，从而获取微弱的散射光强度随时间变化的涨落过程。

热扩散率测量的不确定度由波长、入射角和衰减时间的不确定度组成，其相对不确定度分别为2.17·10-5、1.25·10-4和0.007。因此热扩散率实验系统的不确定度为0.7%，当取置信因子k = 2，置信度为95%时，实验系统的扩展不确定度为1.5%。实验装置及原理的详细介绍，本课题组之前的文章有过详细报道^[9,10]。

3 实验结果与分析

本文利用动态光散射法测量了373.15 ~ 773.15 K和0.1 ~ 5 MPa范围内氦气的热扩散率，实验数据如图3所示。通过对比分析实验数据可以发现，沿等压线，氦气的热扩散率随温度的升高而增大；相同温度下，氦气的热扩散率随压力的增大减小，且压力越小热扩散率随压力的变化约明显。热扩散率与导热系数间存在关系a = λ/ρcp，根据多参数状态方程计算密度ρ和比热cp^[11]，可计算得到氦气的导热系数。如图4所示，在373.15 ~ 773.15 K和0.1 ~ 5 MPa的温度压力范围内，氦气的导热系数随温度升高明显增大，且近似成线性变化规律；在该压力范围内，压力对氦气导热系数的影响很小，高温条件下，随着压力的升高，氦气导热系数略有增加；低温条件下，压力对氦气导热系数的影响可以忽略。

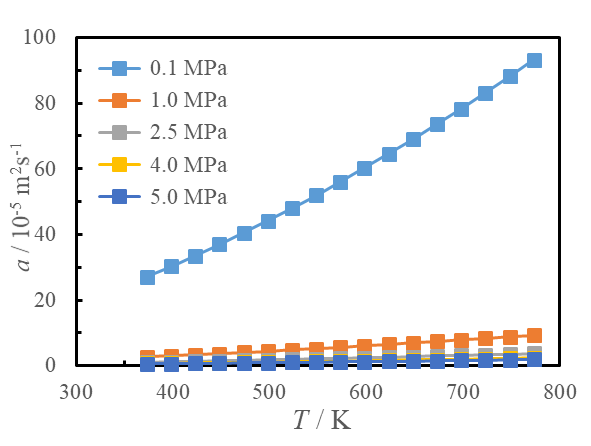
图 3  氦气热扩散率

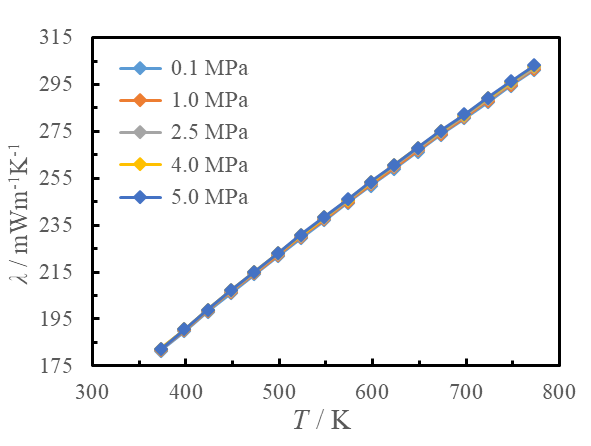
图 4  氦气导热系数

4 结论

本文使用动态光散射法对373.15 ~ 773.15 K和0.1 ~ 5 MPa的温度压力范围内氦气的热扩散率进行了测量与分析，并计算了该范围内氦气的导热系数。结果表明，沿等压线，氦气的热扩散率和导热系数均随温度的升高而增大，且近似成线性变化规律；在相同温度下，氦气的热扩散率受压力影响变化明显，压力越大，热扩散率约小，而导热系数受压力影响较小，随着压力的增加，氦气的导热系数略有增大。

参考文献

[1] Olumayegun O, Wang M, Kelsall G. Closed-cycle gas turbine for power generation: A state-of-the-art review[J]. Fuel, 2016, 180: 694–717.

[2] Tian Z, Jiang B, Malik A, 等. Axial helium compressor for high-temperature gas-cooled reactor: A review[J]. Annals of Nuclear Energy, 2019, 130: 54–68.

[3] No H-C, Kim J-H, Kim H-M. A REVIEW OF HELIUM GAS TURBINE TECHNOLOGY FOR HIGH-TEMPERATURE GAS-COOLED REACTORS[J]. Nuclear Engineering and Technology, 2007, 39(1): 21–30.

[4] Wang J, Gu Y. Parametric studies on different gas turbine cycles for a high temperature gas-cooled reactor[J]. Nuclear Engineering and Design, 2005, 235(16): 1761–1772.

[5] Pérez-Pichel G D, Linares J I, Herranz L E, 等. Potential application of Rankine and He-Brayton cycles to sodium fast reactors[J]. Nuclear Engineering and Design, 2011, 241(8): 2643–2652.

[6] Vargaftik N B, Vasilevskaya Yu D. Thermal conductivity of helium at temperatures from 300 to 6000 K[J]. Journal of Engineering Physics, 1982, 42(3): 296–299.

[7] Jody B J, Saxena S C, Nain V P S, 等. Thermal conductivity of helium: A probe for the repulsive wall of the interatomic potential[J]. Chemical Physics, 1977, 22(1): 53–58.

[8] Jain P C, Saxena S C. Transport properties of helium in the temperature range 400–2300 K[J]. Chemical Physics Letters, 1975, 36(4): 489–491.

[9] Chen J, Xing H, Zhan T, 等. Measurement of thermal diffusivity of ethanol from (293 to 564) K and up to 10 MPa in vicinity of the critical point[J]. Fluid Phase Equilibria, 2022, 552: 113276.

[10] Zhang Y, Chen Y, Zhan T, 等. Measurement of thermal diffusivity for carbon dioxide (CO2) at T = 293.15–406.15 K and pressures up to 11 MPa by dynamic light scattering (DLS)[J]. Fluid Phase Equilibria, 2018, 474: 126–130.

[11] Gomez-Osorio M A, Ortiz-Vega D O, Mantilla I D, 等. A formulation for the flow rate of a fluid passing through an orifice plate from the First Law of Thermodynamics[J]. Flow Measurement and Instrumentation, 2013, 33: 197–201.