1 引言

迭代学习控制是智能控制算法的重要分支之一，这种新型学习控制方法在本世纪八十年代由日本学者Uchiyama提出。迭代学习控制适用于具有某种重复运动性质的被控对象，可实现有限时间区间上的完全跟踪任务。迭代学习控制主要用于解决轨迹跟踪和误差调节这两大类问题。各类控制方法层出不穷，但绝大多数控制技术都只能对系统期望输出进行渐进跟踪，于是如何实现完全跟踪成为了一个研究热点。迭代学习控制的主要思想是给定一个期望轨迹，对控制系统进行控制，由系统输出与期望轨迹的差值来修正控制信号，新的控制信号再对系统进行控制，最终提高系统的控制性能。对于具有非线性、时变性等动态特性的系统，其控制器设计很难准确，其控制精度更是难以保证。迭代学习控制能够处理这类无法建立精确模型的系统，并且不需要大量的先验知识。

神经网络理论在智能控制、模式识别、机器视觉等方面都发挥了不同程度的作用。神经网络具有很强的逼近非线性函数的能力，将这种能力运用到智能控制中，可以发挥更大的作用。本文介绍利用神经网络拟合迭代学习控制器参数，从而提高系统控制性能的方法。此时神经网络的主要作用是根据控制输入信号和输出误差不断调整神经网络的权重，由权重计算出新的控制器参数，重复运行实现对期望轨迹的完全跟踪，其很大程度弥补了因学习律参数固定造成的迭代学习次数多、收敛速度慢等问题。

2基于神经网络的迭代学习控制的系统结构

对于大多数控制系统，其主要任务就是寻求控制使得输出达到所要求的形式。本文所举出的控制任务是使偏差尽量小( 为期望输出)，随着迭代次数K的增加，最终使系统实现完全跟踪。如今被广泛应用的迭代学习控制律有P型、D型、PD型和PID型。利用神经网络的非线性逼近能力来拟合优化控制器参数，较为常用的结构是BP神经网络，但具有更好的逼近能力和学习能力的RBF神经网络优化参数已被提出。本文选用PD型迭代控制律、RBF神经网络进行分析说明。

此系统结构可以分为迭代学习控制器和神经网络两部分，如图1。

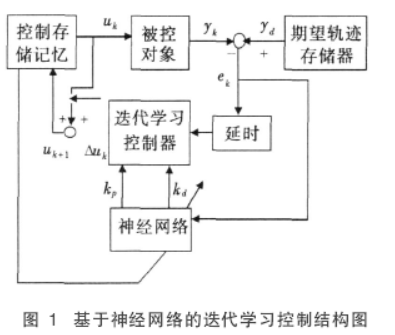
设计PD型学习律对被控对象进行迭代学习控制，其中设置控制器参数为K_P和K_d。选取RBF神经网络，它由输入层、隐层、输出层组成。通过梯度下降法调整神经网络的权值系数，拟合计算出新的控制器参数K_P和K_d，重复对学习律进行修正，再观察输出是否达到控制要求。整个学习过程可以概述为：在第K次运行时，由控制信号得到一个输出信号。计算期望输出与的偏差，将得到的误差和放到神经网络中拟合计算出新的K_P和K_d。将其代入控制律，得到下一次的输入信号，进入一个重复的过程，直到实际输出逼近期望轨迹。

3 问题解决与展望

（一）提高重复任务跟踪精度

迭代学习控制已被应用于机械手控制，使机械手能够完成固定路线“抓取”、“放置”之类的动作。在这一系列动作中，机械手按照所期望的轨迹进行操作是需要保证的。虽然可以将每个操作过程分解为一个简单控制问题，利用前馈和反馈方法减小误差。但系统模型不能确定，这会造成反馈过程计算量不准确等问题，最终无法实现轨迹的完全跟踪。

尽管模型不确定性普遍存在，对于重复性任务如何提高跟踪精度。记重复的次数为K。从概念上讲，在重复执行第K+1次时可使用前重复运行时采集到的数据，包括系统实际的输入输出数据以及控制信号。如果合理利用这些数据，则可在以后的重复过程中减少错误的机会。理想情况下，当K无限增加时，跟踪误差也将减小到零。这是一种基于迭代学习的机械手控制方案，因为可以将过去的数据引入任务执行之间的交互，它也适用于重复控制框架。

（二）提高学习过程收敛速度

迭代学习控制的思想很容易掌握，但如何保证其收敛性是探索过程中最重要的一点。在提出新的学习律时，必须考虑解决与之相应的迭代收敛性分析问题。不难想到，给出学习律的形式是迭代学习控制器的设计问题，其中学习增益的设定也是工程实现时不容回避的控制器设计问题。在被控对象动力学特性完全未知时，分析推断出的收敛性条件并不能直接用于学习增益的选取，只能给出一个较大的范围，我们一般会在这个较大的范围内进行自行设定，但准确度是无法保证的。神经网络对控制器的拟合，很大程度上降低了这种自设定的盲目性，并从新的角度来优化这个问题。

（三）减少初态偏移问题带来的影响

在具有重复运行性质的系统中，进行重复定位操作很容易产生初态偏移。运行过程中的干扰和噪声等也会对系统的重复操作产生影响，从而无法保证系统最终能够实现收敛。针对这个问题有学者也从稳定性和鲁棒性两个方面对系统进行分析。由于迭代学习控制系统收敛性一般是在无扰条件下存在，在系统具有初态偏移、状态扰动等情况下实际运行可能并不收敛。利用神经网络拟合功能优化重置控制器参数，从一定程度上减少了干扰带来的影响，使系统达到收敛更加容易。

4 参考文献  

[1] 孙明轩,黄保健．迭代学习控制[M]，北京：国防工业出版社，1999.

[2] 王丹凤,李书臣,翟春艳,邢宜春.基于神经网络参数优化的迭代学习控制算法[J].河南科技大学学报(自然科版),2008(06):42-44+110.

[3] 郝晓弘,段晓燕,李恒杰.基于BP神经网络的迭代学习初始控制策略研究[J].计算机应用,2009,29(04):1025-1027+1031.

[4] 刘晏辰,贾英民. 基于神经网络的机器人系统的鲁棒迭代学习控制[C]//2006中国控制与决策学术年会论文集.,2006:1450-1453.

[5] 高兴航,李晓光,邵诚,姬忠良.基于神经网络优化的迭代学习控制方法的研究及应用[J].吉林化工学院学报,2006(01):50-55.

[6] D. Zhang, Z. Wang and T. Masayoshi, "Neural-Network-Based Iterative Learning Control for Multiple Tasks," in IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 9, pp. 4178-4190, Sept. 2021.

[7] 陈杨,林辉.基于神经网络的迭代学习控制参数拟合[J].计算机仿真,2003(07):62-64.

[8] 刘欢培. 不确定非线性系统的迭代学习控制与自适应神经网络控制[D].浙江工业大学,2005.

[9] D. A. Bristow M. Tharayil and A. G. Alleyne "A survey of iterative learning control" IEEE Control Syst. Mag. vol. 26 no. 3 pp. 96-114 Jun. 2006.

[10] 王跃灵,沈书坤,王洪斌.不确定机器人的自适应神经网络迭代学习控制[J].武汉理工大学学报,2009,31(24):135-138+144.

[11] 张囡,李元明.机械手RBF神经网络滑模迭代学习控制[J].电子世界,2013(10):219-220.

[12] A. Weckenmann,X. Jiang,K.-D. Sommer,U. Neuschaefer-Rube,J. Seewig,L. Shaw,T. Estler. Multisensor data fusion in dimensional metrology[J]. CIRP Annals - Manufacturing Technology,2009,58(2).