学起于思，思源于“疑”。疑为学之始，知为学之成，思为成之器。没有思考就没有疑问，质疑也是思维（问题是思维的一种成果形式），指对客观情境产生是什么或为什么的好奇；通过可否或假设提问，改变原有条件而产生新的观念和方法的思维方式。知识的建构过程其本质就是思维的过程，只有经历不断质疑的探索和深思熟虑的思考，学习才会真正发生。

一、案例分析

初建《组合图形的面积》（人教版五·下）教学：问题导向放手自主尝试生成多解方案，合作探究解读思路与方法，再组织学生对众多解法进行研究。通过分类、命名达成方法结构策略；对比分析寻找策略共性，实现策略结构思想。教学层层递进，学生拔节成长，不失为一堂成功的教学设计。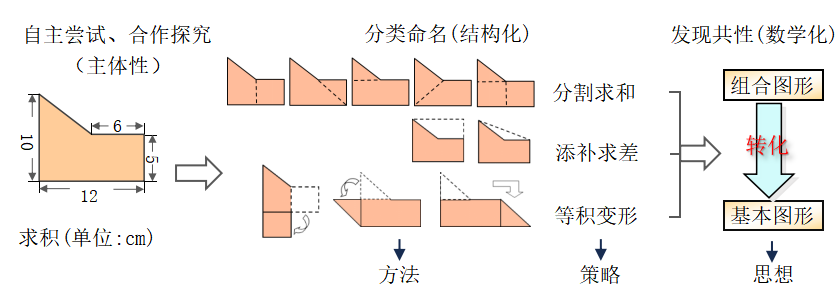

多次实践发现添补和变形的方法难以生成。老师“教”优生“凑”，虽然解决是什么和为什么的问题，但没看到凭什么。凭什么学生会想到添补求差？又凭什么会生成等积变形？没有经历发自心底独立的质疑与思考，就没有深度的意义理解。接下来的结构化、数学化变成教学技术流程，育人内涵大打折扣。看似完美，实则美中不足。

原因何在？读图。看出显性信息读出隐蔽关系，带着质疑读活图形的“构成”。“这个图形就一定是组合而成的吗？”教和学都缺少质疑思维，知识发生发展没有生长点。

数学是系统性很强的学科，知识联系紧密而结构存在。新的知识、方法与思想都有其发生、形成和发展过程。用数学的眼光观察情境、事例、背景提出问题；用质疑的思维对原认知做出可否或假设提问，从而驱动思考与探究活动产生新的观念和方法。传授数学知识是基本的教学任务，沿着知识的形成过程，启迪思考发展思维培育关键能力，形成解决实际问题的智慧才是数学教育的价值所在。

问题的能力？

二、培养质疑思维的方法

（一）创设情境，质疑是什么、为什么

客观世界存在无穷的秘密和问题，发现问题探寻秘密认知这个世界，适应并改造环境更好的生活是人的基本能动性。知识来源于生活，从知识发生角度出发，创设情境激活学生好奇的认知心理，思考质疑“是什么？”和“为什么？”以及刨根问底追溯更多的“为什么？”充分发挥数学在形成人的理性思维、科学精神和促进个人智力发展独特的育人价值。例如：

情境创设要贴近学生的生活经验，激发求知欲激活思考产生疑问，推进数学知识的探究活动。真实生活情境具有较强的综合性，跨学科开发项目化、主题式学习成为可能。

（二）关联推衍，用“可否”或“假设”质疑

知识依存于经验，当认识一个概念或习得某个方法时，学生习惯于关联思维，由此及彼类推演绎，用“可否”或“假设”思考质疑。组合图形可以看成几个基本图形“组合而成”（经验），可否看成是从某个更大图形“分解而来”呢？（质疑）。整数、小数加减法都强调列竖式计算（经验），为什么分数加减法却只字不提呢？假设用竖式该怎么计算呢？（质疑）。知识发生、发展的形成过程，就是质疑思考、实践探究的过程。转换同位概念和转换相反意义概念思考是小学生质疑思维的显著特征。

1.转换同位概念质疑

同位概念是相对上位概念和下位概念而言的，没有上下逻辑关系却有相同属性的类概念。老师表扬某同学：他从边的角度不仅看出了线段的长短，还看出了它们的长短关系，真了不起！其他学生会立刻转换概念，从点、角、形观察思考有什么信息？边与边之间有长短关系，还有什么关系呢？

又如《有趣的搭配》教学中两次精彩对话：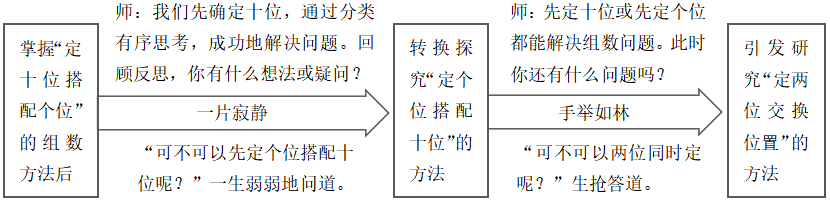 

定个位搭配十位，定两位交换位置的组数方法是在定十位搭配个位经验基础上，转换同位概念通过可否或假设质疑“长”出来的。既能看到学生清晰的思维脉络，又能感受知识发生、发展的形成过程，还能支持分类思考有序排列的思想方法建构。

整数、小数、分数；长度、面积、体积；条形统计、折线统计、扇形统计；…… 类似的同位概念、系列知识还有很多。遵循知识的一致性、结构化原则，注重知识形成的过程，久久为功，培养学生质疑意识发展学生质疑思维。

2.转换相反意义概念质疑

合与分、大与小、相向与相背等概念有明显的相反意义。转换相反意义概念引发思考质疑是小学生的又一个思维特征。

重建《组合图形的面积》教学，开课有这么一段对话：^[1]

师：看到“合”字你会想到哪个字？

生：分。因为“分”是“合”的反义词。

师：好！老师看到了你敏锐的逆向思维。其实“合”与“分”不仅是一对反义词，还是生活中很普遍的现象。正所谓分久必合，合久必分，事物的发展总是在分与合的交替转换中发展的。由此，为我们认识事物、解决问题打开了一条思路：通过分（部分）来认识和解决合（整体）的问题；通过合来理解和运用分的特征。

从组合图形的核心“合”入手打开话题激活逆向思维，联系生活事理导向分合转换认知世界、解决问题的思维方式。发生想象、思考、质疑，使创见性图形理解，多解方法产生有了凭什么的依据而成为可能。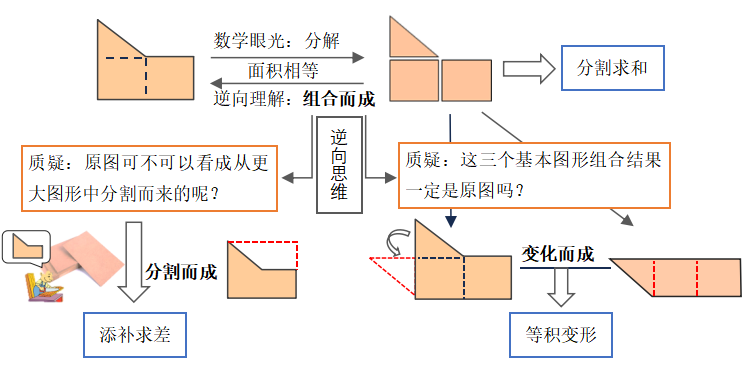 

读图驱动空间想象，读懂图、读活图发展空间观念。转换相反意义概念，分合交替使“想”有方向、“疑”有出处、“长”有依据。部分视角（分）积淀读图经验，读出图形组成部分的形状，数量关系、位置关系；整体视野（合）创见图形理解，读出组合而成的方式，想象分解而成的可能，思考变化而成的存在。

（三）构建学习场，促成疑问顿生

知识依赖于背景。沿着知识的形成过程，构建结构紧密、活力充沛、关系和谐的学习场，使学生心智自由地思考与质疑问难。

友好关系与和谐氛围崔生思考、质疑。疑问意味着不懂、不会。不确定所提问题是否靠谱，冒着被嘲笑的风险提问，“安全感”是学生首先考虑的因素，特别是有过挫败经历的学生，几乎只答不问。保护好奇心、求知欲，营造心理自由、情感自在、思维自主的“学习场”是质疑的前提条件。

仔细观察、认真思考方能产生高质量疑问，质疑又意味着自信，彰显学习力量。独立思考，交往互动，思维在碰撞中闪耀火花。思维活力充沛的探索氛围是生成问题和解决问题的关键。

认知和知识具有背景依赖性，灵感、顿悟、疑问总是离不开一定的环境氛围，只有在特定情境下才能激发某个感受，顿生某个问题，形成某种认知。注重知识的形成过程，以知识学习为载体，润育数学疑思之萌蘖，发展学生质疑思维，培育学生创新意识，培养学生关键能力。

三、结语

总之，在数学教学中，我们应注重知识形成的过程，引导学生积极质疑、思考和探究。通过创设情境、关联推衍和构建学习场等方式，培养学生的质疑思维，激发他们的创新意识和探索精神。让学生在知识的海洋中畅游，不断成长和进步，为未来的学习和生活奠定坚实的基础。

参考文献：

[1]《小学数学结构化例谈》（谢强 《四川教育》总第850期 2024.7.）

[2]赵娜娜.小学数学优质课堂构建的实践探究[J].试题与研究,2024,(22):144-146.

[3]魏艳艳.小学数学核心素养视野下高阶思维能力的培养[J].读写算,2024,(26):74-76.‌