引言:海洋平台是海洋油气资源开发的主力军,也是海上生产、生活的重要基地,如果海洋平台结构出现问题,不仅会造成巨大的经济损失,还会给平台上的工作人员带来生命威胁。但海洋凭条结构复杂、体积较大,在进行结构优化设计过程中存在很多的问题,只有选择最合适的方法,才能够保证海洋平台的稳定性。
一、海洋平台结构特点
海洋平台是一种高出海面的工程结构,可以分为固定式平台和移动式平台。固定式平台可以分为导管架型、塔型、重力型等各种结构形式,而移动式平台可以分为自升式、半潜式,浮船式和张力腿式等结构形式。作为海洋资源开发的基础设施,大部分时间情况下,都处于复杂和恶劣的环境条件下,在实际发展过程中,环境腐蚀、材料老化、构件缺陷都困扰着平台发展。因此,需要对海洋平台结构进行优化设计,建立形成优化算法模型,系统的分析平台结构情况,切实提高可靠性以及动力响应灵敏度,为海洋资源开采提供科学可靠的保障。
但从目前情况来看,在优化设计过程中,还存在很多问题。第一,结构问题。结构构件大多数为批量生产,相应的结构单元剖面尺寸一般设计为离散。但从灵敏度的角度来看,基于离散型变量和混合型变量构成的优化系统并不合适。第二,优化目标问题。常规的优化设计模式主要针对的是平台可靠度、使用寿命以及可靠度演化规律等内容。但是新时期,对平台的灵敏度提出了新的要求,传统的方法很难分析此类问题。第三,平台复杂问题。海洋平台经历的荷载非常复杂,以辽东湾为例,海洋平台需要承受及冰激振动、波浪、协同作用、风载、冰撞以及腐蚀疲劳等荷载。
二、海洋平台结构优化策略算法
由上可知,必须要建立起全新的海洋平台结构优化策略算法,在计算离散变量、荷载特征以及混合变量的基础上,进一步实现灵敏度、最优选型等方面的计算。
为了保证全新的海洋平台结构优化策略算法能够满足各方面内容的需求,选择改进的序列二次规划以及序列线性规划方法进行计算。利用约束函数、目标函数中的导数信息,将问题转换为箱形规划问题。在此基础上重复求解,直到迭代收敛,并且最优设计。平台结构设计过程中,形状和尺寸这两个类型的设计非常关键,但也是结构设计中最为困难的内容。但在改进的序列二次规划以及序列线性规划方法基础上,可以实现分层处理,两个阶段下的尺寸优化后,将此时得到的形状变量设定为常数。在此基础上,通过重复求解和迭代收敛,得到最终的数据,完成优化设计。
相比较形状优化工作而言,拓扑优化设计难度更大,在传统的设计方案中经常会选择基结构法。通过这种方法可以更好的观察拓扑变化。从理论的角度来讲,任何一个构件都可以从结构中删除,都可以成为优化的对象。但是对于具体的海洋工程平台而言,每一个构件的都会受到海洋生产要求以及环境要求的限制,在优化设计中,无法随意删除优化。以平台的桩腿为例,桩腿根数有固定的数量,不能随意增减。只有无限接近于零的小数才能够被列为拓扑优化的对象。
海洋平台结构的动力优化是优化设计过程中重要环节,但是传统的设计方式中,对海洋平台的动力优化问题的计算并不完善。但在生产中因为实际需要,出现动力不稳定的情况,就需要将一般动力常数到海洋平台结构设计中,这就涉及到了动力优化问题。需要注意的是,动力优化并不一定在同一个算法中进行,还存在非常复杂的情况,而且具有高度非线性特点,这就需要对动力的情况进行仔细的计算。为了完成动力优化工作,实现海洋平台结构动力响应的灵敏度,必须要对于算法进行全面分析。在优化工作过程中,不同海洋平台之间结构约束条件存在一定的差距,对算法的收敛性要求较高,必须要提取出最佳的优化求解算法。
总的来看,海洋平台结构的优化设计受到多方面条件因素的影响,在优化设计的过程中,需要综合考虑多方面因素的问题,科学引用其他改进技术,完成结构优化。
一般性的结构优化设计数学模型表示如下:

改进的序列二次规划以及序列线性规划方法数学模型表示如下:
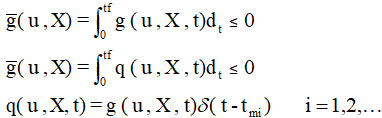
在上述两个公式中,,m和n分别代表着约束条件和设计变量的个数,X为设计变量组成的向量,f(X)为目标函数,gj(X)为约束函数,XL和XU表示的是X的下界和上界。g(u,X,t)≤0表示的是瞬态相应约束条件[1]。
三、海洋平台结构动力响应的灵敏度分析
海洋石油工程的作业平台工作环境非常复杂,海面作业非常容易受到海浪、大风等恶劣天气甚至地震等不可抗力因素的威胁。这些都给海洋平台财产安全构成了极大的威胁,同时也给海上作业人员的带来非常高的风险。因此,要最大程度地保障海洋平台结构的稳定安全,每个海洋平台结构都要经过全面的优化和设计后才可以得到应用,确保其明确工作时能够有效应对不同的危险,在保护好凭条自身的同时,确保工作设备的安全,减少不必要的损失。
在确定具体的改进后算法的基础上,进一步对海洋平台结构动力响应的灵敏度展开分析,主要从稳态响应和瞬态响应两个角度展开分析和研究。在推导灵敏度分析算法的过程中发现,采用瞬态动力响应的时间差分格式求解这种方法计算灵敏度较为简单。以直接法为例,在直接法中,需要对每一个设计变量进行求解,采用瞬态动力响应的时间差分格式求解,可以最大程度简化计算过程。而在伴随法中。需要计算每个约束求解式,进而分析相应的数据。两种方法应用的方向并不相同,需要根据实际情况进行选择。比如:在约束条件较多,设计变量较少时,可以采用直接法进行计算,反之则选择伴随法计算。
以渤海石油公司的海洋石油开采平台为例,平台采用了导管架海洋平台结构动力优化设计方法,在此基础上,借助前文提出的算法,计算分析海洋平台结构动力响应的灵敏情况。该凭条的位置特殊,经常会冰荷载的周期作用。在这样的情况下,想要对平台结构进行动态响应分析和优化设计难度较大。根据各项参数数据,最终计算得到了结构两个阶段的自振频率为0.88Hz,对比实测数值0.87Hz接近。在此基础上,进一步计算结构动力响应,从结构最大的节点动位移响应计算结果来看,峰值为0.42cm。
导管架平台结构优化设计模型是目前应用最为广泛的一种优化方式,主要的目的在于降低结构重量,提高结构的稳定性。在不改变单元圆管截面内径的基础上,根据截面性质,设计了四组数据。按照上述两种方案分别进行计算,其中动位移响应约束条件分别为0.5cm和0.4cm,根据计算设计结果来看。结构重量分别降低了40%和27%。不仅满足约束条件,整体稳定性也到了大幅度提高[2]。
总结:综上所述,本文从海洋平台结构存在的问题入手,建立了结构响应优化算法模型,并且计算得到了在瞬态动力响应和结构稳态响应的灵敏度数值。在此基础上,结合实际案例展开进一步分析研究,从多个不同的优化设计方式来看,本文设计的算法能够在海洋平台结构动力响应优化设计中应用。
参考文献:
[1]赵玉良,董胜,姜逢源,等.渤海导管架平台的冰激振动响应分析[J].海洋湖沼通报,2019(4):22-29.
[2]秦晓宇,袁奎霖,钱缘.海洋平台圆管构件抗撞性能数值分析[J].中国海洋平台,2019(4):59-64.





