0 引言
“保障不足”和“保障过剩”一直是各级装备保障部门的业务痛点。这不仅增加了保障成本，而且还降低了保障效益。当务之急就是研究如何提前预测可能发生的装备故障。目前常用的预测技术分为三类：基于失效物理模型、基于寿命分布模型和基于数据驱动模型。原理上，前两者构建模型需要相关条件假设，有些甚至与实际偏差较大。相比之下，归功于相关性理论和大数据技术的发展，基于数据驱动的故障预测优势更明显，技术更成熟，应用更广泛。与此同时，该领域研究也越来越深入，各式各样的方法和模型层出不穷，可惜研究成果转化应用的却不多，特别是针对基层部队装备故障预测的成熟模型就更少。因此，本文基于装备故障历史数据，探索并构建与之相适应的预测模型。
1 确定预测思路
1.1 预测需求
当前装备保障不精准的问题主要表现在维修人员、器材等保障资源的短缺。这无疑延长了装备的修复周期，进而影响了装备战斗力的恢复，究其原因还是装备故障的不可预知性。如果能够有效地预测出装备故障数量、时间甚至某个部件，就可以有力地指导保障资源的筹措工作，使装备维修和资源保障无缝对接；那么装备保障工作就很可能摆脱传统的事后维修，从而转变为预防性维修，大大提高了装备保障的时效性和精确性。
1.2 预测的数据来源
通过梳理分析装备保障数据来源，发现可以用于故障预测的唯有装备故障数据。该数据的定义字段一般有故障装备、故障时间、故障现象、故障原因及修理工时等，本质上属于时间积累的历史数据。因此，针对此类与时间有不确定相关性的数据，运用以时间序列分析为主的方法去构建预测模型比较合适。
1.3 预测对象
基于数据驱动的故障预测，如何确定预测对象，前提是要掌握数据来源的本质与特点。装备故障数据记载着整个单位所有装备故障情况，装备和故障是每个故障条目的两个主要定义字段。部分装备可能会重复发生故障，但也不可能每件装备都会发生故障，这是装备故障数据的客观现实。如此，现阶段的故障预测是不可能将故障精确预测到某个装备或部件，而是应该偏向于宏观预测，比如预测下个周期内可能发生的装备故障种类、数量或故障率。
综上所述，基于历史数据的装备故障预测，是以工作周期内的装备故障记录为数据来源，通过建立以时间序列分析为主的预测模型，最终实现装备故障总体种类、数量或故障率的预测。
2 ARMA-BP组合预测模型
为弥补单一模型的缺陷，提高预测精度，本文采取组合模型方式，将时间序列的ARMA模型和BP神经网络模型融合为一种新的预测模型。其具体建模流程如图1所示：
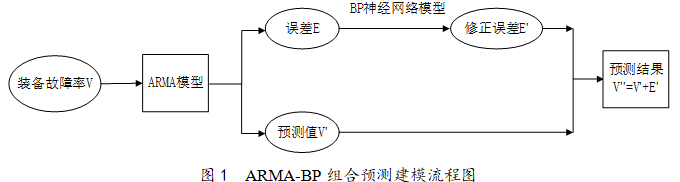
假设某类装备故障的发生率为，首先运用ARMA模型对序列的进行预测，预测结果为，则与真实值的误差序列：，其中可能包含了原始序列中的非线性关系；再采用BP神经网络模型对误差进行预测估计，得到修正后的误差记为，于是组合模型的预测结果可以写为：。
3 实证分析
为本文“装备故障预测”的研究需要，以某单位为例，将该单位在2004年-2019年的装备故障数据进行初步统计分析，得到某类装备故障发生率如表1所示。然后分别应用ARMA模型和ARMA-BP组合模型预测2012年-2019年8年来的装备故障率，并与真实值对比分析。
3.1 ARMA模型预测分析
3.1.1 平稳性检验
在建立ARMA模型之前，需要对原始数据进行平稳性检验。本文采用Eviews10.0软件进行统计分析，分别得到三种模型的ADF检验结果，其T检验统计量的显著性P值均大于0.05，这表示接受原始序列存在单位根的原假设，即该原始数据不是一个平稳的时间序列，需要进行平稳化处理。
这里采用一阶差分法对原始数据进行平稳化处理，并绘制差分后的数据时序图（见图2）。从图形上看，该数据大致平稳，不存在任何显著趋势，基本可以判定为平稳数据。
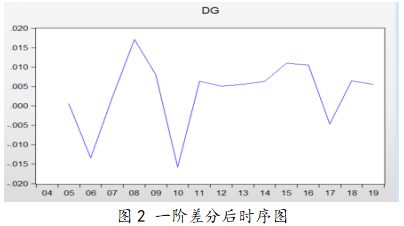
仅凭图形判断过于主观，为确认该数据的平稳性，必须进行差分后的再次ADF检验，T检验统计量明显小于三种置信水平的临界值，显著性P=0.0021，远远小于0.05。因此，时序图和ADF检验结果共同说明，原始数据经一阶差分后，满足平稳性要求，可以进行建模。
3.1.2 模型的定阶与参数估计
由于自相关系数与自偏相关系数均在2阶后趋于零，所以定阶后的模型可能为AR(1)、AR(2)、ARMA(1,1)、ARMA(1,2)、ARMA(2,1)、ARMA(2,2)等，经不断尝试，最终确定模型为AR(2)。其中，常数项为0.003808，显著性P=0.0254；滞后二阶的系数为-0.57618，显著性P=0.0066，均通过显著性检验；但模型是否为最终预测模型，还须对模型残差进行相关性检验。
3.1.3 模型检验与预测
根据ARMA模型假设，最佳预测模型的残差序列应该为白噪声。若残差序列不是白噪声序列，说明残差序列还有信息没被提取，需要进一步改进模型。同样地，再做出AR(2)模型残差序列的自相关和偏自相关分析。
由相关分析得出，模型的误差序列的自相关系数和偏自相关系数均未超出置信带，并显示在延迟1阶至12阶Q检验统计量的P值均显著大于0.05，说明该模型提取信息充分，误差序列可以判定为白噪声序列。所以，AR(2)模型是显著有效的，可以用于预测。
3.2 基于BP神经网络模型的误差预测分析
经过ARMA模型预测后，误差序列可能还存在非线性部分，根据ARMA-BP组合预测思路，下面运用BP神经网络模型对误差序列进行预测。而构建BP神经网络的关键是设定好各层节点数、隐含层层数和激活函数，因为不同的参数设置所构建的BP神经网络，其训练效果是有优劣之分的。
由于ARMA模型误差序列不是标准的输入输出数据，本文采用累计故障率方法生成训练样本的方法，将表5的误差序列前5个数据作为输入，第6个数据作为输出，建立如表1所示的8组训练样本。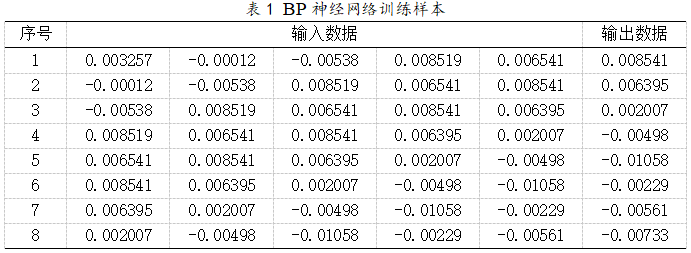
本文利用MATLAB训练BP神经网络模型，采用典型的三层网络结构，即隐含层数目为1。再根据表1的训练样本，输入层、输出层节点数可确定为5和1。至于隐含层节点数,参照公式（4），以 为1至10的随机数，经过反复多次试验，最终选定隐含层节点数时拟合精度较高。参照以往研究经验，选取LOG-SIS型函数为隐含层的激活函数，PURELIN纯线性函数为输出层激活函数，训练效果最佳。而网络训练函数采用基于L-M的TRAINLM函数。此外，还需设置其它BP神经网络参数：目标误差，最大训练次数为，学习率，训练步长选择0.1，各层之间的初始连接权值和输出阈值由网络自动选取。待该网络构建后，经过8次训练与学习达到精度要求，得到2012年-2019年的预测值，将其与ARMA模型预测误差对比分析，如表2所示。
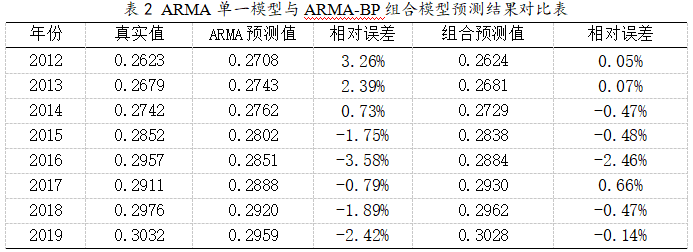由上表2可知，相比单一的ARMA预测模型，基于ARMA-BP神经网络组合预测模型的相对误差有明显下降，其预测值更接近真实值。因此，实例证明了基于ARMA-BP神经网络的组合模型比单一的ARMA模型预测效果更好，预测精度更准确。
4 结束语
本文针对装备故障不可预知导致的装备保障不精准问题，首先分析了部队装备故障预测的现实需求；其次结合积累的装备故障历史数据的特点，确定了基层部队装备故障预测的基本思路；最后为兼容不同模型的优点，将时间序列的ARMA模型与BP神经网络模型进行组合构建，并完成了该预测模型的实例验证工作。结果表明：该组合模型比单一模型的预测效果更好，预测结果更精确，适用于基层部队的装备故障预测。