九十年代初,原国家教委基础教育课程研究中心严士健教授强调了“数学教学应联系实际”,“要重视从实际问题中建立数学模型,解决数学问题,从而解决实际问题这个全过程”。于是出现了一些“应用题”,“情景题”,“开放题”。但这是远远不够的,虽然这些问题多源于生活,但与实际问题比较起来,实际问题的不确定性、模糊性、涉及范围的广泛性、没有标准答案、需要反复修正等特点是不具备的。为了更好地培养数学应用的能力,我们把问题延伸到了课下。
问题解决同时包括解决数学内部和外部的问题,而“数学建模”则偏重于数学外部问题的解决,可以看作问题解决的部分领域。作为问题解决的一种模式,数学建模更加突出对原始问题的分析、假设和抽象的数学加工过程;数学工具、方法、模型的选择和使用过程;模型的求解、验证、再分析、修改假设、再求解的迭代过程。它更完整地表现了学数学和用数学的关系。大阪教育大学松宫哲夫先生提出了CRM(Composite Real Mathematics)型课题学习的过程如下图
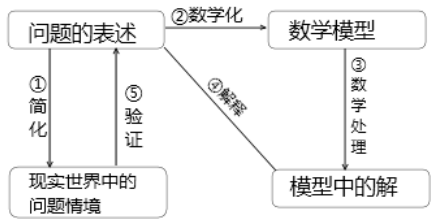
由于学习了《理解数学》--张思明,我们也大胆的设计了一定的课外的数学问题。由于书中主要是针对高中的学生设计的问题,我们又查阅了大量的资料,针对初中生的问题可用的很少,于是我们研究教师集体备课,最后决定给学生提供方向,由学生们自己设计问题,没想到学生给了我们大大的惊喜。以下出示两组学生的问题解决报告:
案例一:
主题为“租房与买房中的数学问题”的课题。这是一个数学应用、建模、探究的场景素材,老师不必给出具体的问题,只要把场景给出,学生们自己发现和提出数学问题,而后解决这一问题。下面是一组学生给出了如下报告:
研究课题:
一对25岁夫妻买或租一套四中100平米的学区房住到65岁总价对比。
我们课题小组成员的分工是:
设计研究范围:关润涵
搜集相关数据:高薇
分享展示:高薇 李嘉益
撰稿:高薇 李嘉益
绘制函数图像,课题分析:关润涵 高薇 李嘉益 曹芳瑞 战泓多 齐子莹 刘语嘉 郎妍慧
我们解决问题的思路,前期的学习和资料工作,分析和求解的主要过程:
在研究之前,我们首先确定了研究对象。确定研究对象为房产问题之后,我们围绕房产这个主题进行展开。首先,我们设定主人公是共有存款二十万的二十五岁夫妻,由于考虑到未来孩子的上学问题,我们选择了学区房作为我们的研究对象,并且选择了100平米这个数字,最后确定了我们的课题“一对25岁夫妻买或租100平米学区房住到65岁的总价对比”。
确定了课题之后,我们询问了珲春市中桥房产工作人员,了解到100平米的房子,首付需要20万,可分为十年和二十年月供;租房一个月需要1600元左右,于是我们将问题分为三组,分别是将20万元存在银行租房和十年月供以及二十年月供。
接着我们对数据进行初步处理,租房每月需要交付1600元,因为租房组将20 万存入银行,经搜索后,我们以年利率2.75%为基准进行研究。买房组由于没有准确数值,我们查询百度资料大概了解到,十年的月供为2931.57元,二十年的月供为1701.59元,由于我们能力有限,所以四舍五入分别为2930元和1700元,租房与买房都需要交付水电费,所以这里我们不做研究,买房每年需要多交付物业费和取暖费,于是经过讨论,这个被加入了买房组研究范围之内。
我们用到的数学知识和方法有:
1.一次函数
2.正比例函数
3.分段函数
中间过程的描述:
我们一共绘制了三个图像,两个一次函数图像和一个正比例函数图像。分别代表租房,十年分期和二十年分期。买房需一年缴纳物业费和取暖费2650元,我们按一个月220元,租房不需缴纳。买房需缴纳二十万元首付,将租房省下的二十万元人民币存入银行的利息另计算。我们建立平面直角坐标系,以住房的月数为x轴(单位:月),所花的总价钱为y轴(单位:万元)。
1.租房:我们假设租房,不需交暖气费和物业费,只需要交每月1600元房租,因此,租房的总价构成正比例函数y=0.16x。
2.十年分期付款:10年分期的月供,我们按2930元计算,并且我们在买房子时首付20万元。在我们需要还房贷时,每月月供加上物业费,共3150元,并且还有已缴纳的20万首付。所以前120个月(x大于0,小于等于120),所花总钱数解析式为y=0.315x+20。在第120个月时,我们共花费了57.8万元,在120个月之后我们不需再缴纳房租,但是还需要缴纳每月220元物业费,所以x大于120时,y=0.022(x-120)+57.8,也就是y=0.022x+55.16。
3.二十年分期付款:20年的分期月供,我们按照1700元计算,和十年分期一样,仍有首付20万,每月物业费220元,每月共1920元。前240个月(20年),可得解析式为:y=0.192x+20。在第240个月时,共花费66.08万元,在第240个月之后,同样不需缴纳房租,但需缴纳物业费。可得解析式:y=0.022(x-240)+66.08,化简可得:y=0.022x+60.8。
最后将三个解析式用图像表达(如下图)
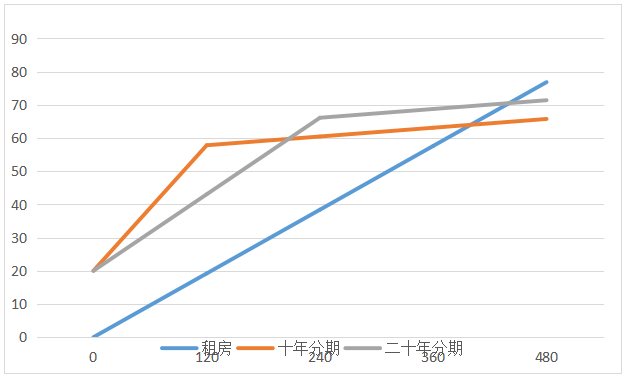
误差分析和评价:
1.根据网上信息,租贷30万元人民币,分十年付款,每月应缴纳2931.57元,在计算时,我们按照每月2930元计算;分二十年付款,每月应缴纳1701.59元人民币,在计算时,我们按照每月1700元计算。
2.每年物业费和取暖费,按照现在的价钱,每年在2650元左右,我们合计每月220元(租房不需要缴纳物业费和取暖费)。
3.我们所计算的房价都是按照现在的价钱,并且不考虑房屋贬值问题,理想计算租房价钱不变。
4.我们在计算时,忽略了租房买房都需要计算的水费,电费,交通费用,装修改造房屋价钱等。
5.我们在计算过程中,忽略了不同位置房价不同的因素,统一按照平均房价50万人民币计算。
6.假设在买房贷款时期,每个月的月供不变;假设将租房存入银行的20万人民币全部存入中国银行,定期存款年利率为2.75%不变,每年存入的本金都按照20万人民币计算,并且不购买任何理财产品。算得一年利润为5500元人民币,40年也就是22万元。
中间结果的描述:
我们最后求得解析式,因为要从25岁住到65岁,一共居住40年,也就是480个月,我们将X等于480分别带入解析式中,最后可以得到:租房一共花费76.8万元,十年分期共65.72万元,二十年分期共71.36万元。因为我们将租房省下的20万元存入银行,我们按照他每年只存二十万,并且银行利率为2.75%不变,不购买任何理财产品。最后到第40年可得利息共22万元人民币。用租房的钱减去利息,最后得租房总金为54.8万元。通过对比,我们可以得出租房最省钱。
工作收获和体会:
本次实践提高了我们团队合作能力,使我们通过实践更加了解社会,更懂得了团结一致,共同进步的道理,也让我们更深刻地掌握了一次函数、正比例函数及分段函数的知识点。学会在生活中运用数学知识,利用数学建模的思想解决生活中可能遇到的问题。我们更建立了一种将实际问题建立成数学模型来进行计算,对我们所要研究的问题进行假设,建立出合理的数学模型(例如一次函数图像,二次函数图像,反比例函数图像等),让我们能对自己遇到的实际问题进行预估,得出最终结果,以便于解决现实中的问题。
得到的帮助和致谢:
1.感谢珲春市中桥房产相关工作人员,为我们提供四中学区房,100平米购房的价格和租金的价格,以及我们所能办理购房贷款的年限。
2.感谢杨立新老师和王晶老师为我们提出建议:在最后对比总价钱时,应当将租房省下的二十万首付钱存入银行,在最后计算租房总价时扣除20万元人民币存入银行40年的总利息,得到实际租房40年的总价钱。
主要参考文献:
1.百度“车呗理财”30万元人民币的房贷,贷十年,贷二十年利息数额。
2.知乎 2020年各银行最新存款利率。
案例二:
珲春电影院性价比结果分析
本次我们选择了三家电影院进行了分析,分别是新天地、百货以及今夏。
首先是三家电影院的会员制度,三家的会员票价都是24元/张,原价都是60元/张。同时,新天地和今夏还拥有儿童票价,都是30元/张。三家电影院都是一百元起充,同时新天地的充会员制度为充二百送一百,充三百送三百,其余两家为自己本身所充钱数。
对于这样的会员制度,我们首先要定下一个标准,在经过我们一番深思熟虑过后,我们认为一年内可能出的好电影不会超过二十五个,并且人们繁忙的工作以及学业不允许人们去看那么多的电影。所以我们将电影场数上限定在了25场。接下来就要分成两个方面来考虑,第一种是成人购票:在一年只看一场的情况下,不冲会员是最为合适的;二到四场时,充一百的会员最为合适;五场时,充一百会员并用原价看一次电影最为合适;六到八场时,充二百的会员最为合适;九到十二场时,冲二百的会员最为合适;十三场时,冲二百会员并用原价看一次电影最为合适;十四到二十五场时,冲三百会员最为合适。以上是根据新天地的优惠制度来说的,如果是今夏或百货则要从九场为一分界线,之后的场数所花的钱都要比新天地多出一百到三百不等。所以从这一方面来看,新天地的会员制度在大于等于九场时开始显现出自己的优势,在小于九场时三家电影院则是一样的。
第二方面则是儿童购票,原理和成人购票大抵相同,所以我便直接说结论了:在一年看一到三场或五到七场时可以选择新天地或者今夏;在一年看四场或八场时三家可以凭自己喜好选择;在一年看九到二十五场时选择新天地最为合适。
无论从成人角度来看还是儿童角度来看,新天地无疑是最为省钱的。我们又像同学们去调查了有关于这三家影院自己的看法,认为新天地环境好的有10人,服务态度好的有15人;认为百货环境好的有5人,服务态度好的有0人;认为新天地环境好的有35人,服务态度好的有35人。综上所述,如果单纯的为了省钱,我们推荐大家去新天地观影;如果想要追求更高的观影感受,我们比较推荐今夏。以下是我们对于本次探究的评价及误差分析:
总结评价与误差分析:
1.在我们本次调查中,由于为了简化购票的问题,将三家电影院的会员卡余额存储期限,其中现代百货所持有的会员卡是终身制,但金夏和新天地两家的存储年限均为一年,但考虑到现代百货制度的多方面劣势所以并没有将其算作在内具有一定的误差。
2.考虑电影场数的最值问题时,将一年所看的最大场数定为25场,但实际对问题本身影响不大,按照每个月看2-3场计算,25属于较为准确的折中数,但仍具有一定误差。
3.最后一点便是关于充值会员卡方面在不同节假日金夏有不同的优惠政策,并且近期金夏并无任何充值优惠,具有较大误差。
结论:如果单纯考虑价钱的问题去欧亚,价钱实惠,观影效果也不差。如果想要追求较好的观影设施和条件,去金夏,有舒适的座椅和温度恰好的空调。不建议去百货,价钱较贵,没有任何优惠,观影质量和服务态度较差。
运用到的数学知识与方法:分段计费,条形统计图,调查问卷。
得到的帮助和致谢:三家员工的热心解答和帮助;杨立新老师的指导
参与者:9-11 程琳 9-15 刘宗仁 9-11 王禹涵 9-15 余夕来(按姓氏首字母排列)
数据整理与分析:王禹涵 程琳 刘宗仁 余夕来
数据归纳及撰稿人:刘宗仁 余夕来 王禹涵 程琳
这种教学实施中,教师提供一个自然场景作为数学建模的素材,这个自然场景中可能蕴含很多问题,具体提出哪方面的问题需要学生自己观察、思考。学生在这样的情况下常常会发现诸多老师没有注意到的问题,提出一些让人眼前一亮的新的想法和问题。这样的形式更加锻炼学生发现问题,提出问题的能力。
这种教学实施形式适合:(1)对数学建模有初步认识,或者对如何发现,提出问题有初步认识的学生;(2)基础较好,思维已经活跃起来的学生。这里我们要注意,学生的思维活跃很大程度上受其思维习惯的影响,学生按部就班的跟随老师走,只想老师提出的问题,难以自己提出自己的想法,思维刻板等种种表现并不是天生的,而是在长期的教育中形成的思维;反之,思维也是可以通过教育来激活的,我们的教师要不断地创造条件,鼓励和促使学生多一些自己的思考。
3.3学科间的研究性学习
这种方式需要集学校的力量或集学年的力量,由所有参与的学科教师共同研发一个大问题,解决这个问题需要各学科知识进行整合,学科教师针对大问题中,需要本学科知识的部分提出相应的问题或解决问题的建议,由学生组成小组,分工完成。最后得出相应的问题题研究报告。值得注意的是,这个大问题没有标准的答案,没有最终的结论,只有同学在参与本次课题的感受。这个感受可以是针对研究过程的,可以是对研究结论的,也可以是透过研究感受到的社会关怀,人文关怀等多方面的内容。
这种方式的特点是选题和素材的收集、研究的过程及成果的表述都由学生自主完成。这种形式中学生学习的自由度最大,但并不意味着教师可以撒手不管,而对老师的指导有更高的要求。这种情况下,老师的指已经在前面的介绍过,这里就不赘述了。
学生全自主的选题方式,基本上适合于数学建模学习的最后阶段,老师的指导要贯穿学生的整个建模过程,指导原则需要启发、诱导,不可包办,不可代替学生思考和拿主意。
参考文献:
[1]张思明,理解数学--中学数学建模课程的实践案例与探索,福建,海峡出版发行集团福建教育出版社,2012.
[2]史宁中,数学基本思想18讲,北京,北京师范大学出版社,2017
[3]李希贵,为了自由呼吸的教育.北京:高等教育出版社,2005.
作者简介:吉林省珲春市第四中学数学老师,现担任班主任,本科学历





