引言
高等数学是理工科数学系列课程的龙头,其课程建设的好坏影响着众多课程建设的水平与质量[1]。高等数学不仅为学生后继课程的学习和研究奠定基础,而且还在于培养学生的抽象能力、逻辑思维能力、运算能力等方面的作用,是其他课程无法替代的。但是高等数学具有高度的抽象性、严密的逻辑性和广泛的应用性,以及各个知识点之间具有紧密的联系性和隐藏性,导致部分学生对高等数学产生了厌倦心理。又因为有些学生数学基础比较薄弱、高等数学是高等学校的“网红”挂科课程,知识点抽象且零散,内容多课时少,在有限时间里只讲授新知识导致学生对该门学科学习逐渐失去信心和兴趣[2]。因此,如何有效梳理高等数学的知识点,提高教学质量和效果,激发学生学习的主动性和创造性,培养学生分析问题和解决问题的能力,是高等数学教学中面临的主要问题和挑战。
目前思维导图作为一种思维工具,在医学领域和中小学课堂教学运用比较成熟。但知网检索中关于思维导图在高等数学教学应用文献仅有20篇,表明思维导图在高等数学教学中的应用未引起足够的关注。本文拟探讨思维导图的内涵、思维导图应用于高等数学课堂的必要性、通过案例分析探讨思维导图在高等数学课堂的应用、以及思维导图在理工科教学中的意义。
1. 思维导图的内涵
思维导图(The Mind Map)最初是20世纪60年代英国心理学家东尼
博赞(Tony Buzan)发明的一种笔记方法,他认为传统的笔记有如下缺点:埋没关键词、不易记忆、浪费时间、不能有效刺激大脑。而思维导图是一种用图像来进行辅助记忆的有效工具,强调发散性思维与逻辑思维能力。它将图像与关键词相结合,通过颜色、线条、符号、数字、文字等方式刺激大脑,建立网络结构,促进有效记忆[3]。
思维导图被发现以来,在各个学科各个领域都有了广泛的应用,被称为21世纪全球革命性思维工具。思维导图的基本特征和特色如下所示:
思维导图基本特征:(1)注意的焦点清晰地集中在中央图形上;(2)主题的主干作为分支从中央向四周放射;(3)分支由一个关键的图形或者写在产生联想的线条上面的关键词构成,比较不重要的话题也以分支的形式表现来,附在较高层次的分支上;(4)各分支形成一个连接的节点结构[4]。
思维导图的特色主要在于防止思维中断,保持思维方式连续感,并且能更好地把握内容的整体性和方向性,便于加强记忆以及方便复习。思维导图的特色使学习者整合新旧知识,使前后知识关联,成为有机统一整体,从而促进有效学习,帮助学生形成逻辑严谨、有机统一的理论知识体系,方便学生全面把握和深化理解众多知识点,提高课程学习效率[5]。
2. 思维导图应用于理工科教学的必要性
(1)思维导图满足高等数学课程人才培养目标[6]
高等数学课程目标有专业目标和思政目标,两个目标的达成具有协同效应、相辅相成。专业目标:培养学生掌握知识与技能、过程与方法;思政目标:塑造学生情感态度与价值观、数学素养与创新思维。
在高等数学教学中应用思维导图,一方面:利用图形的形象思维与抽象思维,不仅可以激发学生的学习兴趣,还能进一步激发学生的发散思维,促进对基础知识、基本理论、技能的掌握,达到增强记忆、提高学习效率和创造性解决问题的能力,达成课程专业目标;另一方面:利用思维导图梳理各章节知识及联系过程中,教师能够在更高层面上挖掘和提炼蕴含在各章中的思政元素,将思政点、思政线、思政面串联起来,将思政教育润物细无声融入教学,达成思政育人的目标。
(2)思维导图教学满足高等数学课程特点
高等数学是理工科必修的基础课程,内容涉及数学发展史、大量的物理背景、线性代数内容、常微分方程内容以及辩证思维和高度的抽象逻辑思维。教学内容零碎,公式和概念多,抽象难以理解,以及课时压缩,学生学习高等数学很吃力。
思维导图作为一种辅助思考和总结工具,能有效的将教学知识点整合,简化学习过程;思维导图的线条多变,图文并茂,有利于学生抓住重难点,降低学习的难度和枯燥性。
因此,在理工科教学中合理的使用思维导图工具可以把零散、抽象、独立的公式以及知识条理化、可视化和系统化。不仅有助于教师的教,而且有利于学生的学,促进了理工科学科教与学的相辅相成。
3.思维导图在理工科教学中的应用
2017年五四青年节,习近平总书记在中国政法大学考察时重要讲话中指
出:要教育引导青年师生训练思维方法、提升思维能力,养成系统思维、辩证思维、创新思维的习惯。因此在理工科教学中不仅要求课堂知识脉络清晰,而且在育人过程中需要培养和提升学生系统思维、创新思维等。研究表明,思维导图不仅是一类总结工具,还是一类思维工具。结合教学实践,下面将从课前—课中—课后探讨思维导图在理工科教学中的应用:
(1)思维导图在课前预习的应用,有助于调动学生学习积极性[7]
学生课前预习是保证课堂教学有效性的重要环节。课前教师通过主题形式发布章节或者小节的重难点或者关键词,学生对课前预习比较有目的性。通过制作思维导图形式,学生会主动深入研究课本中相关知识内容,通过连线将与主题相关的概念和命题连接成思维导图,在这个过程中能够有效激发学生学习的主观能动性,使得听课更加有主动性和针对性。
以《高等数学》中的极限为例,学生课前预习制作思维导图步骤如下[8]:
(1)根据下次讲课内容,列出关键词;(2)将这些关键词按照一定的逻辑顺序列出来;(3)将重点和难点做好标识。制作思维导图如图1所示:
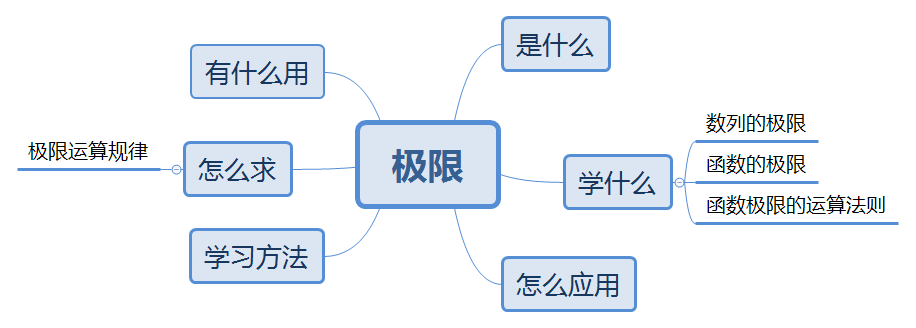
图1 课前预习—极限思维导图
(2)思维导图在备课中的应用,有助于提高课堂教学效率
备课是决定教学质量的关键环节。教师在备课时使用思维导图,一方面可以作为教学准备的工具和手段,整理备课思路、梳理教学内容、确定教学目标、确定教学方案、安排教学环节等,思维导图如图2所示;另一方面,针对教学内容方面:有助于教师理清教学思路,把握重难点,快速把握教学环节,提高教学效率;有助于教师关注教学的思维过程,加深对知识点的理解和巩固,提高备课的质量水平。思维导图备课是教学可视化新的选择。例如,《高等数学》中定积分的概念和性质时,制作思维导图如图3所示,由图可知重点是定积分的定义,难点是利用定积分定义计算定积分。
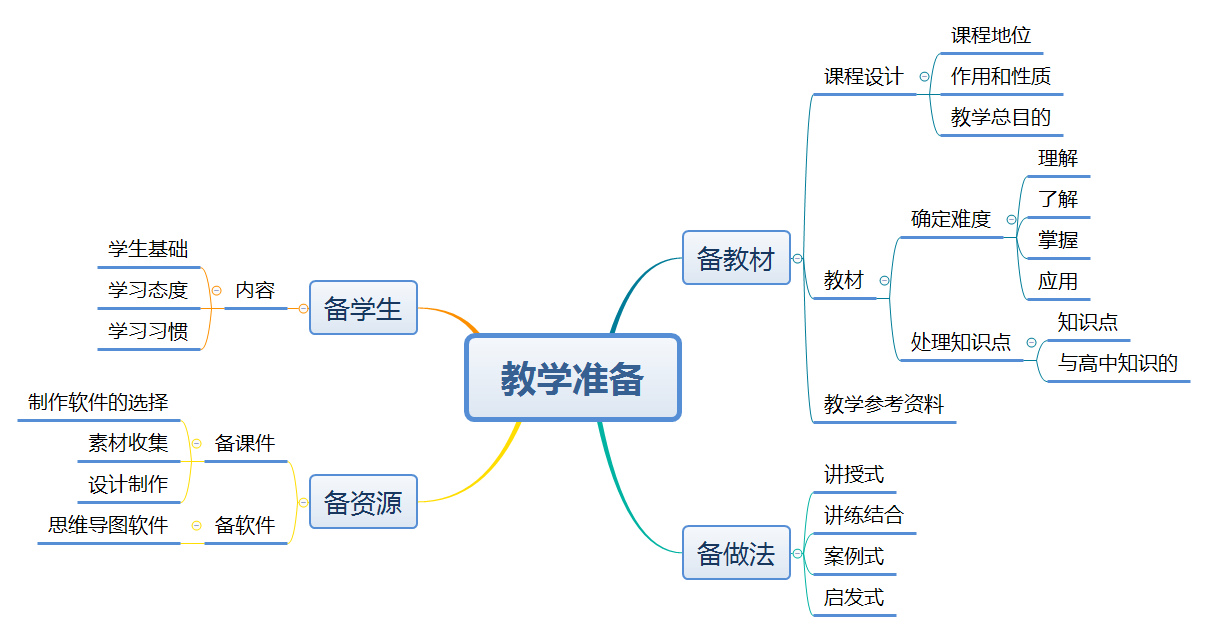
图2 教学准备思维导图
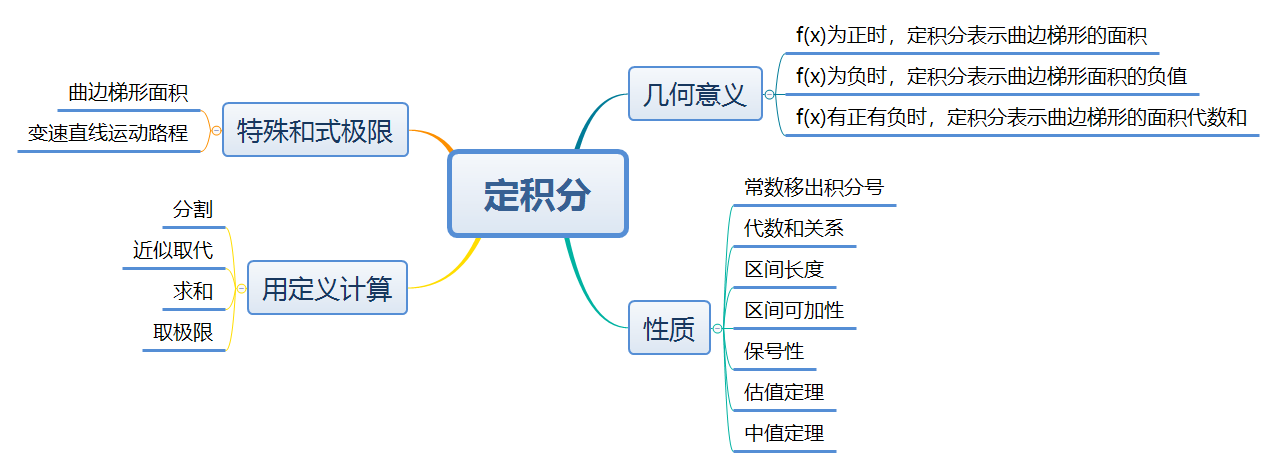
图3 定积分概念和性质思维导图
(3)思维导图在课堂教学中的应用,提高课堂教学内容的可视化
理工科专业课程理论性强、内容抽象客观、侧重推理和逻辑。课堂授课多数通过多媒体PPT辅助教学,然而PPT切换速度远超于学生的思维速度,学生课堂的注意力常常集中在幻灯片上的内容,很难把知识点融入到知识体系中。因此,教师课堂中借助思维导图板书,既可以使板书设计明确、主次分明、重点突出,也有利于学生从宏观上把握课堂重难点内容和时刻吸引学生的注意力[9]。以《高等数学》中未定式求极限的方法为例,制作课堂板书思维导图如图4。通过思维导图可以看出,和未定式求极限方法中的重点内容,其他的形式都需要转成和才可以使用洛必达法则。多媒体授课结合思维导图板书设计,突显出教学内容层次分明,重难点突出,有利于提升学生听课效率。
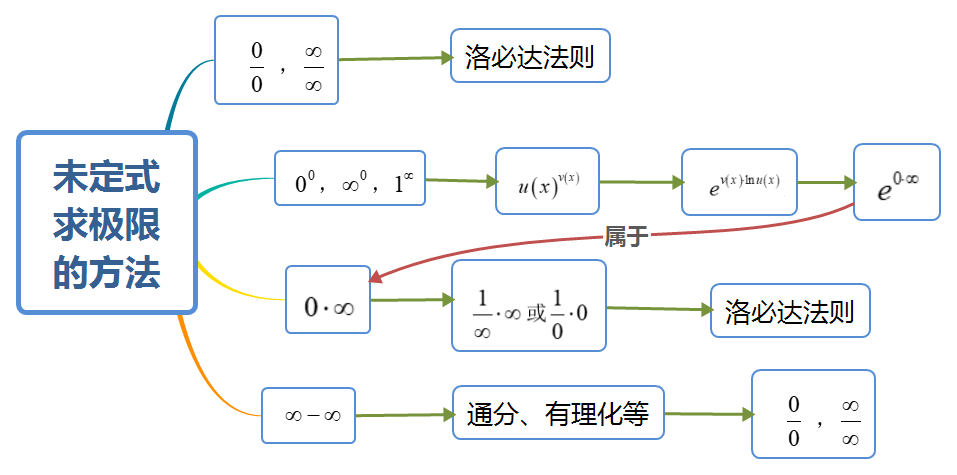
图4 板书—未定式求极限思维导图
(4)思维导图在解题时的应用,有助于理清解题思路[10]
理工科课程的学习中,通过解题形式充分理解、巩固和应用知识点,解题也是检验学生掌握重要知识点的关键环节。解题的过程中存在着一些普遍的规律和共同特征,一般由审题,建构、求解和验证这四个环节构成,如图5所示
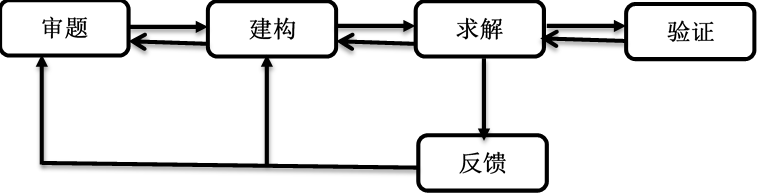
图5 解题过程示例图
通过思维导图解题,能够帮助学生在分析问题和解决问题的过程中更好的理清思路,以及注重引导学习者进行思维发散,例如解题思维导图如图6所示。
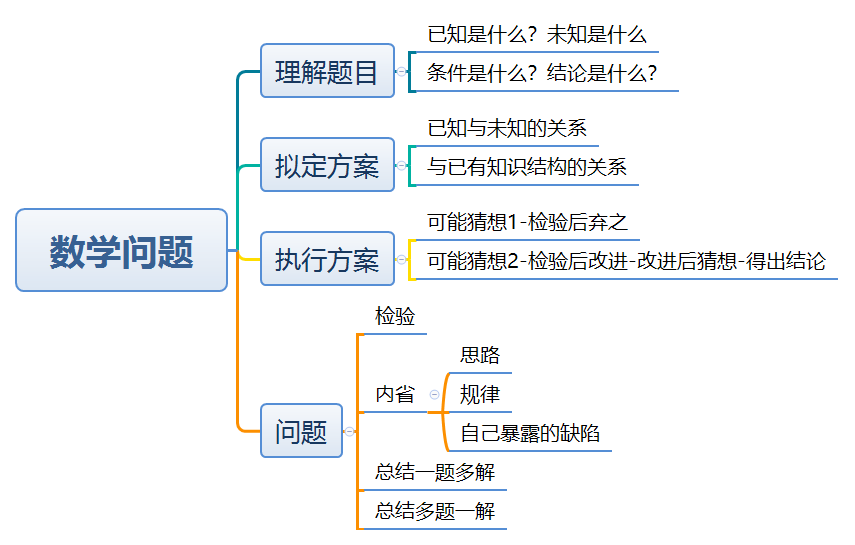
图6 解题思维导图示例
(5)思维导图在复习课中的应用,有助于学生提升归纳总结能力
复习课不是简单的重复知识点的认知,而是对知识的综合和升华,引导学生建立良好的认知结构,让学生把知识片段连结起来,形成逻辑严谨、层级分明的知识网络体系,充分调动学生的积极性和主动性,提升学生解决问题的能力和应用能力得到发展。然而思维导图不仅是一种思维工具,而且是一类总结工具。在复习课中使用思维导图,有利于学生对已学习的知识进行归纳结,有助于学生良好知识体系的形成,帮助学生系统和清晰的记忆知识,提升复习效果[11]。例如《高等数学》中不定积分章节复习思维导图[12]如图7所示,使得概念间的联系更加清晰,对积分方法的本质及方法的使用理解更加清晰。
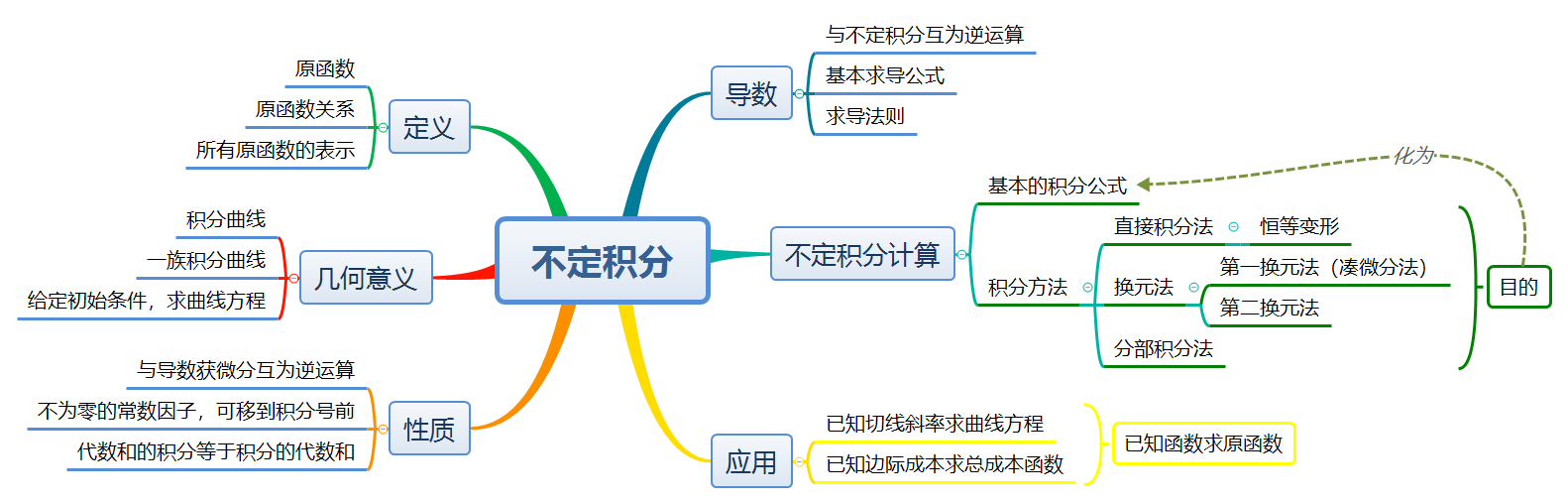
图7 不定积分思维导图
4. 思维导图在理工科教学中的意义
思维导图作为一种总结、发散思维的工具,通过图文并茂的方式将复杂的信息通过图形呈现出来,让复杂的问题变得简单化,已经在许多同行教学实践过程中体现出它的独到优势。结合教学实践,思维导图在理工科教学实践中的意义总结为以下几个方面:
4.1对教学理念的推进
课堂教学质量由教师的教学效果和学生的学习效率共同决定。将思维导图应用于理工科教学,教师由传统的知识灌输者转变为引导者:(1)利用思维导图的可视化特征,引导学生建立层次分明、条理清晰的系统化知识网络,体现了教与学的有机统一,有助于提升学生分析能力、整理知识点的速度;(2)利用思维导图中知识流动的多源性和交织性等,有效调动学生获取知识的主动性、积极性,提升学生分析问题、解决问题的能力[9]。综上,利用思维导图教学构建了学生自主构建知识的“输入”和“输出”,推进了课堂以“学生为中心”的教学理念。
4.2用于创新思维的培育
中共十八大召开以来,习近平总书记多次强调创新思维,指出:惟创新者进,惟创新者强,惟创新者胜。思维导图有利于培养学生的创新思维,主要是思维导图利用了与创造力相连的想象和联想技巧。思维导图的逻辑思维、发散思维和逆向思维三大特征,正是创新思维纵向思维法、横向思维法、逆向思维法的基本形式[13]。
(1) 逻辑思维是创新思维活动的前期的重要方面,既是激发灵感和创新活
动的基础,也是理工科思维的重要特征。思维导图应用于理工科教学,可将概念和公式组成一个网络知识系统,使学生清晰了解各个知识要素的本质特征和内在逻辑,有助于提升学生的逻辑思维能力。
(2) 发散思维是指不拘泥于已有的方式、方法,从多方面、多角度思考问
题。发散性思维关键在于联想,突破自我设限。思维导图的制作为理工科学生提供了一种从多角度思考问题的平台,从中不仅学会了知识的迁移,还有利于培养学生的发散思维。
(3)逆向思维是创新思维的一个重要方面,逆向思维是打破原有的思维方式,从逆向、相反的角度思考问题。运用思维导图进行学习时,思维导图的无限扩展性能够引导学生从相反的角度思考问题,因此学生的思维不会受到某种标准的约束。当理工科学生在解题时,从一种方式无法求解时,学生可以尝试从相反的方向寻找解题的方法,有利于逆向思维的培养。
5.结语
思维导图作为一类可视化的总结工具,结合它的发散思维和逻辑思维特征,应用于高等数学课程教学取得良好的教学效果。针对学生,思维导图不仅能帮助学生梳理分散的、零乱的知识点,强化知识点的记忆,而且通过思维导图的构建有助于提升学生分析问题、解决问题的能力,提高课堂教学效果和激发学生思维的发散性;针对教师,思维导图的应用有助于课前整体把握教学环节,理清教学思路;课中,利用思维导图的可视化特征板书,有助于突出教学重难点,吸引学生注意力,有利于推进高等数学教学改革。综上,思维导图作为一种辅助教学策略应用于教学中,进一步完善和提升教学效率,值得推广到其他学科。
参考文献
[1]许春根, 杨孝平, 赵培标,等. 加强高等数学课程建设提高人才培养质量[J]. 中国大学教学, 2009(4):43-45.
[2]闫湛. 运用思维导图优化高等数学学习方法[J]. 黑龙江科学, 2020, 11(21):13-15.
[3] 托尼巴赞.思维导图:放射性思维[M].李斯,译.北京:作家出版社,1998.
[4]杨凌. 概念图、思维导图的结合对教与学的辅助性研究[J]. 电化教育研究, 2006, 000(006):59-61.
[5]杨云霞, 郭英娃, 徐敏,等. 思维导图在结构化学课程教学中的应用与探索[J]. 化学教育(中英文), 2021, 43(10):46-51.
[6]莫芳芳, 马淑然, 王彤等. 将思维导图引入"中医学基础"教学的必要性[J].教育教学论坛,2021(03):125-128.
[7]韦丽兰. 思维导图在全科师范生微积分教学中的应用[J]. 数学学习与研究, 2021(16):2-4.
[8]施静. 思维导图在大学高等数学教学中的运用[J]. 数学学习与研究, 2018(23):18-18+20.
[9]闫勇,张丽红,刘靖靖,刘晓琦,胡青平.思维导图在微生物学教学中的应用实践[J].微生物学通报,2020,47(04):1019-1025.
[10] 张武威, 黄宇星. "思维导图"应用于"物理解题"的探究[J]. 电化教育研究, 2009(09):99-103.
[11] 吴志丹. 协作建构思维导图在数学复习课中的应用探究[J]. 电化教育研究, 2010(7):108-110.
[12]周巧娟. 概念图与思维导图在微积分教学中的融合应用[J]. 吉林省教育学院学报, 2019, 35(1):72-75.
[13] 刘慧茹、董晶、肖汉琼、金杰. 思维导图对医学生创新思维培养探析[J]. 中国继续医学教育, 2020, 12(25):67-70.
作者简介:
欧玉芹(1992-),女,广西北海人,硕士,助教,从事代数研究与数学教育研究
郑李玲(1978-),女,广西玉林人,硕士,副教授, 概率论与数理统计及数学教育研究
李智群(1979-),广西贵港人,硕士,副教授,从事最优化研究与代数研究;




