在高中阶段，大部分的学生已经对数学这门学科拥有了一定的认知，但由于高中阶段的数学知识相较于义务教育阶段，其深度和难度更大，学生在学习时很容易遇到难以解决的问题。教学中教师需要引导学生进行深度学习，同时，教师也需要更新教学理念，改变传统的教学模式和教学方法，在课堂中增添探究性学习活动，以便学生将知识内化。在深度学习的过程中，逐渐意识到学习数学的重要意义，体会数学知识的应用，从根本上挖掘数学知识的内涵，改善学生在课堂中的表现，促进学生学习效果的提升。
一 高中数学深度学习的特征
深度学习是与浅层学习相对的一种高效学习理念和学习方法，强调学生在学习中对知识的深度探究、理解和实践，高中数学深度学习主要具有以下几个特征：
第一，学生进行主动学习。传统教学模式下，学生多处于被动接受知识的状态，学习兴趣并未被充分激发，学习效果难以达到预期目标。在深度学习状态下，学生要主动探究知识内容，并通过分析新旧知识的内在关联，主动构建完善的知识体系。
第二，注重学习反思。深度学习本质上属于自主学习模式，强调在自主构建、自主分析、自主探索和自主反思中内化知识。在深度学习过程中，学生在自省、自查和自纠中养成良好的学习习惯。
第三，实践性较强。当前教育环境下比较注重学生关键能力的发展。通过深度学习能够促进学生对数学概念、内涵及原理的理解，学生能够积极运用建模思想、数学思维来解决实际问题，进而提高思维的灵活性，在实践中逐渐养成举一反三的学习习惯。
二、深度学习在高中数学教学中的应用策略
（一）深度思考，渗透数学建模思维
思考是深度学习的基础，深度思考有助于激活学生的高阶思维，为核心素养的培养创造契机。建模思维是指对现实问题进行数学抽象，运用数学语言描述问题，并采取数学策略构建模型，以解决现实问题。教师在深度思考的基础上，引导学生从数学的角度发现、分析、解决问题，渗透数学建模思维，可以促进学生的高阶思维发展。
例如，在高中数学《正弦函数、余弦函数的图像与性质》部分内容的教学过程中，教师可以围绕三角函数图像以及性质在图像交换中的应用，引发学生的深度思考，使他们掌握三角函数相关重点知识。首先，教师可以运用“五点法”带领学生描图，让学生找出图像“y=sinx、y=cosx”在[0，2]上的五个关键点坐标。然后，绘制正弦、余弦函数的图像，引发学生关于正弦曲线、余弦曲线的思考。此时渗透数学建模思维培养，要求学生结合三角函数分析图像特点，使之理解正弦函数图像是一条“波浪起伏”的连续光滑曲线，余弦函数图像与正弦函数图像形状相同。为了培养学生的核心素养，教师还可以要求学生思考通过变换函数“y=sinx，x∈[0，2π]”图像，得到函数“y=1+sinx，x∈[0，2π]”图像的可行性，由此启迪学生的高阶思维，使之能够在深度思考的同时，以建模的方式分析、解决问题，既能加深理论知识学习印象，也能为下一步学习做好准备。最后，教师要让学生画出下列两个函数“y=1+sinx，x∈[0，2π]”“y=cosx，x∈[0，2π]”的简图，意在培养学生的深度思考能力，使之逐步形成高阶思维。学生在揣摩问题条件的基础上，运用“五点法”绘图，由此发展自我建模思维，掌握运用函数知识解决实际问题的技能，透彻理解三角函数相关基础知识，为后续的高级知识学习作铺垫。
（二）深度训练，增强数学运算能力
深度学习活动能够促进学生学习效率和质量的提升，立足深度训练培养学生的数学运算能力，可以让学生掌握不同的运算技巧，促进核心素养发展。数学运算能力是在明确运算对象的基础上，根据法则解决数学问题的能力。教师可以从运算法则、方法、程序等角度入手，引导学生在不同形式的训练中进行演绎推理，使之在得到正确数学结果的同时，掌握数学运算技巧，进而增强数学运算能力。
例如，在高中数学《复数的加、减运算及其几何意义》部分内容的教学中，教师要把概念和运算融为一体，围绕“复数运算的意义”引导学生进行解题，以帮助学生理解相关运算法则。首先，教师可以将负数四则运算与平面向量的加、减法运算法则建立联系，让学生理解复数运算的几何意义。然后，教师假设任意两个复数z1=a+bi与z2=c+di(a.b.c.d∈R))，根据条件推出(a+bi)+(c+di)=(a+bi)+(c+bi)=（a+c）+（b+d）i。此时，教师要引导学生进行思维训练，要求学生根据条件z1.z2.z3∈c推导出z1+z2=z2+z1与(z1+z2)+z3=z1+(z2+z3)，让学生理解复数加法运算规律以及法则。接下来要训练学生的运算能力，引导学生求平面内两点之间的距离，使之在类比复数加法意义的基础上，推导出复数减法的几何意义，在顺利求解的基础上，增强数学运算能力。最后，在训练学生运算能力的基础上，教师要针对学生的不同运算水平提出建议，要求学生系统复习复数的加、减运算法则，遵循由简入繁原则进行训练，使学生能够在深度训练中，提升自我运算的正确率和效率。
（三）深度实践，强化逻辑推理意识
逻辑推理是从事实和命题出发，依据逻辑规则进行推导的思维过程，一般分为“从特殊至一般（归纳、类比）”与“从一般至特殊（演绎）”两种形式。立足数学深度实践活动，强化学生的逻辑推理意识，可以取得良好的核心素养培养成果。教师可以依据教学目标设计实践活动，指引学生在深度实践中运用所学数学知识解决问题，强化学生的逻辑推理意识。
例如，在高中数学《抛物线及其标准方程》部分内容的教学中，由于抛物线体现圆锥曲线的共性和个性，由此可以构建整章知识体系，教师要围绕抛物线定义和标准方程，重点引导学生探索“求标准方程的方法”，强化学生的逻辑推理意识。首先，教师可以介绍抛物线、抛物线焦点、抛物线准线概念，引出抛物线的标准方程y2=2px（p>0）。然后，带领学生运用抛物线的标准方程解决问题，选择建构不同的坐标系，得到不同形式的标准方程，要求学生根据标准方程y2=6x求出焦点坐标和准线方程，再根据焦点坐标F（0，-2）求出对应标准方程。如此一来，学生能够在深度实践中初步建构知识体系框架，在实践中进行演绎和推理，求出标准方程y2=2px（p>0）的焦点坐标（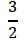
，0）和准线方程x=--
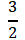。在此基础上，学生根据条件“焦点坐标F（0，-2）”进行分析，在实践中进行逻辑推理，得到“抛物线焦点在纵坐标轴的负半轴上”的结论，求出标准方程x2=-by。最后，教师要结合实际的“卫星天线接收信号”问题，引导学生运用所学知识，探索求抛物线标准方程、焦点坐标的方法。在深度实践中，教师引领学生分析具体问题，让学生绘图、推理、演绎，强化学生的逻辑推理意识，提升其实践素养。
三、结语
综上所述，要引导学生进行深度学习，教师需要不断改变教学模式，通过新颖、有趣的学习方法，应用生活化理念促进学生进行深度学习，利用信息技术优化深度学习环境，开展实践活动引发学生深度学习。希望本文能够为教育工作者提供一些帮助，使学生在深度学习、深度思考的过程中，实现优良的学习效果。
参考文献
[1]刘鹏．基于核心素养的高中数学深度学习研讨［J］．安徽教育科研，2022（36）
[2]吴玉章．指向深度学习的高中数学作业设计探讨［J］．中国数学教育，2022（24）
[3]杨子圣．高中数学教育重在培养数学能力与数学思想等核心素养［J］．人民教育，2022（23）
