温度控制系统普遍存在滞后性、时变性及非线性等动态特性^[1]，同时被控对象很难用精确的数学模型进行描述^[2]。而PID（Proportional Integral Derivative）控制作为工业领域中最常用的控制策略之一，广泛应用于温度、液位、压力、电机等控制过程。在传统PID控制基础上，逐步发展出了串级控制、Smith预估控制、神经网络控制的方法，有效弥补了稳态精度低、超调量过大等缺点^[3]。其中，神经网络本身强大的自学习能力，在PID控制方面得到了很好的效果。

1 传统PID模型

 PID控制原理图值与实际输出值构成偏差

                           （1）

传统PID控制的动态方程为

                  （2）

式中为误差信号，为比例系数，为积分系数，为微分系数。将公式（2）进行拉普拉斯变换，写成传递函数为

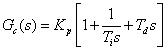                          （3）

2 BP神经网络的PID控制

在传统PID模型上，引入神经网络，将BP神经网络和增量式PID控制相结合，对DBF激光器进行建模^[4]，取得了令人满意的效果；用于无线分布式温度控制系统^[5]，在控制速度和控制精度上，满足了要求；在漆包线检测仪控制温度过程中，稳态误差较小，迅速达到了控制要求^[6]。

2.1 增量式PID算法及整定

增量式PID控制算法，如公式（4）所示：

  （4）

其中：t=0，1，2…… 表示不同时刻；为控制量，为偏差，为比例系数，为积分时间，为微分时间。考虑到所控制输出和控制目标为一一对应关系，故在本文温控系统的设计上，采用增量式PID控制。

对于增量式PID的调节，一般需对、和三个参数进行整定，传统的整定方法如依据技术人员的经验进行，一般情况下，依据比例-积分-微分的顺序，依次调整，费事费力；如依据响应曲面法进行，则需要根据表1的计算方法，对参数进行整定。

表1 响应曲线法的PID整定

2.2 BP神经网络

本系统采用的神经网络架构如图2所示。

图2 BP网络结构图

采用三层结构，输入层选取目标温度（SV），过程测量温度（PV），温度偏差e(t)；输出层为需要调节的三个参数、、；隐含层的确定根据公式（5）确定。

                               (5)

其中，n为输入层节点数，m为输出层节点数，a为取值范围[1-10]的常数^[7]。由于隐含层节点数的选取经常要根据实验来验证，如果模型过于复杂，需进行多次调整，经过综合考虑选取节点数为6。综上，本文选取3-6-3的神经网络结构。

再考虑到、、需为正数，故隐藏层的激活函数选取正负对称的S函数：

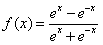                                (6)

系统的性能函数为：

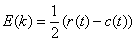                          （7） 

2.3 BP-PID模型

引入BP神经网络，构成BP-PID控制系统，如图3所示。

图3  BP-PID控制系统

与传统的PID调节相比，对三个参数、和的整定为自整定过程，即根据BP网络的特性，实时更新输入、输出和偏差，进而动态调节、、，满足系统的性能要求。

3 仿真验证

3.1 增量式PID仿真

设对象模型的传递函数用公式（8）表示。

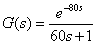                             （8）

采用传统的PID方法，需求得、、，用表1的计算方法可得：

借助MATLAB软件，用可视化工具Simulink设计PID控制模型，如图4所示。

图4  基于MATLAB的PID调节设计

根据上文的计算，把、、的计算结果输入模型，设输入信号为阶跃信号，幅值为1。运行仿真，仿真结果如图4所示。

图5 PID控制的单位阶跃响应图

3.2 基于BP-PID模型的设计及仿真

引入BP神经网络算法，完成、、的自整定。控制模型设计如图6所示。

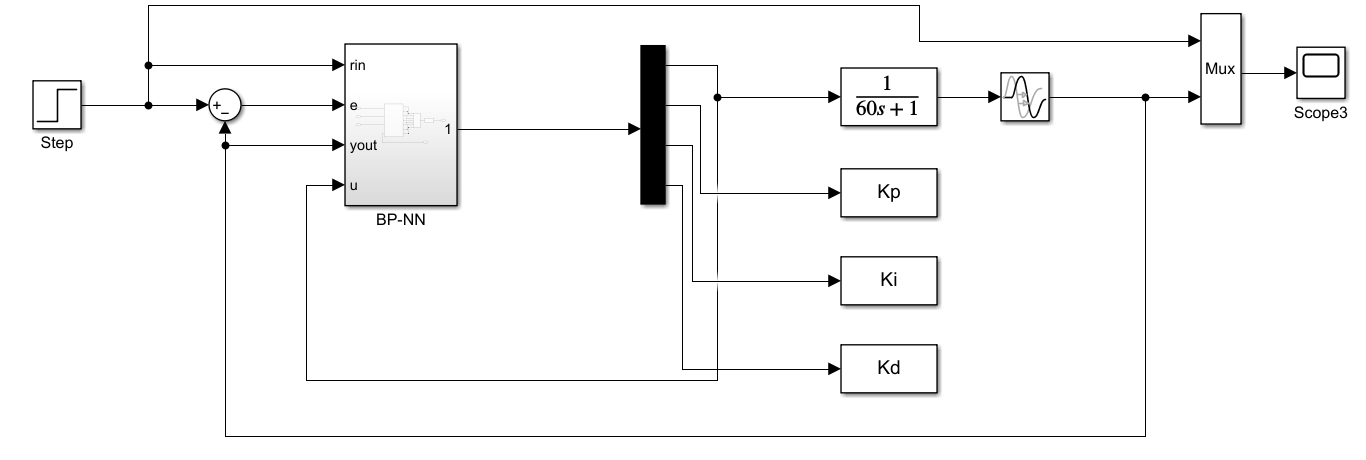
图6  基于BP-NN控制的PID调节设计

根据BP网络的算法，、、的整定过程在BP-NN的子系统内自动完成，设计思路为：

（1）网络结构为3-6-3结构，即输入层节点数为3，隐含层节点数为6，输出层节点数为3，动量因子取0.01，学习速率取0.2，；

（2）通过采样结果，计算设定值和实际值的误差；

（3）归一化处理；

（4）输出为三个参数、、；

（5）计算隐层和输出层的权系数。

仿真结果如图7所示。

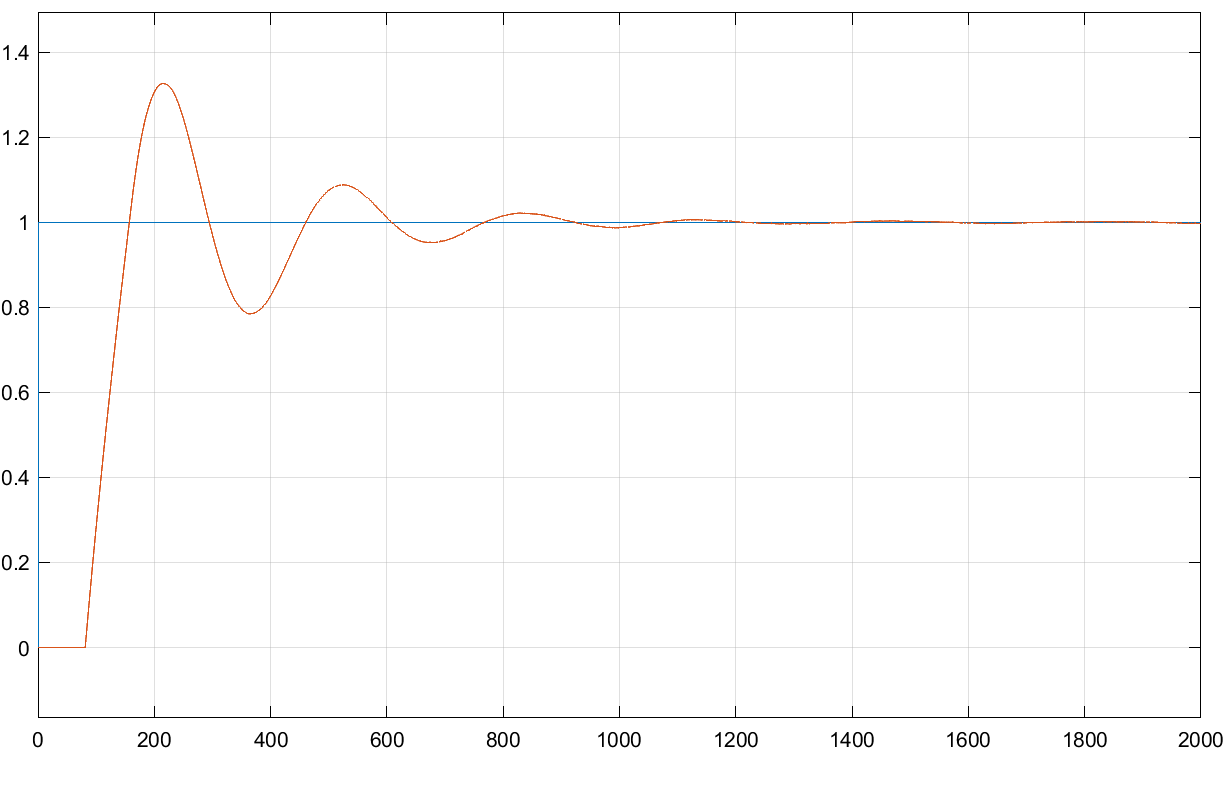
图7  基于BP-NN的PID控制单位阶跃响应图

4 结语

本文在传统的PID控制基础上，引入了神经网络算法改进PID控制，并通过MATLAB软件进行了仿真，结果表明，和传统PID算法，引用神经网络后，建立自整定的BP-NN模型，可自动调节参数，动态指标较好。

参考文献：

[1] 欧阳磊.基于自整定PID控制器的温度控制系统研究［D］.安徽:安徽理工大学,2009:5-8.

[2] 张皓,高瑜翔.前馈反馈Smith预估模糊PID组合温度控制算法[J].中国测试, 2020, 46(11):132−138.

[3] 赵景波,王众,廖鹏浩.基于粒子群优化算法的蒸汽温度控制研究[J].制造业自动化化,2020,42(06):107-111.

[4] 康伟.基于BP神经网络的DFB激光器恒温控制系统建模与仿真［J］.激光杂志,2015,36( 4) :59－61.

[5] 田波,周武能,周全权等.基于BP-PID算法的无线分布式温度控制系统[J].控制工程,2015,22(05):841-847.

[6] 雷翔霄,徐立娟.神经网络PID算法在漆包线检测仪中的应用[J].机床与液压,2020,48(19):104-107.

[7] 沈花玉,王兆霞,高成耀等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008(05):13-15.