引言：

废包壳清洗器具有较为广泛的应用前景，其工作原理主要是，将物料颗粒通过清洗器顶端加入，使其在底部螺旋滑道上产生堆积，其中清洗器的液位具有一定高度，物料通常可以在浸泡一段时间后，通过动力装置的开启，使其开展规律性的周期转动，即正向旋转，迅速反向旋转以及静止。通过依靠清洗器产生的惯性，推动物料颗粒向上运动，在清洗过程中需要使液体进行一定时间的停留，随后通过清洗器顶部排出。

一、废包壳清洗设备的计算流程与方案

在对工况进行明确的前提下，如果需要对废包壳清洗器进行直接仿真，具有较大的计算量，同时会造成大量时间的损耗。造成该问题的主要原因是，首先清洗器具有较大的尺寸，在转筒内部进行计算域需要进行大量网格计算，才能实现对气液固三相流场的准确模拟。其次，进行一次废包壳清洗的时间较长，达到了160分钟，在其中离散元模拟物料的运动耦合时间为10-4秒量级，具有较高的迭代计算成本。最后，需要进行清洗的物料中包含较多的颗粒物质，具有极大的计算量。从以上分析出发，在清洗设备的实施过程中，可以对一下方面进行简化。第一，选择清洗器结构的一部分开展仿真，推动计算效率的提升。第二，可以在保留清洗器几何特点的前提下，对清洗器的内部计算域进行适当的简化。第三，可以借助铺满底层滑道的颗粒量进行仿真，从而减少计算量。第四，对扁管的形状进行近似处理，从而更好的解决运动出现的穿模问题。第五，可以对物料清洗过程的周期性规律进行把控，对颗粒在清洗器中的运动情况进行模拟。通过以上模拟活动的开展，可以大幅度减少时间成本。

基于以上分析的开展，本项目从清洗器几何体以及颗粒量简化的基础上，对颗粒的运动规律进行模拟，从而对清洗器的结构以及具体的操作工况进行优化计算，具体方案如下。

（1）对颗粒量进行改变，开展对比计算活动，从而验证颗粒量简化计算的合理性。

（2）在简化的清洗器几何结构中，可以在制定的工况下，进行颗粒运动规律模拟，从而分析得出颗粒在清洗器运动过程中展现出来的运动特点。

（3）可以从已经构建的模型上，在给定的清洗器几何结构中，对比无水以及有水环境下，清洗器内颗粒运动发生的差异，从而得到水惯性产生的影响。

（4）可以在对清洗器的局部结构进行了解，通过颗粒量的简化，对转速，滑道坡度以及台阶高度进行对比计算，从而在分析相关条件对颗粒爬升效率产生的影响，从而更好的对清洗器内部结构与操作工况进行优化设计。

二、废包壳清洗器设备的仿真计算方法

（一）有限差分法

在数值的计算活动中有限差分法属于最经典的方法，其将求解的区域进行划分，设置差分网格，通过有限网格节点的应用，代替连续求解域，之后借助偏微分方程的导数进行差商替代，从而得出相应的差分方程组。在对方程组进行求解时，实际是微分方程定解问题的数值近似解，这属于一种将微分问题转变为代数问题的近似数值解法，该方法得到了长期的发展，逐渐成熟，大多应用于求解双曲型以及抛物型问题。

（二）有限元法

有限元法是通过一个连续的求解域进行任意的划分活动，使其划分为适当形状的微小单元，并在各个小单元内容构建插值函数，并依据极值原理，将问题的控制方程进行转化，使其成为所有单元上的有限元方程，将总体极值作为各个单元的极值和，即局部单元的总体合成，逐渐融入到指定边界条件的代数方程组中，对方程组进行求解，从而得出各个节点的待求函数值。有限元法计算的基础是极值原理以及划分插值，其吸收了有限差分法中进行离散处理的内核，同时借助变分计算的方法，更加贴近函数，并对区域进行积分计算，属于两种方法的相互结合，该方法适用于几何以及物理边界较为复杂的情况，有助于程序的标准化。

（三）有限体积法

有限体积法是对计算区域进行网格划分，使每一个网格的周围涉及到互不重复的控制体积，可以将待解的微分方程对每一个控制积分进行收集，从而得出一组离散方程。从选取积分区域的角度来看，有限体积法属于加权余量法中的子域法。可以从未知解的近似方法出发，有限体积法是采取局部近似的离散方法，其中涉及到的思想更容易理解，可以直接得出物理解释，其中离散方程的物理意义，指的是因变量在有限大小的控制体积中遵循的守恒原理，如微积分方程表示因变量在无限小的控制体积中的守恒原理。

三、废包壳清洗器过程的结果与影响

废包壳清洗器内的颗粒爬升效率受到几何机构参数以及操作工况的影响，本文对清洗器的结构进行分析，通过其结构的优化，可以使颗粒在规定时间内排出清洗器液面。可以将颗粒量作为定值，对影响的因素进行对比计算活动。

（一）转速影响

将螺旋滑道的坡度以及台阶高度作为恒定内容，对清洗器在不同转速条件下，颗粒的爬升规律，并加以总结归纳。其中颗粒爬升的动力主要来自于清洗器的转动以及其中水的惯性，转速会直接影响到水的惯性大小。可以在5个转动周期内，设置不同的转速条件，明确中心截面的流场分布。在相同的几何参数条件下，正转、反转以及低转存在明显的差异。三种不同工况导致正视图中心截面的速度分布云图存在差异。在相同的清洗器结构参数下，不同转速形成的速度分布具有较大差异，低转速与高转速条件下产生的流场虽然在量级上存在差异，但其实际分布具有一定的相似性，可以在清洗器上形成较高速区域，在截面的中心底部出现火焰状的低速区域，造成这些现象的原因是近壁处与中心区域遭受的离心力不同，其中距离旋转轴较远的近壁处具有更大的加速度。另外，在高转速的影响下，清洗器中心的低速区域呈现出明显的减少态势。而在中速条件下，低速区域主要集中在截面的中部。由于颗粒受到离心力的作用，逐渐汇聚在螺旋滑道靠近转筒壁面的区域，在近壁区形成了范围较大的高速区域，通过水的惯性作用，带动颗粒爬升。这时，中、低、高速表现出的平均速度明显不同，表明了清洗器的流场速度并不是随着转速的升高而增长的，究其原因是清洗器的运动周期包括正转与反转。不同的计算工况下正转与反转的加速度呈现出同步增大或缩减的形式，高转速条件下产生的反转消耗的动能随着增大，因而转筒内的平均速度是伴随着转速的增加首先呈现出降低，之后升高的趋势。为了确定清洗器的最优转速，可以避开中等转速范畴，选择合适的近壁区为高转速的实现提供条件。其中转速的流场分布如图1。

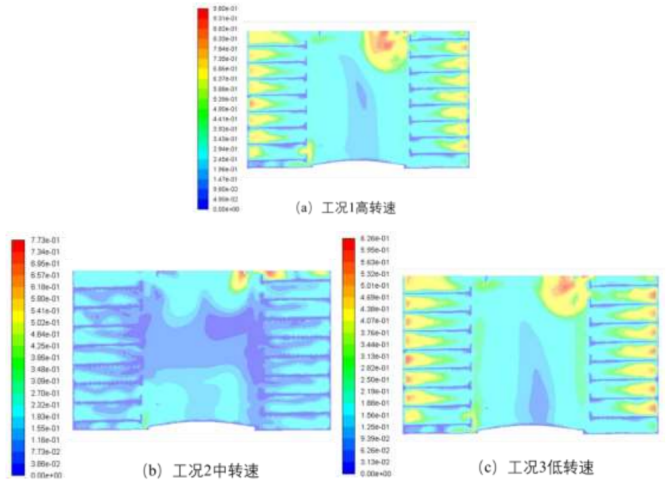
图1 不同转速下的流场分布

根据转速条件的不同，颗粒的爬升效果存在明显的差异。其中在低转速条件下通过5个周期，颗粒仅爬升到第二层的螺旋滑道左侧，在中转速条件下，颗粒爬升到第二次螺旋滑道的右侧，并进入第三次滑道，高转速条件下的差异更加明显，颗粒爬升到第四层滑道。根据以上仿真可以得出，颗粒爬升速度与清洗器的转速成正比，随着转速的增加，颗粒与水之间的相对速度增加，同时提高了拉到颗粒爬升的曳力。其中不同转速下的曳力如图2。

图2 不同转速下的曳力

在不同的转速条件下，颗粒的平均速度以及距参考点的距离存在明显的不同。根据实际的实验结果，可以发现三种转速条件下，颗粒的平均速度随时间的变化趋势较为相似，通常在第二周期后呈现出稳定增长态势。在中等转速基础上增大25%形成了极为明显的差异，如果是降低25%，那么颗粒速度的变化与中等转速的差异较小。颗粒到原点的距离变化在高转速条件下的爬升效率明显高于中速以及低速情况。总之，在以上三种转速情况下，颗粒到参考点的距离会伴随着时间呈现出增大的趋势。其中不同转速下的颗粒平均运动速度大小变化如图3。

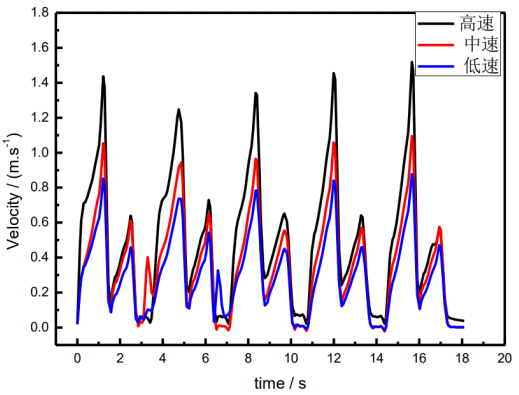
图3 不同转速下的颗粒平均运动速度大小变化

（二）清洗结果

在确定的操作工况下，可以对清洗的结果进行分析，发现第二个转动周期处于正转的加速末期，实际的转速很难达到预期效果，其中正向中心截面的速度左侧已经转过的区域相较于右侧区域高。在正向逆时针加速转动的条件下，左侧螺旋滑道上的液体具有具有较快的速度，其加速效果明显，另外，中心区域的速度分布不均，实际的流动速度较为迟缓。在实验的过程中，内圈物料与外圈物料运行缓慢的现象相吻合。通过了5个转动周期的运转，气液混合物的速度逐渐稳定，这时清洗器的上层空气基本处于静止状态，少量的液体会飞溅到上部区域，与现场的实际操作情况相契合。另外，通过了5个周期的正反交替转动，滑道上的高速区域并不局限在清洗器的左侧，而是分布于清洗器两侧，中心部分的速度分布具有较强的均匀性，并逐渐朝向区域稳定发展。其中涉及到废包壳、扁管以及碎屑物料的模拟数据分析活动，并得出转筒内的颗粒运动规律。在初始状态下，颗粒会通过清洗器的顶端排料口进入，并逐渐落入水中，在底部的水平螺旋滑道上产生堆积。在形成的初始堆积结构中，由于下落过程中颗粒之间以及颗粒与滑道产生的碰撞，少数颗粒会直接从底部进入到第二甚至第三层滑道。其中桶内的速度分布如图4。

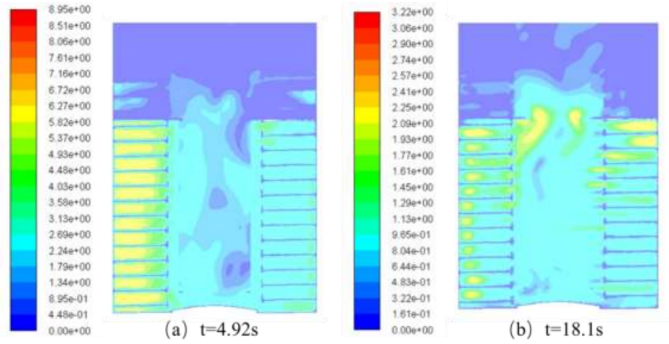图4 不同时刻清洗筒内的速度分布云图

废包壳清洗器底部具有一个圆锥形的凸台，并且最底层的滑道相较于第一层的螺旋滑道具有更大的宽度，可以使落下的颗粒在接触到圆锥后顺着锥面下滑，并最终部分落到底部的水平滑道上，部分停留在转筒底部的中心区域。在完成一段时间的浸泡后，可以通过清洗器的启动，使颗粒逐步从底部中心区域运送到螺旋滑道上，并得出物料在转动周期内的速度与位置变化规律。在经过正转0.4s后，受到离心力的作用，逐渐朝向螺旋滑道的边缘聚集。之后，在反转产生的巨大惯性的作用下，各个区域内的颗粒得到集中。在反转结束后，正转与反转的间隔时间内，转筒中的水并不会立即静止，并且以及聚集的物料经过水的冲刷，会沿着滑道运动，受到冲散，其中滚动能力更强的扁管可以随水运动更长的距离，并提高爬升速度。总之，在清洗器的周期性转动下，物料颗粒处于稳步爬升状态，具有十分明显的位置变化。

在简化颗粒数量条件之下的颗粒往往堆积在一侧的重要原因为：当颗粒的数量不足时，其稀薄的地方覆盖的位置为清洗器的底部，而颗粒之间并不是完全连续，而是存在空白区，从而让曳力推动颗粒，使其在上升时无法连续不断来带动物料颗粒向上运动，当到达间断位置时没有能够拖动其上升的颗粒，从而形成了颗粒带积压在一侧，且呈现出间断状态。简化颗粒数量条件之下的颗粒积压往往处于小半个圆面之内，其在未简化的时候，在整个的圆面之内都是有分布的。其颗粒在向上运动的时候，无法仅依靠转筒的正、反转这一惯性，实际上，水的影响也至关重要。如果分布的加料量、转动条件相同，在计算无水、有水的时候物料颗粒存在运动特性方面的差异。如果在无水情况下转动的五个周期，颗粒于转筒内的具体的位置分布，把扁管进行标记，可标记的颜色为粉红色，如果没有水的惯性作用，t=18.1s的时候扁管实际上大部分刚刚运动到的位置为第三层螺旋滑道，且该扁管在挨着筒壁的位置才呈现出具有一定规律的分布。这和实际操作时扁管如果处于无水情况，其在空气当中的爬升排布规律并不冲突，是一致的，实际上，其所使用的设备在运行的时候，扁管也挨着筒壁进行排布，说明计算存在一定准确度。其中不同周期内颗粒距参考点的变化如图5。

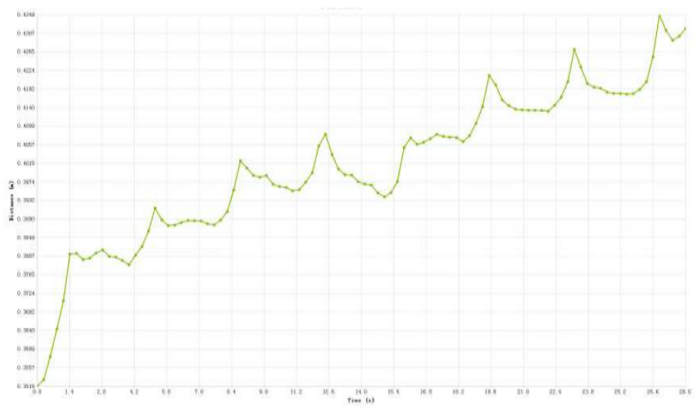
图5 不同周期内颗粒距参考点平均距离随时间的变化趋势

四、结束语

综上所述，在对转速以及结构条件进行明确的前提下，物料颗粒在不同周期内呈现出的运动规律为，正转时在滑道上进行有序分布，之后通过离心力的作用，慢慢聚集到转筒边壁附近，并在反转的周期内实现进一步聚集。随后在正反转的间隔时间内，在水的惯性冲击下，冲散集聚的颗粒，并散落分布子啊各个小区域内，中心区域的速度缺乏均匀性，实际的流动速度较慢。以上活动与内圈、外圈的物料运行现象相吻合。在颗粒沿着螺旋滑道进行爬升时，不仅依靠了转筒的惯性，同时依靠水的惯性。在有水的情况下，颗粒的爬升速度得到了较为明确的提供。在实际的清洗器优化过程中，可以通过转速更好的利用水的惯性，推动颗粒爬升效率的提高，并伴随着转速的增大而增大。

参考文献：

[1]邵婕文,柏磊,王晶.γ能谱法测量分析废包壳中铀和钚含量技术研究[J].原子能科学技术,2023,57(05):1032-1039.

[2]王丽莎,孙明波,王静等.废包壳倾倒装置制造难点剖析[J].中国核电,2022,15(04):576-579.

[3]汪世军,刘运陶,张春龙等.一种废包壳监测系统及其应用分析[J].核电子学与探测技术,2022,42(04):652-656.

[4]马鸿宾,郭鑫宇,武毓勇等.压水堆乏燃料后处理厂的废包壳特征研究[J].广东化工,2022,49(08):133-135.

[5]柏磊,王仲奇,刘晓琳等.乏燃料棒中关键核素径向分布特点及对废包壳测量准确度影响[J].原子能科学技术,2020,54(05):888-894.