如今能大部分的原油都是利用长输管道进行输送的,不过我国80%以上的原油都是含蜡原油,其温度大于原油凝点,所以极易发生各种事故,严重威胁含蜡原油管道的安全,为有效减少事故发生,就引用了新的停输再启动压力计算方法,经过最小启动压力以及泵加压性能判断管道是否能够再启动。不过含蜡原油流变性导致的非牛顿流体非稳态流动非常复杂,使得原油管道再启动的水力计算就变得极其难,并且停输温降的计算误差还会严重影响水力计算,所以国内外很多学者都开始对停输再启动过程展开研究,国外主要研究了首站恒压水平管道,我国主要研究了牛顿体与非牛顿体管道启动压力,含蜡原油再启动压力计算方法是在启动压力的基础上实施优化的。
一、停输再启动压力计算模型
基于管道首末的高程差影响,就运用了区域离散化方法计算平衡摩阻,同时利用能够反应原油触变性的Houska触变模型来算出剪切应力。停输再启动压力的公式为:p=pg+pa+pl。其中,p表示停输再启动压力;pg表示高程压降;pa表示惯性压降;pl表示摩阻压降。对于高程压降来说,其公式如下所示:pg=ρgl·sinα。其中,l表示管长;α表示管道的倾角。对于惯性压降来说,其能够让流体产生加速度,从而由静止变为带有流速的压力,其和传统模型的水平管道类似,所以能够通过动量方程得出。虽然长输管道启动时,管里的原油会按照从前向后的顺序启动,但是受首站泵压的影响,会产生很大的压力波,从首站传到末站,并且压力波是不断变化的,这样每列压力波导致的流量增量ΔQi就会不一样,所以需要计算出惯性压降每列压力波的传播时间以及每个时刻的位置,其公式如下所示:
pi=ρ·U·α·4·ΔQi·ρ·α/(π·D2)。其中,ΔQi代表第i列的压力波流量增量;D代表管道的平均内径;ρ代表原油的密度;α代表压力波的传递速度。压力波可通过软件SPS得到。对于摩阻压降来说,其包括两部分:平衡摩阻压降和触变性压降。通常摩阻压降会产生克服流体和管壁之间摩擦阻力压力,并且产生破坏原油结构的屈服力,因为触变性导致的压降会随着剪切时间增加而增大,所以触变性启动压力必须考虑触变性摩阻压降。由于传统模型的油温和剪切速率都是假设不变的,运用指数函数计算原油触变性不准确,而且利用牛顿体稳态流动公式计算剪切速率也不满足要求。模型的设置是以管道沿线温度场分布情况进行的,对温度进行分段,然后把各段的压降进行迭加,再对管道实施区域离散化处理,利用有限个离散点替代连续的空间,这样每一个子区域的节点就代表每个控制容积,最后计算节点,由上一个泵站出口开始至下一个泵站进口结束。再启动平衡摩阻压降的公式如下所示:p1l=4∑Li·τi/Di。其中,τi代表第i段离散管道节点处原油的平衡剪切应力;
Li代表第i段的管道长;Di代表第i段管道内径。触变性压降的计算公式和平衡摩阻计算公式基本一样,剪切应力可通过Houska触变模型得到。触变模型的主要思路就是通过结构参数体现物料某状态下的结构情况。模型于剪切过程既具有结构建立,又具有破坏,该破坏主要是屈服应力与稠度等速裂解。因为Houska触变模型的参数和温度没有关注,所以只考虑时间变化,剪切应力的计算公式如下:τw=τy0+λ·τy1+(K+λ·ΔK)·
rn。其中,τw代表剪切应力;τy0代表结构良好裂解下的屈服应力;τy1 代表结构建立下的屈服应力;K代表稠度系数;ΔK代表触变性稠度系数;r代表剪切速率;λ代表结构参数,于0-1取值;n为常数。
二、实例检验情况
为有效验证计算方法的准确程度,在此选取某输油管道进行检验,该输油管道承担着原油输送的重要任务,其管道总共长349.19km,管道直径为529×7mm,埋深为1.5m,设计压力为4.5MPa,输量为750×104t/a,整个线路总共有6座热泵站。利用新的再启动压力计算模型编辑系统能够计算出停输再启动压力,在此计算了两个时间点的停输再启动压力,分别为时点1和时点2,详见表1、表2所示。管道输送含蜡原油Houska触变模型的参数都是通过实验数据拟合获得,详见表3所示。
表1 时点1管道各站间运行工况均值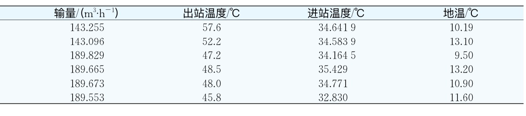
表2 时点2管道各站间运行工况均值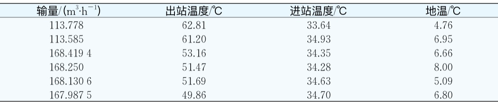
表3 含蜡原油Houska触变模型参数
利用上述数据能够算出时点2输油管道停输12h以后各站的再启动压力。因为最小启动压力是管道将要启动时临界的压力,启动波速约为0,惯性压降可忽略,所以结果都不考虑惯性压降。同时还能计算出时点1输油管道12h和14h各站的停输再启动压力。通过研究能够发现于相同工况下,停输的时间越长,再启动压力就越大,造成该现象的主要原因是因为停输时间会影响停输的温度场分布情况,而温度场分布又会影响含蜡原油的触变性,最终使得平衡摩阻压降与触变性压降均产生改变。
三、总结
通过上述内容可知含蜡原油管道停输再启动压力的主要特征,经过对传统启动压力模型的不断优化和改善,目前压降主要包括三种情况,分别为:高程引起压降、惯性压降以及摩阻压降,其中摩阻压降主要是因为触变性导致的,其可利用区域离散化计算摩阻压降,再运用适合含蜡原油触变性的Houska触变模型进行计算,含蜡原油停输再启动的计算结果与实际非常符合,经过编辑计算程序就能有效增强计算效率,通过模型计算程序能够有效计算再启动压力。为验证计算的准确性,还特意将某输油管道的历年数据导入含蜡原油管道停输再启动压力计算模型当中,其结果和实际一样,说明再启动压力计算方法非常可靠、准确。
参考文献
[1] 王兵,李长俊,邓青,等. 热油管道停输后再启动数值模拟[J]. 石油天然气学报(汉江石油学院学报),2007,29(6):476-478.
[2] 蒋新国,刘爱虢,丁启敏. 热油管道停输再启动过程[J]. 天然气与石油,2005,23(2):25-27.
[3] 郝迎鹏,张国忠,刘刚. 胶凝原油管道再启动相关问题研究现状[J]. 油气储运,2013,32(7):685-691.
[4] 李明忠,刘陈伟,李家院,等. 深水油气管道再启动过程模拟计算[J]. 油气储运,2012,31(7):525-529.
[5] 刘天佑,高艳清,曹强,等. 原油长输管道启动压力研究[J]. 油气储运,1997,16(12):7-13.
[6] 李才,张晓萍,苏仲勋,等. 热含蜡原油管道停输再启动压力研究[J]. 油气储运,1998,17(1):10-14.










