引言
近几年来交通事故数量所造成的死亡人数虽然有明显下降，2018、2019年因交通事故造成的死亡人数为6.3万人[1]，交通事故数量所造成的死亡人数基数大，安全形势仍不乐观，有必要对交通事故死亡人数进行预测，交通事故预测属于复杂的非线性预测问题，它是交通安全设计的基础。对于道路交通事故的合理预测可以有利于掌握交通事故的未来状况，合理评价交通安全措施的可行性和实施效果，对各影响因素有效地控制，从而达到减少交通事故的目的。文献[2-3]提出了灰色GM（1，1）预测模型，但灰色GM(1,1)预测模型仅仅从历史数据建立函数关系，依赖于历史数据规律特征，从而造成预测误差大。文献[4-5]提出了BP神经网络预测模型，BP神经网络建立多层输入输出的非线性映射关系，预测效果相对较好，故本文采用BP神经网络预测交通事故死亡人数，该预测方法、结果为交通部门管理工作提供参考，实现交通事故向预防性转变。
1交通事故影响因素及相关性分析
相关文献[6-8]认为道路交通事故主要有如下一些影响因素：人口数、人口密度、人口事故死亡率、机动车密度、公路客运量、公路客运周转量、公路货运量、公路货运周转量、民用车拥有量、万辆机动车事故死亡率、10万辆自行车事故死亡率、路网密度、道路等级、质量、线形标准等、人均GDP、GDP增长率等。
为了使选取的道路交通事故影响指标更加可靠，本文首先对初步确定的交通事故影响因素与交通事故死亡人数进行相关性分析，选取相关系数较大的影响因素作为影响指标，再根据选取的影响指标确定交通事故的预测目标，即预测指标。若选取的影响指标与预测指标关系不大或者不相关，不但会增加计算的工作量，还会影响预测结果的准确性；因此，在选取预测指标时，需先进行相关性分析。将选取的各个影响因素与各个预测指标分别进行相关性分析，选取相关性大的作为影响指标。
查阅中国国家统计局数据库1998-2019年的GDP、人口数、机动车驾驶人数、公路里程、公路客运量、公路旅客周转量、交通死亡人数等数据，见附件表1所示。利用SPSS数据分析软件对GDP、人口数、机动车驾驶人数、公路里程、公路客运量、公路旅客周转量、公路货运量公路、货运周转量分别与交通死亡人数进行相关性分析，见表2所示。
表2 交通事故死亡人数影响因素相关性分析
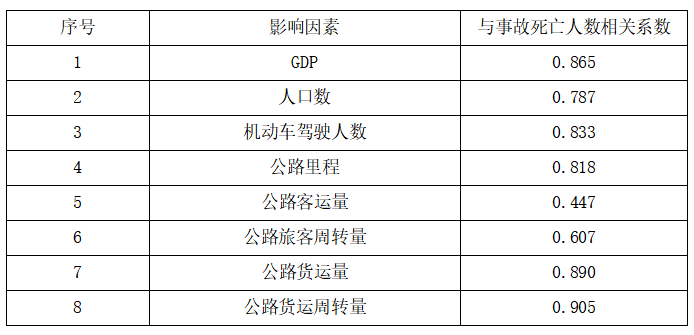
在进行交通事故死亡人数预测时，将相关系数低于0.6的影响因素舍掉，将GDP、人口数、机动车驾驶人数、公路里程、公路旅客周转量、公路货运量、公路货运周转量作为BP神经网络输入层。
2算法原理
2.1 GM（1，1）原理
GM（1，1）是一阶的单变量的灰色预报模型，它可以利用少量的数据建模，对数据序列的变化规律进行预测。由于交通事故数量及死亡人数的变化规律不易掌握，因此可以用GM（1，1）对其预测。
设原始数据序列为
，经过一次累加生成的新序列为：
（1）式（1）中，
求累加序列
的均值数列：
（2）则
对累加序列
建立灰微分方程：
（3）相应的白化微分方程为：
（4）其中a称为发展系数，b称为灰作用量[9]。
令
， 
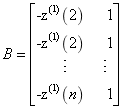则 GM（1，1）
模型可以表示为矩阵方程：（5）通过最小二乘法可得到参数a、b的最小二乘解[9]：
（6）由此可得微分方程的解为：
（7）对上述解进行差分处理即得原始序列的预报值，即
（8）2.2 BP神经网络
BP（back propagation）神经网络是一种基于误差反向传播算法训练的多层前馈神经网络，它利用非线性基函数的线性组合实现从输入空间到输出空间的非线性转换，可以通过训练去逼近任意的非线性映射，对非线性时间序列预测问题有着较优的处理能力。BP神经网络由输入层、一个或多个隐含层和输出层构成，每一层都含有多个神经元，各层之间的神经元互相连接，同一层中的神经元彼此不相连，其基本网络结构如图1所示。
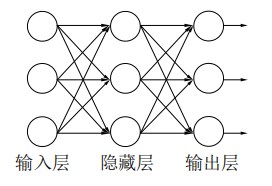
图1 BP神经网络基本结构
BP神经网络的基本单位为神经元，每个神经元将前一层神经元的输出作为输入，通过激活函数后输出。其中隐含层神经元一般用对数双曲函数或正切双曲函数等非线性函数作为激活函数，从而实现从输入到输出的非线性映射。各神经元之间的连接对应着一个权值，神经元的输入值分别与各自对应的权值相乘后求和，并加上神经元本身的偏置值后作为激活函数的输入，并得到相应的输出。BP神经网络训练的实质是利用误差反向传播算法修改各个权值和偏置值，使网络收敛[10]。
反向传播算法的具体实现过程如下：
1）为网络的各个权值和偏置随机赋初值，确定激活函数。
2）输入训练样本，根据公式求出网络各层的输出Z：
（9）式（9）中：Z为神经网络各层的实际输出向量，W为权值矩阵，X为输入向量，B为偏置向量，σ为激活函数。
3）根据误差函数公式，求出系统的性能误差：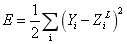
（10）式（10）中： 
为输出层第i个神经元的期望输出值，
为输出层第i个神经元的实际输出值。
4）求各层的误差
，对于输出层的误差
，有：
（11）式（11）中： 
为矩阵的哈达玛积运算符，
、
和 
分别为最后一层的权值矩阵、输入向量和偏置向量。对于其他层的误差
，有：
（12）式（12）中：l为当前层，l+1为后一层。
5）调整权值和偏置：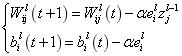
（13）式（13）中：α为学习速率，即步长，一般选取0.01～0.8之间的常数。
6）重复执行过程2）至过程5），直至系统性能误差降到预设值或训练次数达到预设次数，结束训练。训练完成的BP神经网络即可用来数据预测。
3预测结果分析
通过MATLAB对上述模型进行编程，利用GM（1，1）模型、BP神经网络模型分别对1998-2017年交通事故死亡人数进行拟合、训练，结果见表3所示。
表3 交通死亡人数拟合、训练结果
由表3可得，GM（1，1）、BP神经网络模型分别对1998-2017年交通事故死亡人数进行拟合、训练的平均误差为9.22%，1.95%；对比效果见图2所示。
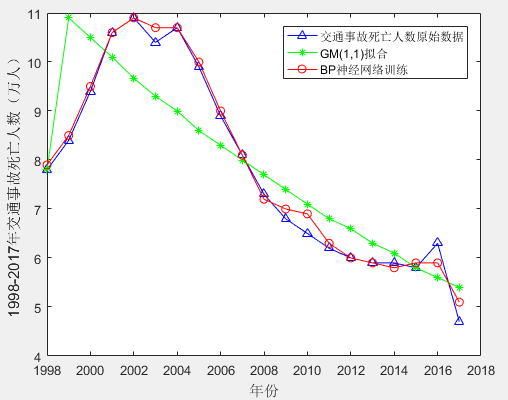
图2 GM（1，1）、BP神经网络模型拟合、训练对比效果图
利用GM（1，1）、BP神经网络分别预测2018-2019年交通事故死亡人数见表4所示。
表4 2018-2019交通死亡人数预测结果
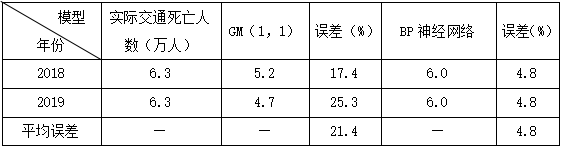
由表4可知，GM（1，1）预测2018-2019年交通事故死亡人数分别为5.2、4.7万人，BP神经网络预测2018-2019年交通事故死亡人数皆为6.0万人，GM（1，1）、BP神经网络预测2018-2019年交通事故死亡人数平均误差分别为21.4%、4.8%，说明BP神经网络预测结果更为准确。
4结论
本文进行交通事故影响因素分析、利用SPSS软件将交通事故影响因素与交通事故死亡人数进行相关性分析，筛选出相关系数为0.6以上的影响指标为GDP、人口数、机动车驾驶人数、公路里程、公路旅客周转量、公路货运量、公路货运周转量，影响指标作为神经网络的输入层，利用GM（1，1）、BP神经网络分别对交通事故死亡人数进行了预测，GM（1，1）、BP神经网络预测2018-2019年交通事故死亡人数平均误差分别为21.4%、4.8%，说明BP神经网络预测结果更为准确。该预测方法、结果为交通管理部门提供指导，实现交通事故向预防性转变，达到道路交通安全的目的。
