引言
目前，垃圾焚烧发电厂的数量及垃圾平均处理规模日益增加，焚烧技术在我国的垃圾处理领域越来越具有重要地位[1]。2000年建设部发布了我国垃圾处理的政策，对于现行的垃圾焚烧技术具有重要指导意义，其中指出：宜采用炉排炉技术进行垃圾焚烧。实践证明炉排炉技术确实是现阶段最适宜的垃圾焚烧技术。
炉排炉焚烧控制技术包含焚烧炉炉膛温度控制、出口氧量控制、给料炉排速度控制、翻动炉排滑动炉排控制、助燃风量控制，其中多个控制环节需要利用垃圾料层厚度作为控制条件，所以垃圾料层厚度的软测量对于垃圾焚烧来说具有重要意义。
通过前人对垃圾焚烧软测量的研究可以总结出：料层厚度计算容易受助燃风机风量或风压大幅度变化的影响；一次风压与垃圾阻力、炉排阻力呈线性关系；利用一次风流量、风室和炉膛压力可以反映出垃圾厚度。
垃圾料层厚度在实际应用中，采用划分等级可满足控制要求。因此，本文利用现有料层厚度计算方法结合现场运行人员经验，划分出料层厚度等级。然后建立自适应模糊神经网络(Adaptive Neuro-Fuzzy Inference System，ANFIS)料层厚度模型，采用最小二乘法和误差反向传播算法对模型参数进行学习，最终实现对炉排料层厚度的测量。
1 垃圾料层厚度计算
对于料层厚度的测量，可采用物位计进行测量。超声波物位计与雷达物位计是两种主流物位传感器。理论上可以准确测量出炉排表面的料层厚度，但由于该设备为单点测量设备，现场物位计安装位置不同，炉排表面垃圾凹凸不平，厚度不断变化，测得的料层厚度只是局部料层厚度，不能反映出炉排整体料层厚度值，同时炉膛内扰动因素较多，测得厚度与实际厚度偏差较大，现场使用效果并不理想。同时，焚烧过程产生的高温环境不利于上述物位的长期稳定运行。
因此，目前主流方法为间接测量法。通过达西定律结合Klinkenberg现象，得到干燥段垃圾厚度计算[2]公式：
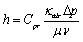
式中，
—焚烧炉特性系数
—空气渗透率
—炉排上下方差压
—空气粘度
—空气渗流速度
—垃圾料层厚度
该公式为垃圾料层厚度软测量提供了理论依据。因此，传统炉排上方垃圾厚度可以由炉排下方风室的压力与炉排上方压力作差得到，其计算原理见图1。
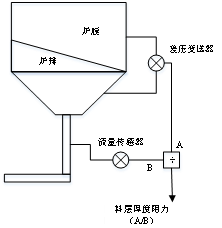
图1 垃圾焚烧炉排炉料层厚度计算原理
将公式(1)简化后，得到现有垃圾厚度阻力计算公式[3]如下：
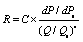
式中：
——料层厚度阻力信号;
c、n——常数，由垃圾热值决定;
——炉排上下方差压，Pa;
——炉排上下方差压经验值，Pa;
——干燥风流量，Nm3/h;
——干燥风流量经验值，Nm3/h；
本文该公式使用前提，，则可认为c、n值保持不变，具体取值如表1所示。
表1 垃圾料层厚度计算公式部分输入参数取值
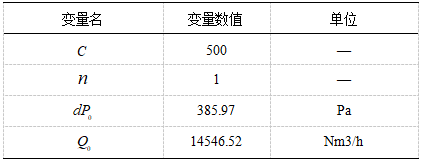
公式（1）中固定值参数取值如上表所示。
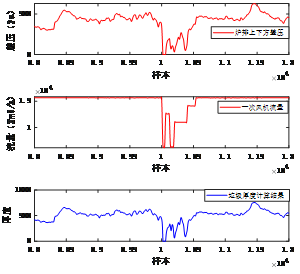
图2 垃圾焚烧炉排炉料层厚度公式计算结果曲线
从上图可以看出，一次风机的大幅度变化，会造成炉排上下方差压的大幅度变化，从而导致料层厚度计算的大幅度波动，对相关控制的稳定性极其不利。
2 ANFIS模型
自适应模糊神经网络(ANFIS, Adaptive Network-based Fuzzy Inference System)是一种将模糊逻辑和神经网络结合的一种模糊推理系统结构，既发挥了二者的优点，又弥补了各自的不足。
J-S.R.Jang提出的自适应神经模糊推理系统是一种将模糊逻辑和神经元网络有机结合的新型的模糊推理系统结构，采用反向传播算法和最小二乘法的混合算法调整前提参数和结论参数，并能自动产生If-Then[4]规则。
ANFIS是一种基于Takagi-Sugeno模型的模糊推理系统，它将模糊控制的模糊化、模糊推理和反模糊化3个基本过程全部用神经网络来实现，利用神经网络的学习机制自动地从输入输出样本数据中抽取规则，构成自适应神经模糊控制器，通过离线训练和在线学习算法进行模糊推理控制规则的自调整，使其系统本身朝着自适应、自组织、自学习的方向发展。
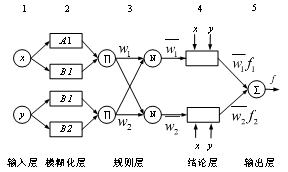
图 3 自适应模糊神经网络结构
假设，模糊神经网络系统具有两个输入x，y,一个输出z，,其结构如图4所示，对于一阶Takagi-Sugeno模糊模型，如果具有以下2条模糊规则：
规则1：
if x is A1 and y is B1 then f1=p1x+q1y+r1
规则2：
if x is A2 and y is B2 then f2=p2x+q2y+r2
ANFIS模型包括五层:输入层、模糊化层，规则层，结论层，输出层[5]。
模糊神经网络模型第一层为输入层，其作用是将输入变量传递到下一层。
第二层为模糊化层，负责输入信号的模糊化，本文采用高斯函数作为函数，其表达式如下：
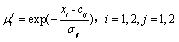
（5）
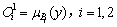
（6）
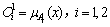
（7）
第三层为规则层，每个节点都表示一条模糊规则，完成对模糊逻辑的‘与’[6]操作，之后对上个节点的结果进行归一化。
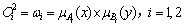
（8）
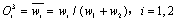
（9）
第四层为结论层，其输出如下：
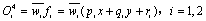
（10）
第五层为输出层，其输出如下：
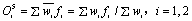
（11）
基于ANFIS的垃圾料层厚度软测量模型，具体建模流程见图。
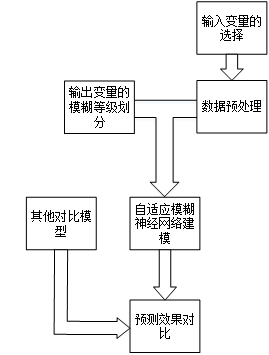
图4 垃圾焚烧炉排料层厚度模型设计流程
3.1 数据预处理
采集垃圾发电厂运行数据，采样间隔为1s。先对数据进行滤波、去除坏点等处理。将处理后的数据每60s取一个均值，共得到9000组数据，8500组数据作为训练集，500组数据作为测试集。
3.2 垃圾料层厚度软测量模型输入变量选择
由公式(1)可知，计算垃圾厚度需要知道一次风粘度、炉排上下方差压以及一次风流速。垃圾料层厚度计与炉排上下压差与流速的比值有关[7]，而流速又可以通过流量计算得出，一次风粘度又与风温有关。因此，最终确定如下五个变量作为炉排垃圾厚度阻力预测模型输入：
1)一次风机风量；
2)炉排上下方差压；
3)一次风温；
4)炉排上下方压差与一次风流量之比。
3.3 输出变量划分等级
垃圾厚度软测量计算模型的输出由模糊语言的形式来表示。垃圾厚度模糊等级由现有公式结算结果结合专家经验给出。根据垃圾厚度的高低，模糊子集分为{负极大，负大，负中，负小，零，正小，正中，正大，正极大}，或者可以表示为{NB,NM,NS,ZE,PS,PM,PB}，对应数字等级为1-7。
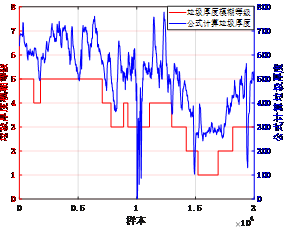
图 5 料层厚度公式计算值与模糊等级对比
3.4 建立自适应模糊神经网络
模糊神经网络输入隶属度函数个数太少，输出准确度较低；输入隶属度函数个数太多，会导致需要训练参数过多，系统训练速度过慢、模糊规则过多。为此，通过大量实验，分别调整五个输入的隶属度函数个数，在满足精确度要求的前提下，尽量减少隶属度函数个数。逐个增加每个输入变量的隶属度函数个数，得出其误差，最终确定，三个输入的隶属度函数个数分别为10,10,5，10，对比各种隶属度函数类型，经过实验，采用高斯函数作为输入隶属度函数时，精确度最好，公式如下：
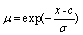
（12）
式中，c与
分别为高斯隶属度函数的中心和宽度。
训练次数为100,采用BP算法和最小二乘估计法的混合算法来进行学习[8]，提高训练速度。
4 实验结果及讨论
最终，得到的输入的隶属度函数如图6所示。
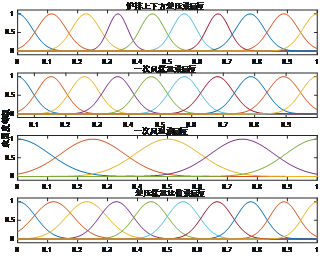
图 6 自适应模糊神经网络输入隶属度函数（放在结论里面）
为了验证ANFIS模型在实际料层厚度预测中的准确性，对图8所对应时间段内的料层厚度进行预测，结果如下图：
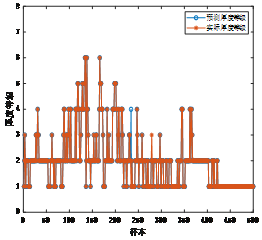
图 7 ANFIS模型料层厚度模型预测效果对比
统计ANFIS模型预测值与实际值，可得出模型预测准确率为99.4%。
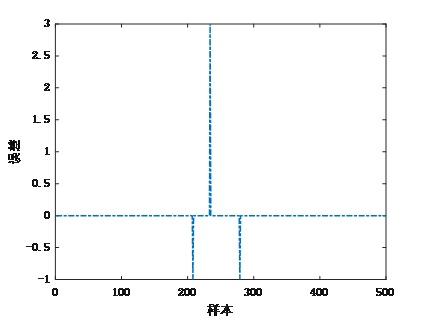
图 8 ANFIS模型预测值与实际值误差
从图7可以看出，ANFIS模型料层厚度预测等级与专家经划分等级基本保持一致，能够较为准确反映出当前料层厚度，图8表明，ANIFS模型具有较高的预测准确性。
5 结论
由于垃圾料层厚度在垃圾焚烧发电实际过程中并不需要十分准确的数值，因此采用划分等级的方法，既能够满足控制要求，又可以避免厚度计算值波动严重造成给料炉排等系统控制稳定性变差。
自适应模糊神经网络模型建模简单，精度高，具有一定的可靠性，能够定性反映出垃圾料层厚度的实际值。基于自适应神经网络垃圾料层厚度软测量模型，，利用分级思维结合神经网络实现对料层厚度的描述，既结合了现场运行人员积累的经验，又结合神经神经网络的学习能力，在一定程度上为垃圾焚烧发电控制提供了新方法。
