2017年12月,普通高中新修订课程方案与课程标准颁布,凝练了各学科核心素养,提出了学业质量标准,数学学科将“学生发展为本,立德树人,提升素养”作为基本课程理念之一。在课程标准提出的六个核心素养中,数学建模具有独特的地位,数学模型搭建了数学与外部世界联系的桥梁,是数学应用的重要形式,是应用数学解决实际问题的基本手段,也是推动数学发展的动力,对培养学生用数学眼光观察世界、用数学思维思考问题、用数学语言表达交流,提高发现问题、提出问题、分析问题、解决问题能力具有重要意义。
一、数学建模的基本概述
著名数学家怀特海曾说:“数学就是对于模式的研究”。
所谓数学模型,是指对于现实世界的某一特定研究对象,为了某个特定的目的,在做了一些必要的简化假设,运用适当的数学工具,并通过数学语言表述出来的一个数学结构,数学中的各种基本概念,都以各自相应的现实原型作为背景而抽象出来的数学概念。各种数学公式、方程式、定理、理论体系等等,都是一些具体的数学模型。举个简单的例子,二次函数就是一个数学模型,很多数学问题甚至实际问题都可以转化为二次函数来解决。而通过对问题数学化,模型构建,求解检验使问题获得解决的方法称之为数学模型方法。我们的数学教学说到底实际上就是教给学生前人给我们构建的一个个数学模型和怎样构建模型的思想方法,以使学生能运用数学模型解决数学问题和实际问题。数学建模主要表现为:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题。随着数学知识的深入学习,学生的知识积累程度,学生对于数学建模的理解程度,这些方面都会不断地提升,想要进一步提升学生的数学建模能力,要对数学建模有持之以恒的态度。高中数学建模最简单的解释就是利用学生们学习过的理论知识来建立数学模型解决遇到的问题。数学建模的基本过程就是对生活中或者课本中比较抽象问题解决的过程。
二、数学建模的主要步骤
数学建模的步骤主要包括以下三点:(1)前期的准备工作。在数学建模的前期,要积极地运用数学语言来描述问题,要根据实际对象的特征以及建模的目的等不断对问题进行必要的简化,此外,在具体的教学中,教师要有意识、有目的地引导学生,带领学生理解建立数学模型的基本思路。在高中数学的学习中,学生会接触诸多模型,比如函数模型、不等式模型以及几何模型等,这些基础知识能够帮助学生解决实际问题。(2)尝试建模。前期准备工作做好之后,就可以利用适当的数学工具来建立相应的数学结构。在具体教学中,教师可以带领学生完成一些不太复杂的问题,比如储蓄问题、贷款问题等,这些应用能带给学生一些数学建模的初步体验。(3)主动探究。模型并不一定是准确、合理、适用的,它需要人们将模型分析结果与实际情况进行对比,如果模型与实际较为吻合,那么就可以清楚地解释计算结果,相反的,如果模型与实际不相符合,那就需要再次重复建模的过程。
三、数学建模的有效策略
1.创设问题情境,建立数学模型
问题能够激发学生的探究兴趣,唤起个体课堂求知欲,驱动他们对未知知识的探究.数学建模围绕问题情境展开课堂教学,促使高中生以合作形式来展开探究,以发展个体建模能力。在新课改指导下,高中数学教师要结合日常实际来为学生创设问题情境,从他们学习出发点,在真实问题情境中发展数学思维。
如,在“等差数列与等比数列”教学中,教师结合生活实际来创设问题情境,即,植树节要到来了,班里同学积极参加义务植树活动,其中第一名同学种植了一棵树、第二名同学种植了两棵树、第三名同学种植了三棵树,直到第n位同学种植了n棵树,其中1≤n≤50,那么,班里总计种植了多少棵树.借助于真实问题情境,学生从题干材料中找到已知和未知条件,结合学习到的新知识,探讨运用数学要素来建立数学模型.在问题情境中,学生在问题中应用等差数列求和公式解答问题,建立数学模型来求解正确答案,形成数学素养。
2.注重生活实例,激发学习兴趣
传统数学教学中,教师往往重视抽象知识讲解,忽视了数学与实际有机联系。随着新课改的深入发展,数学课堂倡导数学与实际相结合,贯彻数学思想,与生活联系来开展数学课堂教学活动。数学建模过程有助于高中生理解数学教材,全面思考和掌握教材中概念、公式和定理等內容,贯通教材与生活的联系,从而把真实生活问题转换为数学问题,实现建模思想在高中学习中的内化,形成数学建模思想。
如,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域BCDE为休闲游乐区,AB,BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度)。∠BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=3 km。
(1)求道路BE的长度;
(2)求道路AB,AE长度之和的最大值。
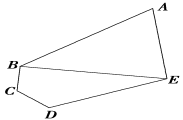
[思路点拨] (1)连接BD,由余弦定理可得BD,由已知可求∠CDB=∠CBD=30°,∠CDE=120°,可得∠BDE=90°,利用勾股定理即可得BE的值。
(2)设∠ABE=α,由正弦定理,可得AB=4sin (120°-α),AE=4sin α,利用三角函数恒等变换的应用化简可得AB+AE=4sin (α+30°),结合范围30°<α+30°<150°,利用正弦函数的性质可求AB+AE的最大值,从而得解。
3. 构建建模意识,培养概括能力
教师应研究在各个教学章节中可引入哪些模型问题,如讲立体几何时可引入正方体模型或长方体模型把相关问题放入到这些模型中来解决;又如在解几中讲了两点间的距离公式后,可引入两点间的距离模型解决一些具体问题,而储蓄问题、信用贷款问题则可结合在数列教学中。要经常渗透建模意识,这样通过教师的潜移默化,学生可以从各类大量的建模问题中逐步领悟到数学建模的广泛应用,从而激发学生去研究数学建模的兴趣,提高他们运用数学知识进行建模的能力。
数学运用能力是数学教学中的薄弱环节,因此提高学生数学运用能力是提高数学素养的关键,在实际教学中一要重视概念的演变过程教学。使学生弄清数学概念的发生、发展过程,二要开展模型教学及数学建模能力训练。这样,学生就会在不断的学习中逐渐从实际问题中培养出出色的抽象能力,进而概括能力也会大幅度的得到提高。
结束语
综上所述,要提高中学生解决数学问题的能力,就要让学生学会简化数学问题,理清数据之间的关系,简言之就是培养学生学会运用数学建模解决问题。老师上课的时候尽量用学生熟悉的事物和题目进行结合,在学生都觉得数学通俗易懂的情况下,达到降低中学数学建模教学难点的目标。我们相信,在开展“目标教学”的同时,大力渗透“建模教学”必将为中学数学课堂教学改革提供一条新路,也必将为培养更多更好的“创造型”人才提供一个全新的舞台。
参考文献
[1] 梁振强.高中生核心素养之“数学建模”能力的培养与思考——以“建立数列模型解决实际问题”教学为例[J]中学数学研究(华南师范大学版),2019(4)。
[2]延伟红.递进式建模教学,提升学生核心素养[J].中学数学教学参考,2019,(10):16-18。
[3]郑大鹏.数学建模在高中数学课堂的教学策略研究[J].数学教学通讯,2017(04):45-46。










