一、数学建模以函数为基石，以立体图形为背景
例1（2017新课标Ⅰ理16. 5分）如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形。沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥。当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为_______．
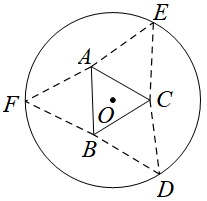
【素养落地】试题用函数方法解决立体几何中最值问题，体现了几何问题代数化，以导数为工具解决了优化问题，提升了考生的直观想象、数学建模及数学运算素养。
【建模试题考查特点】本题包含数学建模中建立模型和求解模型两个过程，借助已有数学建模的结果得到目标函数，再用导数法求最值，解决了实际问题。属于数学建模水平一层次。
例2．（2011江苏17，14分）请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm
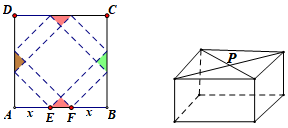
（1）某广告商要求包装盒侧面积S（cm2）最大，试问x应取何值？
（2）某广告商要求包装盒容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．
【素养落地】试题属于函数模型的选择和应用，利用体积公式构建包装盒容积公式，再用导数法求最值。试题考查数学建模能力、空间想象能力、数学阅读能力及解决问题能力。试题提升了数学建模、直观想象、数学运算素养。
【品赏】
1.知识的覆盖上：以立体图形为模型，考查了函数概念与性质、导数等基础知识，也考查了数学建模能力、空间想象能力、数学阅读和应用能力。
2.题目的取材上，设计包装盒，体现试题源于生活，服务于生活，源于教材，高于教材，有所创新，体现学以致用的宗旨。
3.试题的设计上，加强应用意识，体现现实联系实际。
二、数学建模以三角为背景，与函数深度融合
例3．（2018江苏14分）某农场有一块农田，如图所示，它的边界由圆O的一段圆弧MPN（P为此圆弧的中点）和线段MN构成．已知圆O的半径为40米，点P到MN的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为△CDP，要求A,B均在线段上，C,D均在圆弧上．设OC与MN所成的角为θ．
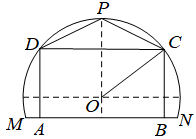
(1)用θ分别表示矩形ABCD和△CDP的面积，并确定sinθ的取值范围；
(2)若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．
【素养落地】试题为三角函数大题，考查了解三角形的应用问题，也考查了构造函数以及利用导数求函数的最值问题。本题侧重考查运算求解能力及应用意识，提升了考生的数学抽象、数学建模、数学运算素养。
【建模试题考查特点】本题经历了数学建模的建立模型、求解模型、完善模型过程，能够在关联的情境中，理解数学建模的意义，能够用模型的思想说明问题。考查数学建模水平二层次。
三、数学建模以日常生活为情境，凸显应用意识
例4．（2018上海14分）某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时，某地上班族S中的成员仅以自驾或公交方式通勤，分析显示：当S中x%(0<x<100)的成员自驾时，自驾群体的人均通勤时间为
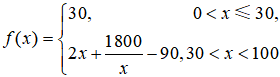（单位：分钟），
而公交群体的人均通勤时间不受x影响，恒为40分钟，试根据上述分析结果回答下列问题：
(1)当x在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？
(2)求该地上班族S的人均通勤时间g(x)的表达式；讨论g(x)的单调性，并说明其实际意义．
【素养落地】试题以生活实际为背景，构造了分段函数模型，体现了数学的实用性。从实际问题提炼数学模型，解决数学模型回到实际问题中检验。本题对函数的要求较高。试题考查数学阅读能力及应用意识，提升了考生的数学建模、数学抽象、数学运算素养。
【建模试题考查特点】本题能够在熟悉的实际情境中，模仿学过的数学建模过程解决问题。能够在关联的情境中，经历数学建模的过程，能够运用数学语言，表述数学建模解决问题的过程和结果，用模型的思想说明问题。本题考查数学建模水平二层次。
例5(2020全国1卷理3.5分)．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为
解析：D
数学建模素养，与其他核心素养：数学抽象、逻辑推理、直观想象、数学运算、数据分析深度融合，渗透到高考中的每一道应用题。为了应对新高考，课堂教学中应该以核心素养为主线，以函数为载体，将数学建模素养落到实处，落实到每一节课，每一道题，让高中课堂教学从题海战术跳出，注重学生从“解题”到“解决问题”能力的培养，逐渐形成核心素养。另外，数学建模素养，能够对其他素养起到辐射作用。所以，数学建模素养的养成，势在必行。
通过近几年高考题的研究，数学建模素养的考查，渗透在代数与几何的各个板块，均属于小题或大题压轴。能力与素养并重，求活求新，这将是未来高考压轴题的一大趋势。所以，数学建模这个课题研究，对于 “培优”工程，起到举足轻重的作用。
参考文献：
1.《高考真题卷》
2.《普通高中数学课程标准》（2017版）
