1工程背景
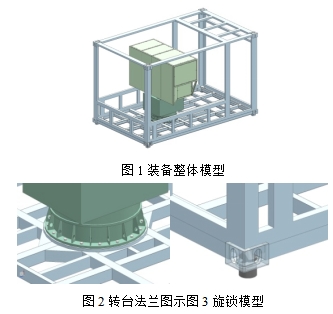
某舰载装备为集装箱型式,4m的箱内安装大型转台,转台通过底部法兰盘与箱体底板螺栓连接;整个箱体通过集装箱标准旋锁固定在甲板上。在不考虑箱体蒙皮及活动门窗的情况下,装备的三维模型见图1~图3。
根据GJB150.23A-2009的规定,该装备在海上的倾斜/摇摆指标要求见表1。
表1倾斜/摇摆指标要求
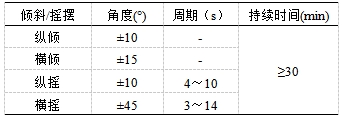
倾斜摇摆指标在试验时采用倾斜摇摆试验台实现。纵倾/横倾是指试验台绕其横轴/纵轴旋转,并停止在规定角度位置静止不动;纵摇/横摇是指试验台绕其横轴/纵轴以规定周期进行往复摇动,属于动态过程考核。分析以上指标可知,横摇时,其角幅值最大,且摇动周期下限值最小,故仅从受力角度考虑,在横摇时装备受力最严苛,需着重分析横摇状态下装备的受力影响。
2原理分析
建立横摇时的力学模型,如图4所示。
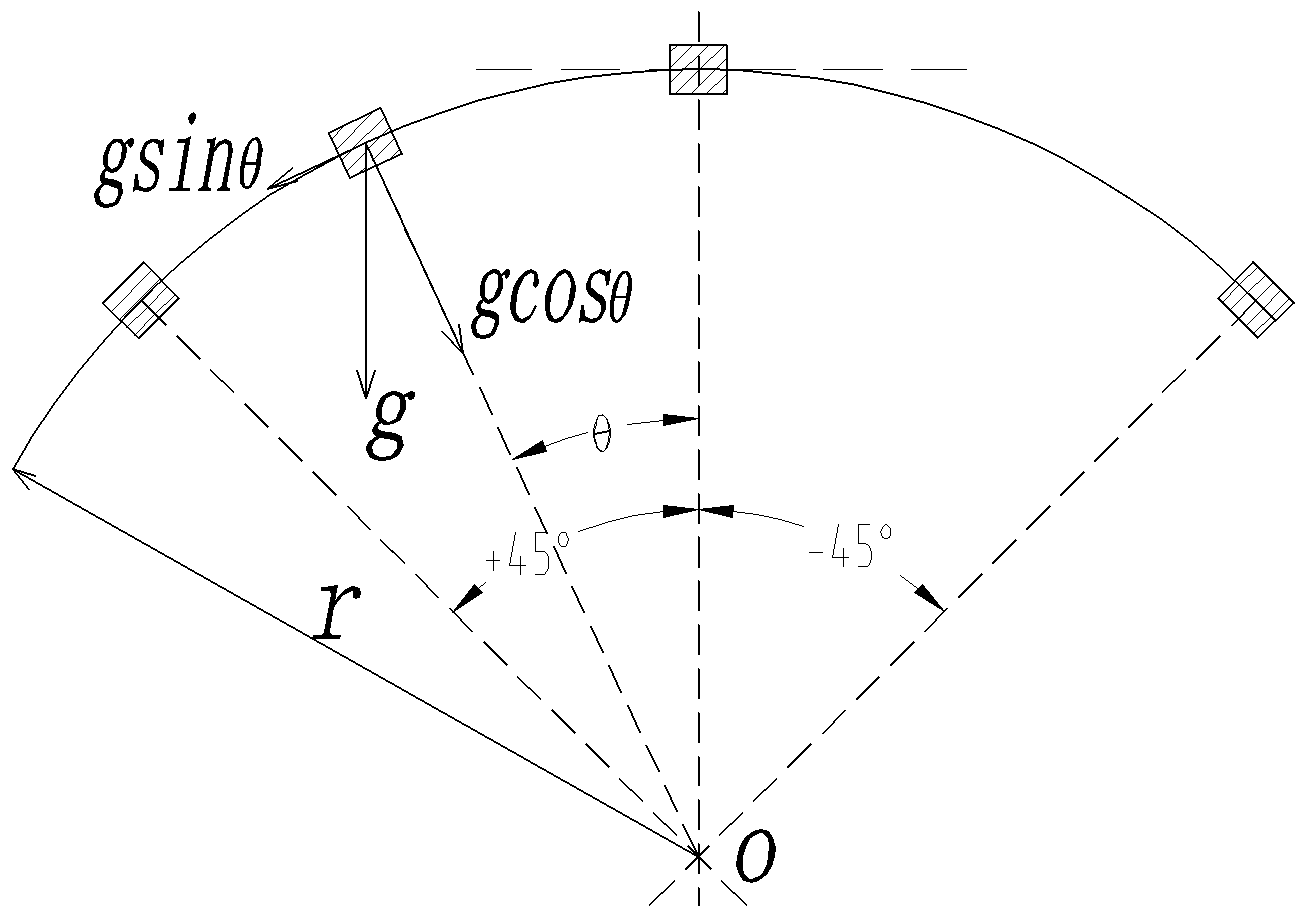
图4受力模型
其中θ为横摇角度,r为横摇时的转动半径,g为重力加速度。摇摆周期T=3s。固定周期的往复横摇运动可用正弦曲线模拟,即θ=Asinωt。
对角度函数进行一次求导和二次求导,分别得到角速度和角加速度表达式:θ′=Aωcosωt;θ″=-Aω2sinωt。
横摇时,已知几个过程点的时间-角度对应关系见表2。
表2时间-角度对应关系
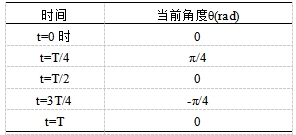
故可知摇动角度函数θ=Asinωt中,A=π/4rad,ω=2π/3rad/s。
更进一步,考虑重力加速度影响,横摇状态下,合成向心加速度an和合成切向加速度at的表达式为:
an=θ′2×r+gcosθ
=(Aωcosωt)2×r+gcos(Asinωt);
at=θ″×r-gsinθ
=-Arω2sinωt-gsin(Asinωt)。
通过以上分析:
(1)横摇状态下,考虑安装结构强度时,主要威胁为新产生的切向加速度at,对安装根部产生额外的切向应力;
(2)横摇半径影响切向加速度at的大小,即r值越大,at值越大;
(3)角速度θ′及角加速度θ″可作为进一步有限元分析的运动载荷施加在分析模型中。
3算例验证
利用ANSYSWorkbench分析软件进行仿真分析,通过在软件中设计简单算例,验证上一章节原理分析推导的加速度与实际运动仿真结果的一致性。
(1)算例模型
算例模型如图5所示,底板与上端质量块通过中间的细梁连接,连接处设置为绑定接触,材料及其属性选择软件中的默认值。在摇摆状态下,下端连接部位为薄弱环节,预计将出现应力最大值。
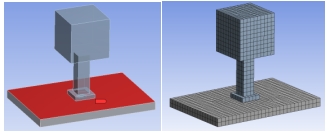
图5算例模型
(2)仿真分析
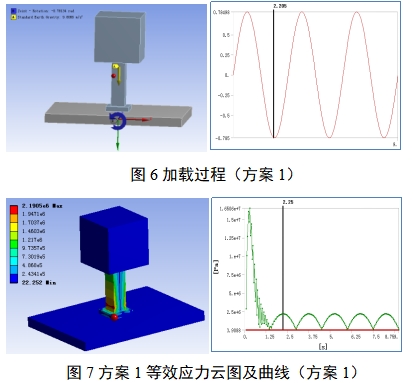
方案1:建立瞬态分析过程,通过建立转动副,施加角度驱动,使算例模型绕底板横轴摇动。该方案直接模拟摇摆的动态过程,最为直接。向转动副施加角度的时间历程表达式,即θ=Asinωt,摇动角幅值A=π/4rad,摇动角速度ω=2π/3rad/s,同时加载重力加速度,设置时间历程为9s(即3个摇动周期)。加载过程如图6所示,通过求解提取等效应力结果如图7所示。
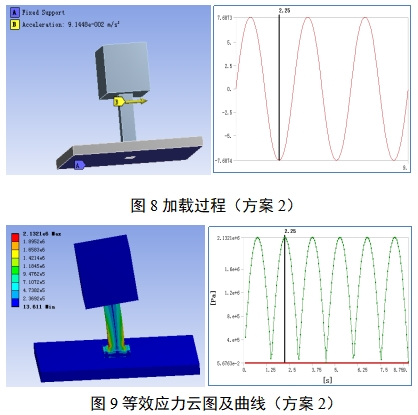
方案2:建立瞬态分析过程,根据第2章节推导的摇动运动过程,可将摇动运动的力学特征等效为切向加速度载荷,即固定底板,向模型施加横向加速度载荷at,设置时间历程为9s(模拟3个周期)。加载过程如图8所示,通过求解提取等效应力结果如图9所示。
方案3:通过在静力结构分析中,向模型施加切向加速度峰值,求解静态情况下,峰值加速度作用时的应力,与方案2进行比对,加载过程及应力云图如图10所示。

(3)结果对比
通过以上3种方案计算后,模型的等效应力对比见表3。
表3结果对比
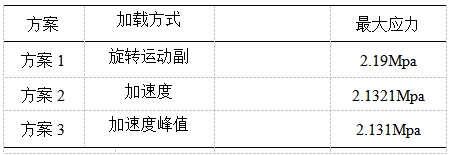
方案2和方案3的结果基本一致,这是因为:通过模态计算算例的一阶固有频率约171Hz,而外界激励频率约0.3Hz,频率比很小,响应传递函数接近1,系统能力无复集,在该激励下响应不会放大,故方案2瞬态加速度峰值的力学响应可等效为稳态静力加速的力学响应;
通过算例,主要对比方案1和方案2结果,可以看出,通过两种加载方式,计算结果基本一致,相互印证,即原理分析的切向加速度值正确,且对于此类摇动运动,有限元计算时,既可以通过施加切向加速度求解,也可以通过施加转动副驱动,直接求解;
本简单算例的验证,为下一章节实际问题的求解、分析打下基础。
4、实际问题求解、分析
在实际问题中,根据已知条件,按照算例中方案2的加载方式,模拟实际运动过程,通过求解,校核结构设计强度。
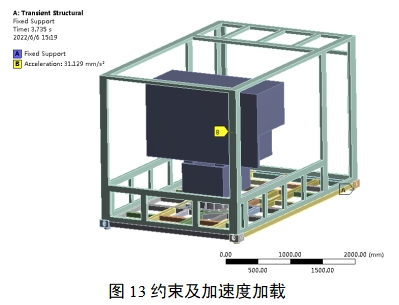
仿真模型:针对实际需要,在仿真计算时,只考虑转台与箱体底部连接强度,忽略转台体内部的连接强度分析(转台体内部连接强度分析由转台体设计时保证)。转台体中间部位及上端舱体简化模型,刚性连接,通过等效质量法赋密度后,模拟真实状态。
箱体底板及转台下半部分法兰安装处根据实际工程设计完整建模,网格划分后如图11所示,网格数量为523847个。

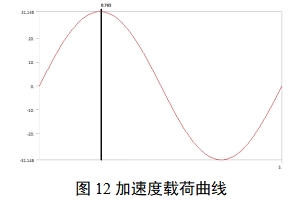
施加载荷:建立瞬态分析,为减小计算时间,取时间历程3s(即1个摇动周期),固定四角旋锁,向模型施加横向加速度载荷,加速度载荷表达式为:at=Arω2sinωt+gsin(Asinωt),旋转半径根据实际装载舰船情况取7m,加载曲线如图12所示。
计算求解:通过计算,提取等效应力云图,如图14所示。时间历程的等效应力大小如图15所示,最大应力出现在箱体底板法兰安装盘周围,最大值约228Mpa(出现在2根方管连接端面,可认为是应力集中点,其余主要承力部位应力值约100Mpa左右),位移云图如图16所示,最大位移出现在转台顶端,约13mm。
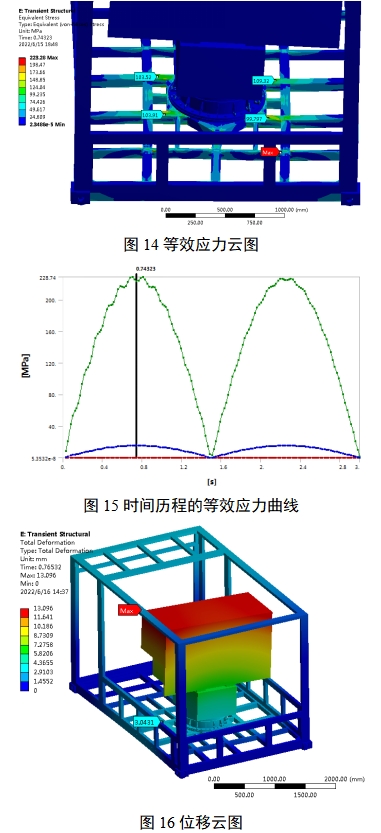
结果分析:通过仿真分析,箱体底板在转台安装周围应力相对较大,但小于底板骨架材料Q345管材的屈服强度345Mpa,底板不会发生破坏,但由于转台上端未约束自由度,下端的变形通过自身放大,导致上端变形达13mm,故有必要对底板应力集中区域进行强化设计,减小应力,同时控制基础变形,减小转台上端的变形量。
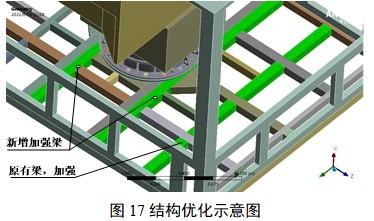
结构优化:根据上述仿真计算结果,安装法兰所在的2个横向梁进行加强,直接在原有位置处向外扩展新增2根梁的布置,同时对原应力集中的辅助梁进行加强,矩管截面由80×40×3mm,改为80×80×4mm。模型如图17。
对优化、加强后的模型,施加原有约束条件及载荷,进行求解计算,应力分布如图18所示,位移云图如图19所示。
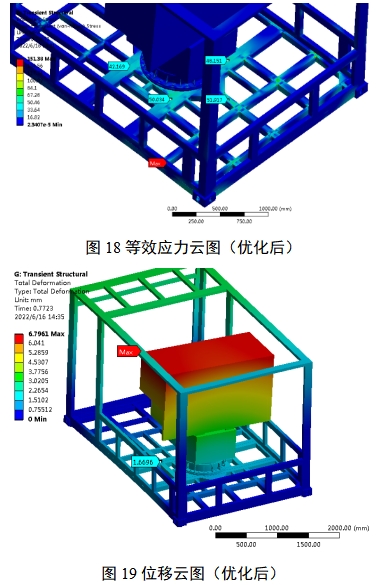
加强后,底板应力最大值降低至约为151Mpa,出现在箱体底板与侧板连接矩管的端面,仍可认为是应力集中点,安装法兰所处的2根主要承载梁上应力降低至50Mpa左右,应力状况有明显改善,同时底板上的变形降低至约1.6mm,转台顶端变形降低至6.7mm左右,即结构的优化加强起到明显效果。
4、总结
全文从实际问题出发,对舰载装备在横摇运动下的力学特征进行了原理分析,并通过在有限元软件中建立简单算例,对理论分析结果进行验证,同时获取了横摇运动仿真分析的两种加载方案。
再进一步根据原理分析及验证结果,对实际问题进行了求解校核,分析了该装备连接部位的结构强度,根据求解结果,对连接部位的结构设计进行了优化加强和效果比对。全文的分析过程及结论,可以作为此类型问题的重要参考。
参考文献:
[1]倪剑,周勇.倾斜摇摆对船用转子受力影响的研究[J].中国重型装备,2018.
[2]军用装备环境试验设备倾斜摇摆试验台校准方法[J].计量、测试与校准,2020.
[3]朱刚,杨晓伟等.倾斜摇摆试验台校准技术研究[J].宇航计测技术,2018.
[4]黄国强.舰载机武器系统倾斜及摇摆试验方法探讨[J].航空标准化与质量,2012.
[5]GJB150.23A-2009军用装备实验室环境试验方法第23部分:倾斜和摇摆试验[S].总装备部军标初版发行部,2009.
作者简介:
王锐锋(1987-),男,汉族,陕西宝鸡,硕士研究生,工程师,从事集成设计与相关技术研究。










