0 引言
随着我国社会经济的飞速发展,为了提高通行效率及经济的更好的快速发展,道路、桥梁及隧道等基础建设也越来越多,由于受到地形的限制,需要挖填方,各种各样的边坡也越建越多。受到各种人为因素或者自然因素的影响,一些边坡出现失稳的现象,危害公众的生命财产安全,山体自然边坡一旦出现滑坡灾害现象,给人带来的损失是巨大的,边坡的安全性受到越来越多的关注。
本文借鉴了刘航雨等对围岩力学参数对小净距隧道初期支护受力影响的研究思想,利用MidasGTS有限元计算软件,建立二维边坡模型,计算不同边坡力学参数下的边坡稳定安全系数,采用控制变量的方法分析均质边坡各个力学参数对安全系数影响大小。
1 有限元分析软件
有限元的原理是将结构离散化,将结构划分为有限多个单元,施加边界诶条件,再进行一系列刚度矩阵、柔度矩阵及位移矩阵的迭代计算。
本文采用的右线元分析软件为Midas GTS。Midas GTS主要用于进行岩土的数值建模分析计算,它前处理和后处理都采用全界面的可视化操作,有简单直接的优点,内部有丰富强大的材料库,能满足大多数的岩土材料情况,获得的结果也较为偏于安全。在计算边坡的稳定安全系数时,用Midas GTS岩土有限元分析计算软件的边坡安全系数计算模块(SRM)计算,能自动搜索出安全系数最小即最危险的滑动面,利用强度折减法计算出边坡的安全系数。
2 有限元强度折减法
分析边坡安全性中,有限元强度折减法相对于极限平衡法有着明显的优势:有限元软件能自动搜索最危险滑动面,相比极限平衡法手算假设滑动面更方便且更准确;有限元强度折减法考虑了边坡的应力与应变的相互作用;有限元强度折减法还能计算一些较为复杂的边坡的安全系数。
有限元强度在进行边坡稳定性分析的方法是按照折减的步长,逐渐降低边坡岩土体的一些力学参数,直到边坡出现破坏特征,将边坡破坏时折减的系数作为边坡稳定安全系数。具体的方法是,在边坡稳定分析中,将岩土体的粘聚力c和内摩擦力φ的正切值除以折减系数F,其他岩土力学参数保持不变,从而得到一组新的岩土力学参数,再进行有限元计算,根据破坏判定依据,若判定此时边坡失稳破坏,则该系数F即为边坡的安全系数,若根据判断依据,未能达到破坏标准,则增大F的值再进行有限元计算,直到用判定依据判定边坡失稳破坏。计算公式如公式(1)和公式(2)所示。
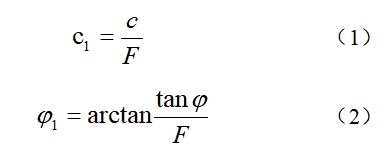
强度折减法中判定边坡失稳破坏的标准主要有数值模型有限元计算不收敛、边坡塑性区贯通及滑动面上的位移与应变将产生突变,产生很大的且无限制的塑性流动三种。每种判定方式得到的结果也有差异,Midas GTS中使用的判定依据是第一种计算不收敛。
3 模型参数
3.1 模型尺寸参数
利用Midas GTS建立二维实体边坡模型,模型试验中所有模型的坡高均为20m,为尽量减小尺寸效应的影响,模型左右边界到坡脚及坡顶的距离均取3倍坡高即为60m,下边界到坡脚的距离为2倍坡高即为40m,坡角β除第一组坡角试验以外均为45°。边坡模型具体参数设置如图1所示。
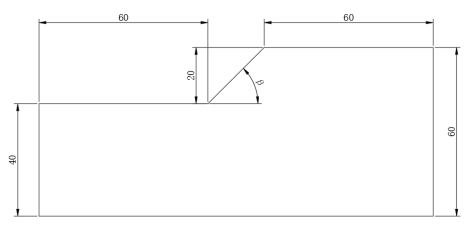
图 1 模型尺寸
3.2 各力学参数对边坡安全系数影响对比
将各组结果绘制在同一张图中,对比分析各个参数对边坡安全系数影响的程度。如图2所示。
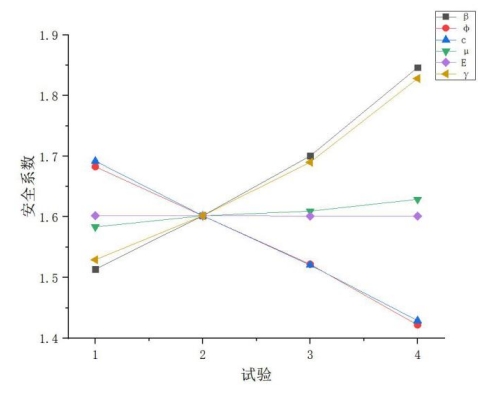
图 2 各力学参数对边坡安全系数影响对比
由图2可以看出边坡岩土体的弹性模量和泊松比改变数值,仅引起安全系数的小幅度变化,表明弹性模量和泊松比对边坡安全系数的影响很小;粘聚力和内摩擦角对应的两条线,变化趋势相同,都接近线性,且程度很相近,图形几乎重叠,表明对边坡安全系数影响程度基本一致;坡角和重度对应的两条线,变化趋势相同,与内摩擦角和粘聚力变化趋势相反,图形也很接近,表明对边坡安全系数影响程度接近。
4 结论
利用控制变量法的方式设置边坡力学参数,建立右线模型,分别计算出各自情况下的安全系数,通过分析不同参数变化给安全系数带来的变化,在本文的试验条件下得出以下结论:
(1)弹性模量和泊松比对均质边坡安全系数的影响近似,影响都很小。
(2)粘聚力和内摩擦角对均质边坡安全系数影响程度基本一致,随着粘聚力或内摩擦角的减小,安全系数呈线性减小,粘聚力或内摩擦角的减小10%,安全系数减平均小5%左右。
(3)坡角和岩体重度对安全系数影响相近,随着坡角或重度的减小,安全系数增大,影响程度较大,略大于粘聚力和内摩擦角的影响程度。
参考文献
[1] 刘航雨,陈寿根.围岩力学参数对小净距隧道初期支护受力影响的研究[J].路基工程,2020:135-138.
[2] 帅红岩,韩文喜,赵晋乾.Midas/GTS软件在边坡三维稳定分析中的应用[J].地质灾害与环境保护,2009,20:104-107.
[3] 赵尚毅,郑颖人,时卫民,王敬林.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002:343-346.
[4] 罗堂,何超亮.强度折减有限元法在边坡稳定性分析中的应用研究[J].福建建设科技,2020(03):63-64.
[5] 毕小勇,闫天俊,鲁杰.Midas-GTS(SRM)在边坡二维稳定性分析中的运用[J].自然灾害学报,2015,24(01):170-176.
[6] 闫佐菲,曾令强.重力作用下顺层岩质边坡破坏机理数值模拟研究[J].矿产与地质. 2020(01):124-126
[7] 杨明财,盛建龙,翟明洋,董舒.基于应力状态法的某岩质边坡稳定性分析[J].化工矿物与加工: 2017:11-14.










