1软件无线电接收机原理及结构
根据Nyquist采样定理,高频模拟信号经过数字ADC采样后,在数字域形成一定的频谱结构,采样后的数字信号表示为XD(f)。接收机的主要目的是从XD(f)中提取出感兴趣的基带信号s(n)。由于任何一种调制信号都可以用幅度、相位和载波对应的函数来表示,所以信号s(n)可表示为:
![]() (1)
(1)
式中,A(n)、ω0、θ(n)分别为信号的幅度分量、载波分量和相位分量。对式(1)进行三角函数正交分解,得到s(n)的正交表达形式为:
![]() (2)
(2)
式中:
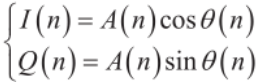 (3)
(3)
式(2)称为基带信号的两个正交分量,即同向分量和正交分量。载频ω0主要用于信号频谱搬移,不携带信息,所以调制信号s(n)完全可以由两个正交分量来表征。接收机的主要作用是从载波处提取这两个正交分量,在频谱不失真的前提下进行数据流降速处理后输出给后续解调模块。如图1所示,混频器产生正交的两路信号,低通滤波器Hi(ejω)主要滤除I(n)和Q(n)频谱分量以外不需要的信号,以消除邻道干扰的影响。经过接收机提取后的正交分量信号I(n)和Q(n)已经变为基带信号,假设其带宽为B,由于B≤fs/2,因此可以对正交分量I(n)和Q(n)进行抽取。设抽取值为D,则D可表示为:
![]() (4)
(4)
满足式(4)关系的信号抽取不会改变原频谱结构,信号不会失真。抽取后的信号可以表征原始信号,但数据速率降低为之前的1/D,大大减轻了后续基带处理模块的数据处理能力要求。例如,fs=200MHz,B=25kHz,则根据式(4)可得D=2000。这样在对相同信号进行处理时,基带处理模块的数据处理速度可以降低2000倍。基于低通滤波的软件无线电接收机如图1所示。低通滤波器和后接的各级抽取器构成了一个标准的抽取系统,用于降低后续处理模块速率的处理要求。
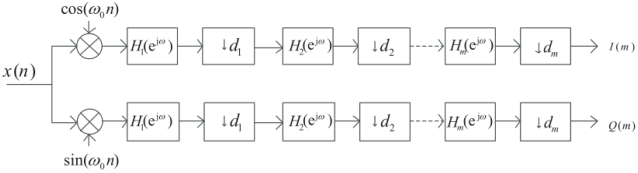
图1基于低通滤波的软件无线电接收机结构
图1共采用了M级抽取,每一级的抽取因子分别为Dm,总的抽取因子为:
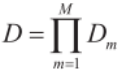 (5)
(5)
该结构可以有效降低后级处理模块运算速度要求,但由于滤波器数据输入端处在抽取器之前,滤波器需要提供高速运算能力,特别是在高速取样率情况下,前级滤波器将面临很大的数据处理压力,对处理器是一个大的挑战,不利于实时性和稳定性要求高的系统。由图1可知,滤波器输入速率最高处在第一级,也就是前级需要提供较高的数据运算能力。针对软件无线电接收机前级速率要求高的特点,本文提出了一种改进的接收机结构,即基于多相滤波的软件无线电接收机结构,如图2所示。这种结构将前级滤波器改用多相滤波结构来实现。多相滤波器运用子滤波器并行运算的特点,在满足总的运算速度要求前提下,可以降低子滤波器速率要求,从而在高速取样率情况下有效取代低通滤波器,解决硬件运算能力不足的问题,有效提高接收机的实时处理能力,同时提升硬件运行稳定性。
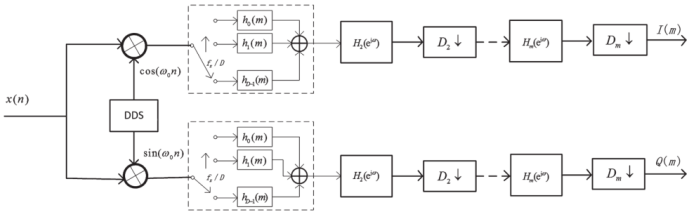
图2基于多相滤波的软件无线电接收机结构
2低通整数倍抽取
软件无线电接收机结构中低通抽取器的主要作用是对基带正交信号数据流进行降速,且不改变信号频谱结构,目的是降低后续基带处理模块数据处理要求。多速率信号处理整数倍抽取是其基本理论基础,因此深入理解和掌握整数倍抽取理论对软件无线电各种接收机结构都至关重要。
整数倍抽取是将高速采样序列x(n)每间隔D-1个数据选取一个样点,得到一个新低速序列xD(m),即:
![]() (6)
(6)
抽取序列的离散傅里叶变换为:
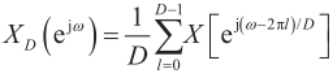 (7)
(7)
由式(7)可知,抽取后的低速序列频谱XD(ejω)为原高速序列频谱X(ejω)经过2π周期频移和D倍频谱拓展后叠加而成。在频谱频移和拓展的过程中频谱会发生混叠,这时需要先对原始高速序列频谱进行滤波,滤除带宽π/2(D=2)以外的信号,然后进行2倍抽取,使得抽取后的低速序列不会发生频谱混叠,且可以准确表征原高速序列感兴趣频谱部分。
这样抽取后的低速序列频谱XD(ejω)可以准确表示原高速序列频谱X(ejω),后续基带处理模块只需提供较低的数据处理能力,就可完成对原始信号的等同处理。它的数据速率只需高速序列时的1/D,大大降低了对后续基带处理模块处理速度的要求。
结束语
通过计算及仿真对比可知,相对于低通抽取结构,该结构计算要求降低1/D2,同时大大降低了滤波器累积误差,提高了计算精度,在实时性要求高的场合是一种高效的解决方案。该结构已成功运用到30~108MHz频段射频直采某设备,采用ADI公司的某ADC芯片,采样速率fs=250MHz。接收机模块采用Xilinx公司的Zynq-7000系列FPGA实现。
参考文献
[1]樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2017:176-248.
[2]杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001:17-110.










