引言:数学建模是高中数学的核心环节,有助于帮助学生解决数学难题,激发创新性思维。关于高中数学核心素养,旨在保障学生主体性地位基础上,激发自主性学习,既促使学生养成良好的思维习惯,又提高学生学习能力和综合素质。函数模型在高中数学中占据大量篇幅,需要教师充分发挥引导作用,搭建好函数模型基础,促进学生建模能力和学习能力提升,这对于学生成长及发展至关重要。
1 数学建模概述
数学建模,是指对现实问题的抽象性分析,采用数学语言搭建模型、从而解决问题,整合建模搭建过程成为处理数学与客观世界联系的纽带,在数学应用中发挥着关键性作用[1]。关于数学建模的过程,教师应充分发挥引导作用,整合利用教学内容,实际数学课堂上,遵循趣味性原则、适度原则、可操作原则基础上,围绕学生主体性地位,观察情景、发现问题、数据收集,构建模型、解决问题。比如,以高中数学中函数知识点为例,需要运用函数构建模型解决实际问题主要有以下步骤:
(1)观察情景:结合实际生活,发现问题的演变过程。
(2)发现问题,分析内在变量关系和逻辑关系,包括常量、变量等相互性和适用性特点。
(3)数据收集:收集和整理数据,分析数据变化过程,明确具体的运动变化数量及类型。
(4)构建模型:整合数据内容,搭建函数模型,从数学视角出发,有针对性地处理“数学性”的实际问题。
(5)解决问题:一是求解函数模型,根据相关数据运算推理,逐步解析函数模型;二是检验模型,深刻分析解实际问题的规律性,实现解决相关类型问题的过程。
2 高中生数学建模能力培养策略(以高中函数为例)分析
2.1 保障学生主体性地位,创设轻松愉悦的学习氛围
高中函数教学,教师首先要做到保障学生主体性地位,创设良好教学情况,不断活跃和谐融洽气氛,实现学生探究式学习。其次,教师应禁忌传统教学思维,革新教学理念,重新审视知识结构,及时查找不足和改正,引导学生主动性学习;在数学课堂上,教师应与学生创建良好的情感关系,增进交流互动,共同讨论结题思路。最后,根据学生的兴趣爱好和心理特点,采取兴趣入学的方法,引起学生强烈好奇心和求知欲,若是有学生主动提出想法和建议,给予学生适当鼓励,转换多种结题思路和方法,确保函数知识的多样性和选择习性;若是学生存在知识误区,禁忌一味地批评和指责,而是教师学会容忍歧义,根据学生各抒己见后,消除学生中的异类做法[2]。
针对高中数学建模,应以解决实际问题为出发点,逐步提升学生理解能力。为有效地解决生活中实际问题,创设日常环节,高效对接函数模型联系性。例如,提出“已知是一城市绿化园林(正方形)面积,求加该园林边长”。学生对问题解读后,老师将学生分成若干讨论小组,使运用回顾指数函数、对数函数等知识,采取类比方式,促进师生共同探讨幂函数定义,从而得出改题计算公式![]() 。
。
2.2 创设问题情景,增强学生思维意识
教师应结合函数教材内容,创设问题情景,以此激发学生思维意识。第一,教师应合理把握教学进度,灵活运用函数素材,创建“问题链”,指引学生带着问题学习。第二,函数模型构建和学习过程中,教师要尊重学生个体差异性,为满足学生个性化发展,需要运用分层教学法,围绕各类学习水平学生,函数学习薄弱环节学生打基础,中等学生重点解决函数模型构建重难点问题,具有一定学习能力的学生有意识地激发创新性思维,教师经过创设层次分明的问题情况,促进所有学生函数学习中知识层面的稳扎稳建。第三,教师要不断加强自身建设,在学生群体中树立良好模范,使学生做到互帮互助,切实形成函数建模思维解决生活中的实际问题。
实际函数模型构建的讲解,在数学课堂上,教师根据学生的学习情况,应以吸收巩固为基本点,循序渐进地推进素质教育,既要指导学生学习新理念、新方法、新思路[3],又应让学生稳扎稳打原有函数模型构建知识的吸收和巩固,根据问题导向,鼓励学生调试和转换模型,从而得到更加精准的数据。也就是说,学生数学建模能力培养,需要长期的累积,这是一个良性循环的过程。比如,结合不同实际问题,需要综合运用各种函数建模方法,根据三角函数应用知识,教师创设以下问题:海水受到引力影响,出现潮汐现象,包括早潮和晚潮,通常船只在涨潮会驾驶到巷道,靠近船坞,待到卸货结束和落潮时反馈返回海洋,其中该港口呈现出的某季水深变化情况,详见表1。
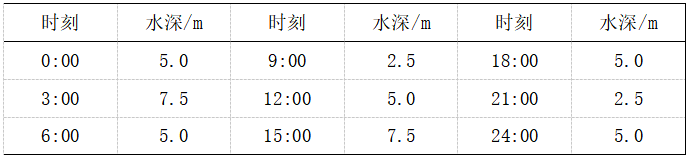
表1 该港口某季节水深变化统计
在本题中,可以根据直角坐标系,定位这几组有序实数的点及位置,从而得出与函数公式![]() 相符,根据前面5个点,整合数据后,从而不难发现
相符,根据前面5个点,整合数据后,从而不难发现![]() ,所以得出
,所以得出![]() ,师生还可以探讨其他思维方向的解题思路。
,师生还可以探讨其他思维方向的解题思路。
2.3 注重思想引领,研究自主式、探究式学习法
教师应根据函数教学,特别是模型构建上,根据学生已有的知识基地,注重思想引领,使学生转被动为主动,实现学生的自主式、探究式学习。一是要总结教学规律,鼓励学生探究式学习,采取概括、类比等方式,观察学生整个自我的思维结题过程。二是根据各类教学法优势及价值,实现对课堂中函数知识讲解的弥补,巩固学生函数知识,提升学习水平和创新意识。三是教师应结合学生课堂表现情况,既要做好新旧对比、注重学生体验,又要强化讨论过程、丰富函数模型构建逻辑认证,期间教师要不断反思,知识总结课堂中问题及不足,促进学生学习水平和创新能力的深化提高。
数学教师为培养学生学科意识和核心素养,在数学模型构建上,应以回归问题为落脚点,考虑到各问题条件及要素不同,对此应强化对模型的盐酸,及时查看结果数据准确度,尤其是判断是否贴合实际。教师应深入渗透数学模型构建,严格遵循“教师为主导、学生为主体”原则[4],科学选取建模素材,运用多样化数学方式,促进学生综合发展。
结束语:数学建模在提升和发展高中生学科核心素养中尤为重要,教师应引导学生结合实际问题,增强数学性思考意识,优选建模素材,创新教学方式方法。数学教学过程中,关注学生整体学习情况,采取因材施教方式,锻炼和培养学生数学交流和解决问题能力。
参考文献:
[1]彭乃霞,谢辉,徐大刚.高中数学建模素养培育的教学案例分析——以人教版(A)数学必修4三角函数模型之"货船进出港时间问题"为例[J].兴义民族师范学院学报,2019,25(2):8.
[2]吴必元.高中数学建模素养培育的教学案例分析——以人教版(A)数学必修4三角函数模型之"货船进出港时间问题"为例[J].数学学习与研究,2020,18(20):2.
[3]刘庆利.布卢姆教育目标分类学指导下的高中数学学科核心素养之数学建模研究——以\"函数模型及其应用\"为例[J].中国数学教育:高中版,2019,15(3):7.
[4]钟三明.核心素养导向下的高中数学建模教学设计——以《三角函数模型的简单应用》一课为例[J].中学数学研究(下半月),2019,17(003):P.25-27.










