一、研究背景
随着计算思维的提出,国内外的教育者便将对人才培养的重点转移到对计算思维能力的培养上。2022年,我国教育部颁布的《义务教育信息科技课程标准》中,计算思维正式被纳入小学信息科技学科核心素养,可见,小学生计算思维培养具有重大意义。浙摄版五年级信息科技教材Scratch软件的程序模块中、设计者在构思Scratch作品及编写程序的过程中,都需要计算思维的参与,所以,Scratch编程是信息科技课堂中培养计算思维的好工具。然而,该培养方式还存在以下问题:计算机编程仅作为载体使用、讲授式教学占主导地位、以知识技能的学习为主,限制了学生的计算思维发展的潜力。如何有效地培养小学生的计算思维能力,是目前研究的重点。
卡梅隆大学计算科学学院的周以真教授认为,计算思维可以与任一学科内容相结合。[1]阅读文献发现,国外学者也极其重视学生计算思维能力的培养,不断尝试与STEM教育结合,实现跨学科培养计算思维,并取得了优异的效果。2016年,我国教育部发布的《教育信息化“十三五”规划》,强调了信息科技在跨学科教与学中的应用。其中,计算思维与数学学科的交融,让广大教育者看到了计算思维培养的希望。计算思维具有隐性特性,培养难度大,而与数学知识相生相息的、充满趣味的可视化的Scratch编程能让计算思维显性化,为计算思维的培养提供了新途径。基于此,本文设计Scratch与数学融合的课堂教学,以促进小学生计算思维的发展。
二、计算思维
随着信息科技与人们生活结合得日趋紧密,计算思维作为一种独特的解决问题的思维方式,正逐步走出其学科专业领域,成为数字化社会生存的一种普适能力。[2]2006年,卡内基梅隆大学计算机系的周以真教授在国际计算机权威期刊上最先提出了计算思维的概念,她指出:计算思维是通过运用计算机科学中的基本概念,并结合其它科学思维,解决问题、设计系统和理解人类行为的复合型思维活动。[3]随后,很多学者纷纷阐释了对计算思维概念的理解,虽然表述不同,但都指向计算思维的问题解决性,肯定了它的通识价值。[4]
很多学者对计算思维的要素进行提炼,把培养的过程和结果显性化,以指导教学活动的进行。综合国内外相关文献,结合数学思维特征,本文将计算思维分为5个维度:概括思维、分解思维、抽象思维、算法思维、评估思维。[5]
概括思维:能够识别问题或任务的共性,建立通用模式或数学模型,并将其应用到类似问题的解决过程中。
分解思维:将复杂的问题分解成若干个小问题,在逐一解决中获得解决问题的新思路。
抽象思维:剔除无关信息,凝练关键要点,聚焦问题本质,将问题进行简化处理。
算法思维:设计一套解决问题的有序、清晰、最优的指令,支持自动化的解决问题方案。
评估思维:对解决问题的过程、方法和效果进行评价,选择最优方案。
三、 面向计算思维培养的“5E”教学模式的建构
“5E”教学模式是由美国生物科学研究院提出的一中基于建构主义的教学模式,主要包括吸引(Engagemeng)、探究(Exploration)、解释(Explanation)、迁移(Elaboration)、评价(Evaluation)。该教学模式一方面有助于教师教学的连贯性,另一方面能够充分挖掘学生的主体地位,注重学生解决问题的能力。计算思维的培养是在学生的实践过程中发生的,强调学生对知识的主动构建。研究发现,“5E”教学模式对探究能力的提高有积极作用,为计算思维发展提供可能。[6]如,英国伦敦大学学院开发小学数学的编程课程,便借鉴了“5E”理念指导教学,增强教学的连贯性和趣味性,彰显了学科融合对计算思维培养的积极作用,具有很大的实践意义。[7]
鉴于此,本文建立了面向计算思维培养的“5E”教学模式,用于指导ScratchMaths课堂教学,培养小学生的计算思维。
图1.面向计算思维培养的“5E”教学模式
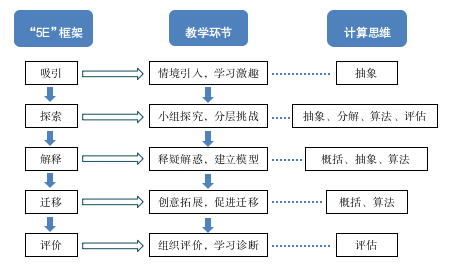
(一)吸引:情境引入,学习激趣
情境认知理论强调知识与学习发生的情境化。情境化的课堂导入是为了吸引学生的注意,调动学生的热情,打开学生的思维。贴近生活、符合小学生认知的情境,能够让学生快速建立知识联接,抽象出学科内容,积极进入学习状态。
(二)探索:小组探究,分层挑战
在该阶段,教师通过设置问题、提供资料等方式,引导学生将复杂的问题或任务分解为若干简单的问题或小任务,由简到难,由浅入深,逐步解决。学生结合所学数学知识,在不断试误中选择最优方案,设计算法,实现解决问题的自动化。这个过程中,教师不仅是教学的组织者、问题解决的引导者,还是困难学生的帮助者,学生分解思维、算法思维、对解决方案的评估思维等得到良好的发展。
(三)解释:释疑解惑,建立模型
学生完成每一个小任务后,将过程及相关数据记录到任务单上。教师鼓励学生梳理过程,分析数据,勇于阐述解决问题的思路和想法,形成对问题或任务的正确认识,抽象出一定的思维模式,在不断尝试中建立通用模式或数学模型,并验证它们的适用性。
(四)迁移:创意拓展,促进迁移
学生在解决问题、完成任务中理解了问题的本质,建立了一般模式。在该阶段,教师可以设置半开放性的挑战任务,一方面检验模式的通用性,在遇到类似问题时能够举一反三,促进迁移,另一方面发散学生的思维,提高学生的创造性。
(五)评价:组织评价,学习诊断
最后,是学生作品展示、评价交流环节。评价分为两个部分,一个是学生根据自我表现的自评;另一个是经过组内成员讨论,选出最优作品进行展示,学生对该小组的作品进行他评。学生在欣赏他人作品和相互交流反馈中,认识自己的不足,完善认知结构,促进思维发展。
四、ScratchMaths课堂教学实践——以《画正多边形》为例
本文分析Scratch相关教学内容,结合与数学学科的契合点,对五年级下册《循环嵌套》进行创编,设计了《画正多边形》一课,探究Scratch编程与数学融合,提高小学生的计算思维能力。
通过本节课学习,学生能够在绘制正多边形的过程中,熟练掌握画笔指令,移动、旋转、重复指令的使用;结合数学特征,有意识地发现规律,总结共性,建立解决问题的一般模式,提升迁移能力;在绘制正多边形的过程中,提高学生的算法优化思想,体验编程的乐趣,养成规范、严谨的编程习惯。
(一)吸引:情境引入,学习激趣
教师活动:课前引入,揭示课题
1.展示图片:建筑物上面的正多边形图案;自然界花朵对称图形。
2.问:你发现了什么?
3.揭示课题:利用scratch绘制正多边形,呈现本课任务:绘制各种各样的正多边形。
学生活动:明确任务,进入状态
1.仔细观察展示的图片。
2.观察图片,说说发现。
3.接收学习任务,打开软件。
(二)探索:小组探究,分层挑战
教师活动一:引导学生分解任务
1.直接绘制正多边形,对大家来说很困难,可以将任务分解成几个小任务逐步完成。请同学们以小组为单位进行交流、思考,怎么一步步完成图案的绘制。
2.请学生说说自己的想法,并进行鼓励和引导。
3.请学生打开“学生挑战任务单”,记录解决问题的思路。
4.展示任务单,及时反馈。如表1。
表1.学生挑战任务单
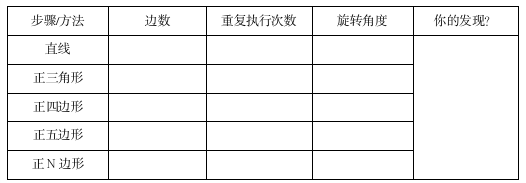
学生活动一:根据引导分解任务
1.思考交流,阐述解决问题的思路,并根据教师或同学的反馈优化思路。
2.将解决问题的方法和步骤记录在任务单上。
教师活动二:巡视反馈,协助指导
表2.教师指导过程表
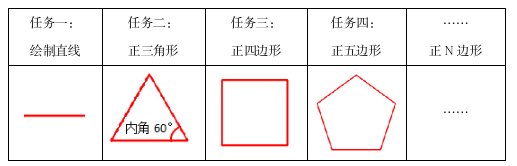
1.绘制直线:教师强调严谨、规范化的脚本。
2.绘制正三角形:
①提示学生使用“左转”或“右转”实现绘制方向的改变。
②请学生说说绘制过程中遇到的困难,引出三角形内外角的概念,理解“左转”或“右转”的是外角。然后让学生说说绘制正三角形的脚本特点,尝试优化脚本,引出“重复执行”指令。
3.绘制正四边形:引导学生使用优化算法编写脚本。
4.绘制正五边形:让成功的学生说说正五边形的外角(旋转角度),若没有同学知道,教师可适当引导学生根据任务单中的数据,找到旋转角度和重复执行次数(边数)的关系(乘积是360°),动画演示,加深理解。如图1。
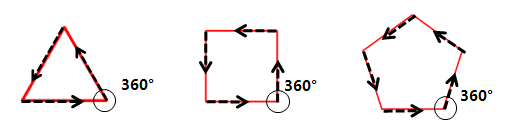
图1.绘制正多边形图示
5.教师关注学生完成情况,统一讲解,个别辅导。鼓励使用不同的方法实现目标。
学生活动二:自主探究,完成任务
1.在Scratch中打开“画正多边形.sb3”文件,设计算法,编写脚本绘制图形。
2.通过思考发现正三角形脚本的特点,在观察和对比中总结规律,优化算法,如图2。
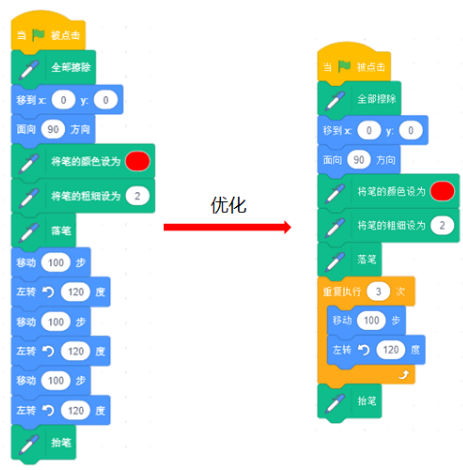
![]()
图2.算法优化程序对比
3.将相关数据记录在“学生挑战任务单”上。
4.观察“学生挑战任务单”中的数据,发现旋转角度和重复执行次数(数)边之间的关系,从而得到正五边形旋转角度(外角)的求解方法。
(三)解释:释疑解惑,建立模型
教师活动:循循善诱,释疑解惑
1.提问:刚才绘制正五边形的时候,旋转的角度怎么得到的?
2.设疑:通过这个方法我们可以绘制任意的正多边形。如果将正多边形的边数设置为变量N,那么旋转角度怎么表示?
3.表扬学生认真思考,积极探索的精神。请学生尝试绘制任意正多边形
4.巡视观察,发现有些学生的正多边形不规则,思考原因。
学生活动:知识重构,建立模型
1.学生举手回答问题。
2.根据教师提示,将零散的知识系统化,总结旋转角度的表达式:360/N,建立绘制正多边形的通用模型,如图3。

图3.绘制正多边形通用程序模型
3.尝试绘制任意正多边形,验证模型的适用性。
4.小组交流讨论,发现正多边形边数越多,图形会越大,除了需要修改重复执行的次数,还要修改移动的步长(边长)。
(四)迁移:创意拓展,促进迁移
教师活动:呈现拓展任务,促进知识巩固
展示拓展任务:绘制多彩多姿的图案,发挥想象力,让图案更惊艳!学生活动:发挥创造潜力,提高迁移能力
根据图案特点,对图案进行创意绘制。
(五)评价:组织评价,学习诊断
教师活动:引导学生进行客观、有效地评价。
学生活动:展示、评价
1.学生展示作品,阐述思路和创意,并说说遇到的困难或需要完善的地方。
2.小组选出最优作品,阐述思路和创意,其他同学欣赏并评价。
五、结束语
作为信息化时代的普适能力,计算思维的培养迫在眉睫。数字化改革之际,传统的“代码式”“工具化”的培养已经远远不能满足社会对高质量人才的需要。面向计算思维培养的编程与数学融合的课堂教学,通过构建“5E”教学模型,促进小学生的计算思维发展,逐渐把学生从“培养成专家”转变为“培养向专家一样地思考的人”,提高学生在数字化环境中的适应能力和创新能力。
参考文献:
[1]马志强,刘亚琴.从项目式学习与配对编程到跨学科综合设计——基于2006-2019年国际K-12计算思维研究的元分析[J].远程教育杂志,2019,37(05):75-84.
[2]李锋.中小学计算思维教育:STEM课程的视角[J].中国远程教育,2018(02):44-49+78-79.
郁晓华,肖敏,王美玲,陈妍.基于可视化编程的计算思维培养模式研究——兼论信息技术课堂中计算思维的培养[J].远程教育杂志,2017,35(06):12-20.
[3]周齐. 支架策略运用在Scratch课堂上对学生计算思维的准实验研究[D].上海师范大学,2020.
[4]缪文溪. 基于计算思维的Scratch编程数学课程的开发与实施研究[D].华东师范大学,2020.
[5][7]陈丽娜. 5E教学模式在小学生计算思维培养中的应用研究[D].内蒙古师范大学,2021.
[6]党建武,曹良政,陈腾飞.面向计算思维培养的5E教学模式实证研究[J].教育信息技术,2022(11):27-30.










