所谓数学综合题是指不仅仅运用数学概念、性质、定理、公式和方法,同时也不局限于数学知识,而是综合运用有关概念、定理和公式,沟通各部分知识和各种数学方法来解决的数学问题。因此综合题一般具有综合性强、思维面广、灵活性大、解题能力要求高等特点,导致解决起来难度大,不少同学往往是见之望而生畏、手足无措,所以提高学生解决数学综合问题的能力显得尤为重要。数学综合题的训练与快速解题恰恰是提高学生综合运用数学知识和思维创新方法的关键所在;寻求解题思路是锻炼数学思维,培养分析能力、创新能力与解决实际问题的能力的有效途径,同时也是素质教育所要培养的各项能力的核心。本文就如何通过初中数学综合问题的求解思路过程来加强创新能力的培养,浅谈几点个人看法。
一、在解综合题中练“三基”
由于综合题涉及综合面广,数学方法多,因此深刻理解数学概念,牢固掌握“三基”(基础知识、基本能力和基本数学思想方法)是求解综合题的根本,也是培养创新能力的前提,夯实基础解综合,解决综合练“三基”,这是求解综合题的立足点。
例1:已知a、b是方程![]() 的两个根求代数式
的两个根求代数式![]() 的值。
的值。
分析:同学的思路是:方法一、由根与系数的关系(韦达定理)得

然后将所求式去括号,(1.1)代入。但由于去括号的式子较复杂,不少同学只好半途而废或运算出错未得结果。

于是原式,解题何等明快,可见夯实基础对解题多么重要。
二、在模仿中求创新
国际数学教育家(美)G·波利亚说过:“当试图解题时,你也必须观察并模仿其他人在解题时的所作所为,并且最后模仿与实践学会解题,进而发展创造性思维,学会创新。”
![]()
分析:此类题目,同学们必定模仿训练过,常规思维方法是先通分,变成同分母分数后,比较分子大小即可,但题中各分数的分母都是质数,通分很繁杂,计算量极大,稍不谨慎就会出错。直觉告诉我们能否寻找其它更简洁的方法,这样想象力有了一个实然的跳跃,产生了一个好念头:在分子相同时,岂不是也可以比较分数的大小?观察本题各分子均为60的因素,答案唾手可得。

三、在迁移中助探索
迁移是十分普遍的科学现象,解综合题毫无疑问理应掌握“迁移术”。在解题中,比较、类比、相似、类似等等都能实现“迁移”,大大有助于猜想、归纳、探索、发展创新思维。

四、在反思中有发现
反思,是解题的重要手段,也是寻觅解题途径的重要思路,反思,可理解为“正难则反”,从问题的反面入手进行思考,也可理解为解题后的再思考,都是在求解综合题时必须积极提倡的。解题实践表明在反思中可以检查出是否有漏解或错解;在反思中可以发现是否有新思路、新解法,乃至拓伸的新命题、新定理,起到触类旁通、举一反三的效果。
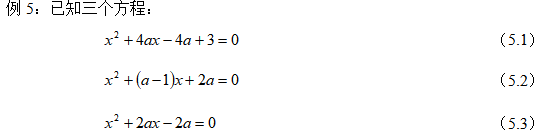
三个方程中至少有一个方程有实数解,求实数a的取值范围。
分析:这是一道常见的综合题,按常规方法,许多同学会模仿性解题:
从已知:“至少有一个方程有实数解”入手,于是分以下7种情况分类讨论:仅方程(5.1)或(5.2)或(5.3)有解;仅方程(5.1)、(5.2)或(5.1)、(5.3)或(5.2)、(5.3)有解;或仅方程(5.1)、(5.2)、(5.3)有解。
诚然,以上求解的思路是常规的,也是正确的,但解题过程将是相当繁琐,略不小心就会导致考虑不周、分类不当或结果漏缺等错误。“正难则反”,求异思维油然而生:从已知:“至少有一个方程有实数解”的反面入手,即3个方程都无实数解,则有:
△1<0,△2<0,△3<0。

巧妙的联想建桥,使一题多解,一图多用,一题多变,多元化的思维方式和解题技巧,都可借助于有效的联想之桥加以实现;联想中领悟出了知识内涵、方法与技巧的内在联系,拓宽了空间解题思路,发展了后天智力,促进了创新能力的培养。
数学综合题的训练与解决是培养提高各项综合能力的核心方法。
【参考文献】:
[1] 汪江松, 曹衍清, 王宪生.高中数学解题方法与技巧[M]。湖北教育出版社。
[2]邓禹绩,肖钰,薛川坪,勒尚成。 初等数学解题思路[M]。海洋出版社。1983年9月。










